数学建模核心模型算法全解：评价模型、预测模型及分类模型等

在数学建模竞赛及各类科研与工程实践中，面对一个具体问题，从纷繁复杂的数据中提炼规律、做出预测或进行评价，其核心环节在于模型的选择与构建。

本文将数学建模中常用的模型算法系统性地梳理为三大范式：评价模型、预测模型与分类模型。每一类模型都对应着不同的研究目的与数据特性。通过阐明其核心原理、数学基础、适用边界与典型应用，并辅以结构化的表格对比，旨在为研究者与参赛者提供一个清晰、全面的“模型工具箱”，帮助大家在面对具体问题时，能够快速、准确地锁定最合适的建模路径。

一、 评价模型：多准则决策与综合比较

评价模型的核心任务是对多个备选方案（或对象）进行系统性比较和排序，从而辅助决策。这类模型通常涉及将多个异质、且可能相互冲突的指标，综合成一个单一的评价分值。其关键挑战在于如何科学地确定各指标的权重，以及如何聚合这些指标信息。

（一） 评价模型的核心流程与选型逻辑

一个完整的综合评价过程，通常遵循“指标体系构建 → 数据标准化 → 权重确定 → 信息聚合 → 排序分析”的逻辑链。选择何种评价模型，主要取决于权重信息来源（主观经验 vs. 客观数据）和信息聚合方式（线性 vs. 非线性）。

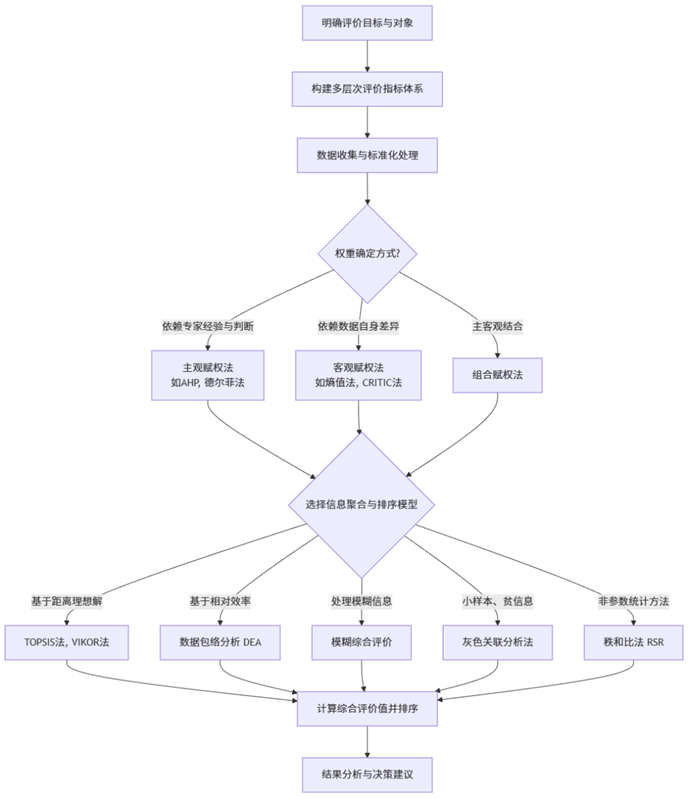
（二） 主流评价模型详解

下表系统梳理了七种核心评价模型，涵盖从经典到前沿的方法。

1. AHP层次分析法

• ‌核心原理与数学思想‌：将复杂问题层次化，通过两两比较构造判断矩阵，利用特征向量法确定权重。
• ‌适用场景‌：决策结构清晰、准则可比较、专家经验重要的战略决策（如项目选址、方案比选）。
• ‌优点‌：系统性强，定性定量结合，易于理解和接受。
• ‌缺点‌：主观性强，因素过多时判断困难，易出现不一致。

2. 熵值法

• ‌核心原理与数学思想‌：基于信息论，指标数据离散程度越大（熵越小），提供的信息量越多，权重应越大。
• ‌适用场景‌：拥有大量客观数据，需完全排除主观干扰的现状评价（如地区发展水平、企业绩效评估）。
• ‌优点‌：客观性强，完全由数据驱动，数学原理严谨。
• ‌缺点‌：忽略决策者偏好，对数据分布和极端值敏感。

3. TOPSIS法

• ‌核心原理与数学思想‌：通过计算评价对象与正理想解（最优解）和负理想解（最劣解）的欧氏距离，进行相对贴近度排序。
• ‌适用场景‌：多属性决策，方案与理想方案差距可度量，追求方案全面优化。
• ‌优点‌：直观合理，充分利用原始数据信息，对数据分布无严格要求。
• ‌缺点‌：无法反映指标间相关性，欧氏距离对指标尺度敏感。

4. 模糊综合评价

• ‌核心原理与数学思想‌：运用模糊数学的隶属度理论，将定性评价转化为定量评价，处理评价中的模糊性和不确定性。
• ‌适用场景‌：评价指标难以精确量化，存在大量模糊语言评价（如教学质量、满意度评价）。
• ‌优点‌：能有效处理模糊、不确定信息，符合人类思维习惯。
• ‌缺点‌：隶属函数确定和合成算子的选择带有主观性。

5. 灰色关联分析法

• ‌核心原理与数学思想‌：通过计算各比较序列与参考序列的几何形状相似度（灰色关联度）来判断其关联紧密程度。
• ‌适用场景‌：“小样本、贫信息”的不确定性系统，数据量少或序列长度不一致（如初期的技术趋势分析）。
• ‌优点‌：对数据要求低，计算简单，适合信息不完全的情况。
• ‌缺点‌：分辨率系数ρ的选择影响结果，对指标权重确定考虑不足。

6. 数据包络分析

• ‌核心原理与数学思想‌：利用线性规划方法，评价具有多投入、多产出的决策单元之间的相对效率，无需预设生产函数形式。
• ‌适用场景‌：评价同质部门（如银行支行、学校、医院）的相对运营效率或效益。
• ‌优点‌：无需预设权重和函数形式，可处理多投入多产出，结果直观（效率值）。
• ‌缺点‌：对异常值敏感，是一种相对评价而非绝对评价，无法有效排序所有有效单元。

7. 秩和比法

• ‌核心原理与数学思想‌：一种非参数统计方法，先将各指标值编秩，再通过秩的线性组合（RSR）进行统计分析。
• ‌适用场景‌：指标无需严格量化，仅需排序；或数据分布不明，需进行非参数综合评价。
• ‌优点‌：方法稳健，对数据分布无要求，能消除异常值影响，可进行分档。
• ‌缺点‌：信息损失较大（仅用秩次），对指标间差异不敏感。

二、 预测模型：基于历史与规律预见未来

预测模型旨在根据已知的历史和当前数据，推断事物未来的发展趋势或具体数值。根据数据特性和内在规律的不同，预测模型主要分为三类：基于时间依赖性的时间序列模型、基于变量间因果/相关关系的回归分析模型，以及从数据中自动学习复杂模式的机器学习预测模型。

（一） 预测模型的选择框架

预测建模的第一步是诊断数据特性：是单变量还是多变量？是否具有明显的趋势、季节性？变量间是线性关系还是复杂的非线性关系？数据量是大还是小？下图展示了基于这些问题答案的模型选择路径。

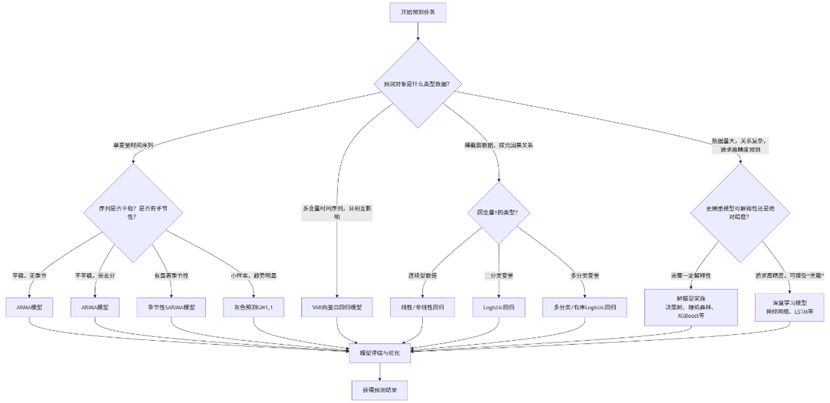
（二） 主流预测模型详解

1、时间序列预测方法

‌（1）ARIMA‌

• ‌核心原理与数学思想‌：将非平稳序列差分后化为平稳序列，再建立ARMA模型。模型记作ARIMA(p,d,q)。
• ‌适用场景‌：单变量、具有趋势但无显著季节性、中等长度以上的序列（如股市价格、产品销量趋势预测）。
• ‌优点‌：理论基础完善，对线性时间序列预测效果好，提供预测区间。
• ‌缺点‌：对非线性模式捕捉能力弱，要求序列平稳，参数识别复杂。

‌（2）季节性SARIMA‌

• ‌核心原理与数学思想‌：ARIMA的扩展，同时考虑非季节性和季节性因素。模型记作SARIMA(p,d,q)(P,D,Q)~s~。
• ‌适用场景‌：具有明显固定周期（如月度、季度）的时间序列（如零售销售额、电力负荷预测）。
• ‌优点‌：能同时处理趋势和季节性，是季节性数据预测的标准工具。
• ‌缺点‌：模型更复杂，参数更多，需要更多数据。

‌（3）灰色预测GM(1,1)‌

• ‌核心原理与数学思想‌：对原始数据累加生成新序列，使其呈现指数规律，建立一阶线性微分方程进行预测。
• ‌适用场景‌：数据量极少（≥4个）、呈现指数增长趋势的短期预测（如新兴技术初期发展预测）。
• ‌优点‌：所需数据量少，计算简单，适用于贫信息系统。
• ‌缺点‌：本质上是指数模型，对波动大、非单调序列预测效果差，长期预测误差大。

2、回归分析预测方法

‌（1）多元线性回归‌

• ‌核心原理与数学思想‌：假设因变量Y与多个自变量X之间存在线性关系，通过最小二乘法拟合最佳线性模型。
• ‌适用场景‌：因变量为连续数值，且与自变量之间存在明确的线性或近似线性关系（如房价与面积、区位的关系）。
• ‌优点‌：模型简单，可解释性强，能检验变量显著性，提供置信区间。
• ‌缺点‌：对线性假设和误差项独立同分布等假设要求严格，对多重共线性敏感。

‌（2）Logistic回归‌

• ‌核心原理与数学思想‌：通过Logit变换将线性回归结果映射到(0,1)区间，用于预测事件发生的概率。
• ‌适用场景‌：因变量为二分类变量（如是/否，成功/失败），预测事件发生概率（如客户流失预警、信用违约预测）。
• ‌优点‌：输出为概率，解释性好，可处理分类问题，是基础的分类模型。
• ‌缺点‌：本质上仍是线性模型，对特征与Logit值间的非线性关系捕捉能力有限。

除此之外还可使用机器学习方法进行预测。

三、 分类模型：从数据中识别模式与归属

分类模型的目标是根据已知标签的训练数据，学习一个分类函数或分类模型，对新的无标签数据进行类别划分。其核心是模式识别。根据学习方式，可分为需要标签的有监督分类（如逻辑回归、SVM）和无须标签的无监督聚类（如K-Means）。

（一） 分类问题建模思路

分类任务始于对数据本身的审视：是否有现成的类别标签？特征的类型（数值型、分类型）是什么？追求的是解释性还是绝对的分类精度？对计算效率有何要求？下图梳理了从问题定义到模型部署的完整思考路径。

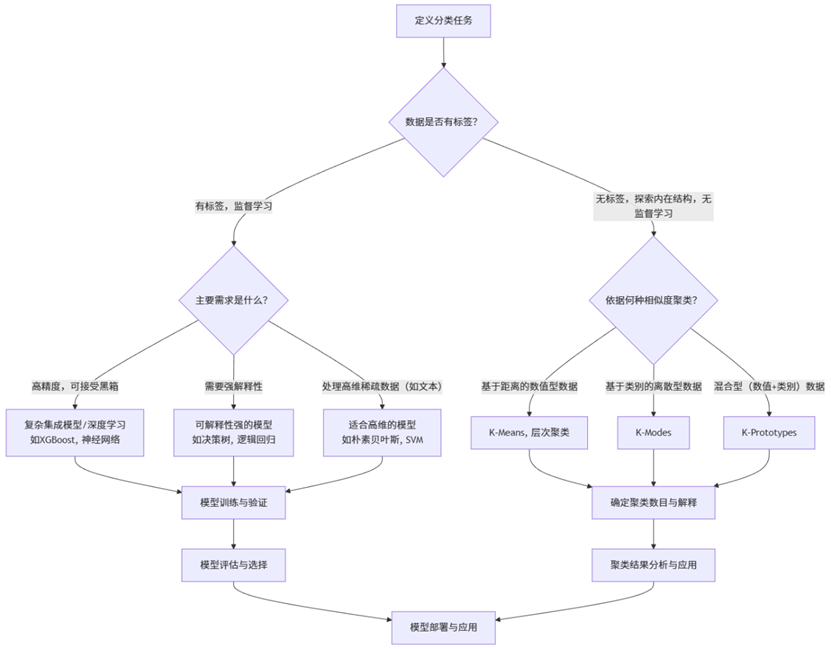
（二） 主流分类与聚类模型详解

下表对比了有监督分类与无监督聚类中的关键模型。

有监督分类方法详解

1. K-近邻（KNN）

• ‌核心原理与数学思想‌："物以类聚"，一个样本的类别由其最近的K个邻居的多数投票决定。
• ‌适用场景‌：样本分布局部特性明显，类别边界不规则，需要惰性学习的场景。
• ‌优点‌：原理简单，无需训练，对异常值不敏感，适合多分类。
• ‌缺点‌：计算量大（需存储所有数据），对高维数据和不平衡数据敏感，K值选择关键。

2. 支持向量机（SVM）

• ‌核心原理与数学思想‌：寻找一个最优超平面，使得两类样本之间的"间隔"最大化，对于线性不可分数据，通过核函数映射到高维空间。
• ‌适用场景‌：小到中等规模数据集，高维特征（如文本分类、图像识别），二分类问题效果尤佳。
• ‌优点‌：理论完备，泛化能力强，尤其适用于小样本高维情况，可通过核技巧处理非线性。
• ‌缺点‌：对大规模训练样本效率低，对参数和核函数选择敏感，多分类需构造。

3. 朴素贝叶斯

• ‌核心原理与数学思想‌：基于贝叶斯定理与特征条件独立性假设，计算样本属于各类别的后验概率，取最大者为预测类别。
• ‌适用场景‌：特征维度高，且特征间相对独立或弱相关的场景（如文本分类、垃圾邮件过滤）。
• ‌优点‌：模型简单，训练和预测速度极快，对小规模数据表现好，适合增量学习。
• ‌缺点‌："特征条件独立"的强假设在现实中往往不成立，影响精度。

无监督聚类方法详解

4. K-Means

• ‌核心原理与数学思想‌：迭代算法，通过最小化簇内样本到簇质心的平方距离来划分簇。
• ‌适用场景‌：数值型数据，已知或可估计聚类数目K，簇呈球状或凸状分布。
• ‌优点‌：原理简单，实现方便，对于大样本集效率较高。
• ‌缺点‌：需预先指定K，对初始质心敏感，对非凸形状和噪声点敏感。

5. 层次聚类

• ‌核心原理与数学思想‌：通过计算样本间的相似度，构建一颗嵌套的树状聚类结构（树状图），可按需在任意层次切割得到聚类结果。
• ‌适用场景‌：不预先指定聚类数，希望得到不同粒度层次的聚类结果，或数据存在层次结构。
• ‌优点‌：无需指定K，可通过树状图可视化聚类过程与结构。
• ‌缺点‌：计算复杂度高（O(n³)），不适合大规模数据，已做的合并/分裂不可逆。

6. DBSCAN

• ‌核心原理与数学思想‌：基于密度的聚类，将簇定义为密度相连的点的最大集合，能识别任意形状的簇，并区分噪声点。
• ‌适用场景‌：数据簇形状不规则，且需要自动识别噪声点和异常值的场景（如地理信息分析、异常检测）。
• ‌优点‌：能发现任意形状簇，抗噪声，无需预先指定簇数目。
• ‌缺点‌：对参数ε和MinPts敏感，高维数据中距离度量失效导致效果下降，不适用于密度差异大的数据集。

四、 总结

本文系统梳理了数学建模中评价、预测、分类三大核心任务的数十种经典模型。以上模型算法均可在SPSSAU中找到并使用，点一点即可完成分析，让没有统计学或者编程基础的同学也可轻松完成数学建模分析。