实验设计的四大神器：从全面试验到均匀设计，理论与SPSSAU实践-优快云博客

一、引言：实验设计的核心使命——效率与智慧的博弈

在科学研究与工业实践中，实验是我们探索未知、优化工艺、改进质量的根本手段。然而，实验资源（时间、成本、物料）永远是有限的。一个核心的矛盾摆在我们面前：如何用尽可能少的实验次数，获得尽可能多、尽可能可靠的信息，从而得出科学的结论？

这就是实验设计（Design of Experiment, DOE）要解决的核心问题。它并非一套简单的实验操作指南，而是一套基于概率论、数理统计和线性代数的科学安排实验方案、高效处理实验数据的理论与方法论。

在面对多因素多水平的复杂系统时，研究者们发展出了多种实验设计策略。本文将深入浅出地对比四种经典且重要的实验设计方法：全面试验、正交设计、响应面设计和均匀设计，并着重介绍后者这一在解决“多因素多水平”问题上展现出巨大威力的“中国智慧”。同时，我们将看到，像SPSSAU这样的现代统计分析平台，如何将这些复杂的设计理论封装成易于操作的工具，赋能科研与工程实践。

二、实验设计方法谱系：四大策略全景透视

为了对各类实验设计方法有一个全局性的认识，我们首先通过下面的流程图来梳理它们之间的关系与选择逻辑：

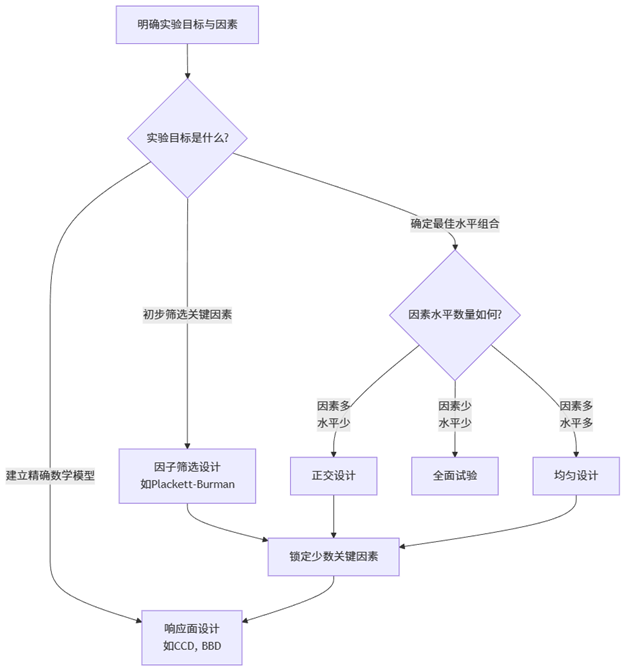
该图谱清晰地展示了不同实验设计方法的定位。接下来，我们将逐一深入剖析。

三、全面试验：基准的荣耀与现实的沉重

3.1 理论基础

全面试验（Full Factorial Design） 是最简单、最直观的实验设计方法。它要求对所有因素的所有水平进行相互组合，构成所有可能的实验条件。

设计公式：如果一个实验有k 个因素，每个因素有n 个水平，那么全面试验的次数N=n^k。
举例：一个3因素3水平的实验，全面试验次数为 3^3=27次。

3.2 优缺点分析

优点：
1. 信息完整：能够获得所有因素、所有水平组合下的全部信息，无一遗漏。
2. 估计精确：可以估计出所有的主效应以及所有因素间交互作用的效应，精度最高。
3. 结果可靠：被认为是评价其他实验设计方法的“金标准”。
缺点：
1. “指数爆炸”灾难：实验次数随因素和水平的增加呈指数级增长。例如，一个5因素5水平的实验，全面试验需要 55=312555=3125 次，这在实际中几乎无法完成。
2. 成本高昂：巨大的实验次数意味着时间、人力和物力的惊人消耗。
3. 效率低下：在很多情况下，大量的实验资源被用于估计那些微不足道的高阶交互效应，造成浪费。

3.3 适用场景

因素数量很少（通常≤4），水平数也较少（通常≤3）的情况。
实验成本极低，可以忽略不计。
作为理论研究的基准，用于验证其他简化设计方法的有效性。

四、正交设计：工业界的功勋元老

为了克服全面试验的“指数爆炸”问题，统计学家们（如英国的R. A. Fisher和日本的田口玄一）提出了正交设计（Orthogonal Design）。

4.1 理论基础

“正交”是一个几何和数学概念，在实验设计中，它意味着实验方案具有均衡分散、整齐可比的特性。

均衡分散：每个因素的不同水平在实验方案中出现的次数相等。
整齐可比：当考察某个因素的水平效应时，其他因素的各个水平会以相同的频率出现，从而使得其他因素的影响相互抵消，使得该因素的效应估计不受干扰。

正交表是正交设计的核心工具，其表达式为LN(mk)，其中：

L：正交表
N：实验次数
m：水平数
k：最多可安排的因素数

例如， L9(34) 表示一个需要做9次实验，最多可以安排4个3水平因素的正交表。SPSSAU操作示例如下图：

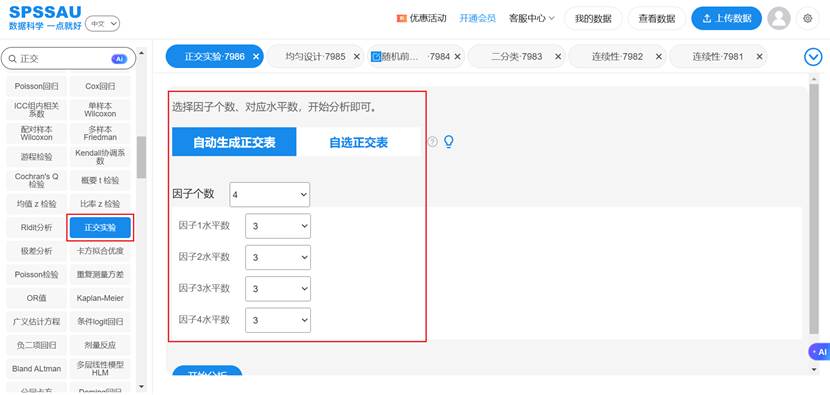
4.2 优缺点分析

优点：
1. 大幅减少实验次数：能从成千上万次全面试验中，选取具有代表性的少数实验（如从27次中选9次）。
2. 数据析出方便：基于正交表的“整齐可比性”，可以方便地用极差分析或方差分析来析出各因素的主效应显著性。
3. 技术成熟，普及度高：在工业界（尤其是质量管理领域）有极其广泛和成功的应用。
缺点：
1. 水平数不宜过多：正交表是预先构造好的，当水平数较多时（如5水平以上），可用的正交表有限，或者实验次数仍然偏多。
2. “嵌套”复杂性：对于水平数不同的混合水平正交设计，表的选择和数据分析稍显复杂。
3. 不适合非线性关系：正交设计主要用于筛选显著因素和寻找最优水平组合，但其设计点通常不足以精确拟合复杂的非线性（如二次）关系。

4.3 适用场景

因素筛选实验，从众多潜在因素中找出少数关键因素。
水平数不多（通常为2-4水平）的多因素实验，寻找最优工艺参数组合。
对实验精度要求不是极端苛刻的工业过程优化和质量改进。

五、均匀设计：中国智慧的“降维打击”

当因素和水平数进一步增加时，正交设计的实验次数仍然显得高昂。针对这一难题，我国数学家方开泰和王元于1978年共同提出了均匀设计（Uniform Design）。

5.1 理论基础

均匀设计的核心思想与正交设计不同。它放弃了“整齐可比性”，而追求实验点在实验范围内“充分均匀地分散”。

均匀性准则：使用数论方法（如好格子点法）或优化算法，生成一套实验方案，使得所有实验点在实验范围内散布得尽可能均匀。衡量均匀性的指标通常是偏差（Discrepancy），偏差越小，均匀性越好。
灵活性：均匀表 UN(mk)UN(mk) 非常灵活，其实验次数 NN 可以等于最大水平数 mm，这使得它能够以最经济的实验次数来应对多水平问题。例如，一个5因素5水平的实验，均匀设计可能只需要5次实验！而正交设计至少需要25次（如 L25(56)L25(56)）。

5.2 优缺点分析

优点：
1. 实验次数极少：这是均匀设计最突出的优点，尤其适合于水平数多（>5）的实验，是解决“多因素多水平”问题的利器。
2. 灵活性极高：几乎可以构造任意因素和水平组合的均匀设计表。
3. 适用于非线性模型：由于点在空间分布均匀，更适合用于建立复杂的非线性回归模型（如神经网络、支持向量机）。
缺点：
1. 失去“整齐可比性”：不能像正交设计那样用简单的极差分析直接判断因素显著性，必须基于实验数据，配合回归分析（通常是多元非线性回归）才能建立模型和优化，对数据分析能力要求更高。
2. 表格选择依赖经验：不同的均匀性准则会生成不同的均匀表，需要使用者根据情况选择。
3. 对模型形式敏感：如果回归模型选得不合适，可能导致结论错误。

5.3 适用场景

计算机仿真实验：在金融、军工、复杂系统模拟等领域，一次仿真计算可能耗时数小时甚至数天，均匀设计能以最少的实验次数探索巨大的参数空间。
化工、制药工艺优化：因素多（温度、压力、浓度、时间等），且需要精细考察水平变化（水平数多）的场合。
新材料配方研究：多种成分的配比优化，水平数通常很多。
任何实验成本极高、周期极长的探索性研究。

SPSSAU操作示例如下图：

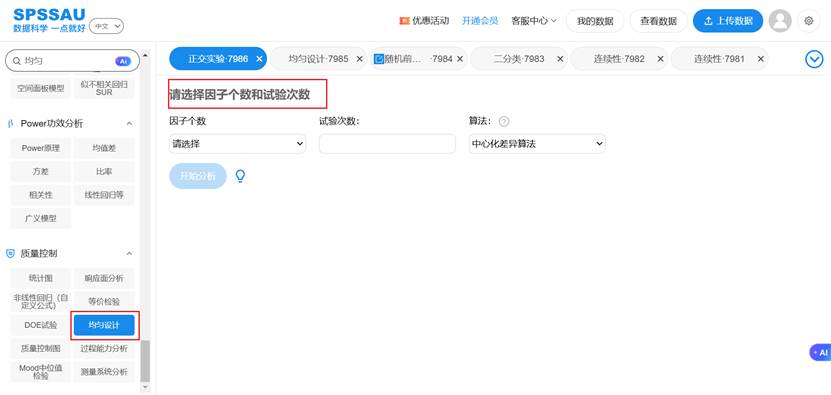
六、响应面设计：精益求精的建模艺术

无论是正交设计还是均匀设计，找到的“最优点”通常只是预设水平组合中的一个。如果我们想精确地找到最优工艺条件，并建立因素与响应之间的定量数学模型，就需要响应面设计（Response Surface Methodology, RSM）。

6.1 理论基础

RSM是一套集实验设计、建模与优化于一体的统计方法。它通过一系列有效的实验，用多项式模型来逼近真实的响应面（一个多维曲面）。

核心设计：最常用的有两种：
1. 中心复合设计（Central Composite Design, CCD）：由立方点（2^k全因子或部分因子）、轴点和中心点构成，可以高效地估计二次回归模型。
2. Box-Behnken设计（BBD）：一种三水平设计，其所有实验点都位于超立方体的棱的中点上，且不在顶点上，适用于实验区域受限的情况。

6.2 优缺点分析

优点：
1. 可建立精确的数学模型：能够拟合非线性关系，揭示因素间的交互作用和平方项效应。
2. 可视化：可以绘制等高线图和响应曲面图，直观地展示因素如何影响响应值，并找到最优区域（峰值或谷底）。
3. 优化功能强大：不仅能找到最优点，还能分析区域的稳健性。
缺点：
1. 因素数量受限：通常只适用于2-5个因素。因素太多，模型会过于复杂，实验次数也会急剧增加。
2. 通常作为二阶段设计：一般是在通过因子筛选设计（如正交设计）找到少数关键因素后，再进行RSM实验，以进行精细优化。

6.3 适用场景

在已确定少数（2-4个）关键因素后，进行工艺参数的精确优化。
需要建立精确的输入-输出数学模型，并可视化分析。
寻找使多个响应指标同时达到最优的折衷条件（满意度函数法）。

SPSSAU操作示例如下图：

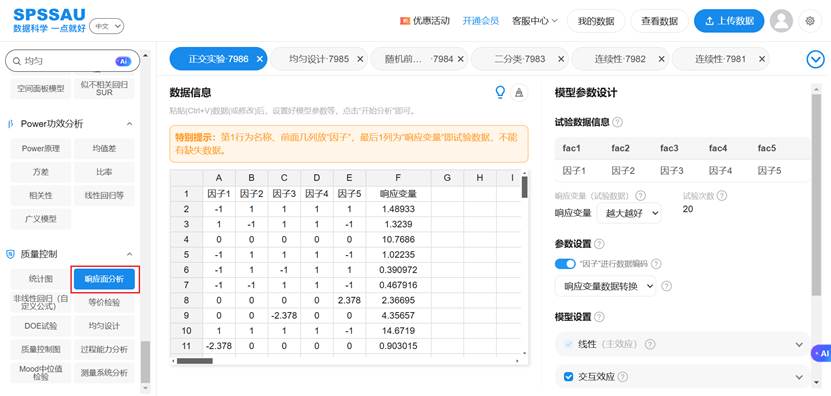
七、SPSSAU在实验设计中的实践价值

面对如此多样的实验设计理论，研究者如何快速上手应用？SPSSAU平台提供了强大的支持：

方法集成：SPSSAU的集成了正交设计和均匀设计等常用方法，用户只需指定因素和水平数，系统即可自动生成最优的实验方案表。
降低使用门槛：无需手动查表，无需理解复杂的数论算法，SPSSAU背后强大的计算引擎为用户完成了最复杂的表格构造工作。
数据分析一体化：生成实验方案后，用户将实验结果录入，SPSSAU可以直接进行后续的方差分析（正交设计）或回归分析（均匀设计），形成从设计到分析的无缝工作流。
教育普及：清晰的结果输出和智能分析建议，极大地帮助了学生和初学者理解和掌握这些重要的实验设计方法。

八、总结与对比

为了更直观地进行对比，我们用一个表格来总结四种实验设计方法的核心特征：

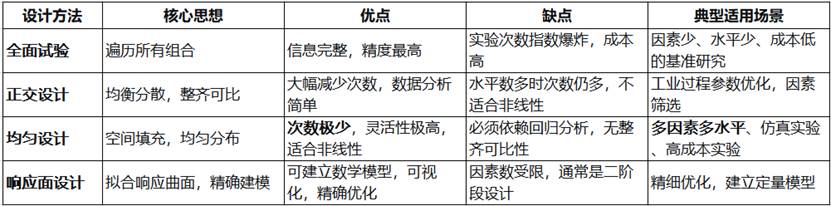
选择策略：

初筛大量因素？用 Plackett-Burman（一种特殊的正交设计）。
因素和水平数适中，找最优组合？用 正交设计。
因素多、水平多，实验成本极高？用 均匀设计。
已有关键因素，需要精确建模和优化？用 响应面设计。

没有一种方法是万能的，优秀的研究者如同一个精通兵法的将军，懂得在不同的战况下，调用最合适的“兵力”（实验设计方法），以最高的效率赢得战争的胜利（解决科学或工程问题）。