时间序列预测全解析：从ARIMA到VAR，理论与SPSSAU实践

时间序列分析是数量研究中最具体系化的方法之一，无论你研究的是宏观经济走势、企业销售预测，还是气象变化、金融波动，其背后都共同依赖于一个核心任务：在时间维度上理解数据，并对未来做出科学预测。

本篇文章将系统介绍常见的时间序列预测方法，包括：ARIMA 模型、季节性 SARIMA 模型、指数平滑（Holt、Holt-Winters）、灰色预测模型（GM(1,1)）、向量自回归模型（VAR）。

一、时间序列预测的基本思想：让过去解释未来

在进入具体模型前，可以先用一张图理解时间序列预测的整体逻辑：

1. 时间序列的三大组成部分

（1）趋势（Trend）

长期上升或下降，例如 GDP、房价、城市人口。

（2）季节性（Seasonality）

周期性波动，例如消费旺季、节假日销售增长。

（3）随机扰动（Random Noise / Error）

无法被模型结构解释的波动。

大部分预测方法其实就是：把趋势 + 季节性 + 自相关结构“拆开、建模、预测”再组合。下面进入正文部分——主流时间序列模型体系化介绍。

二、ARIMA 模型：最经典、最通用的时间序列预测框架

ARIMA模型是时间序列分析领域最重要的基石之一，被称为“时间序列界的线性回归”。

1. ARIMA(p,d,q) 的基本结构

ARIMA 模型本质上由三部分构成：

• AR（自回归）：过去值影响当前
• I（差分）：去除趋势
• MA（移动平均）：过去残差影响当前

数学形式如下（简化）：ARIMA(p,d,q) = AR(p) + I(d) + MA(q)

其思想十分直观：数据不稳定？——做差分（I）；差分后仍有自相关？——用自回归（AR）；误差中仍有信息？——用移动平均（MA）

2. ARIMA 建模流程（Mermaid 图）

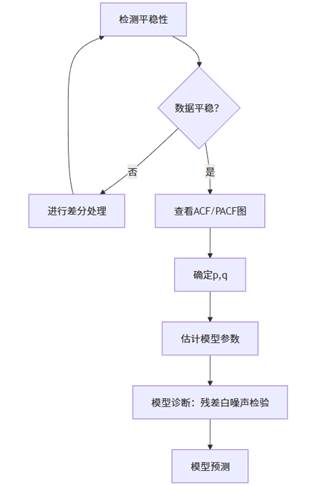
ARIMA 的核心是循环迭代——检查数据是否平稳、差分处理、通过 ACF/PACF 识别 AR/MA 阶数、诊断残差是否符合白噪声要求。只有当残差不再包含可解释信息时，模型才算成功。

在 SPSSAU 中，你只需上传时间序列数据即可自动完成。SPSSAU默认智能地找出最佳的ARIMA模型并且进行预测。如果研究人员自己设置自回归阶数p，差分阶数d值和移动平均阶数q这3个参数，SPSSAU则按照研究人员设置进行模型构建。

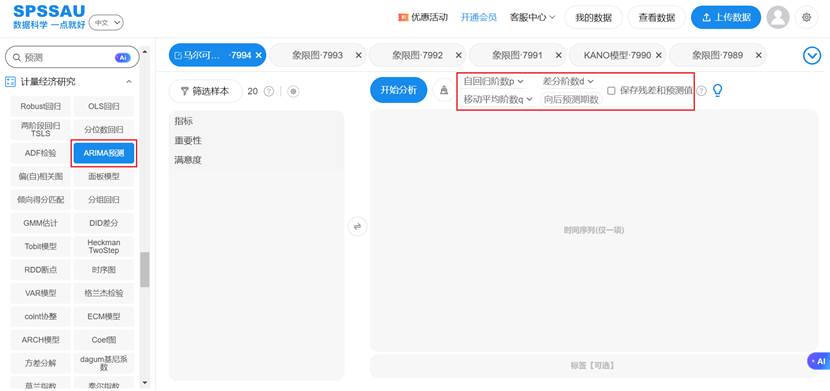
3. ARIMA 的适用场景

• 数据无明显季节性
• 数据呈现趋势，需要差分
• 数据复杂程度中等，线性结构可以解释大部分变化

三、季节性 ARIMA（SARIMA）：应对周期性最强的预测模型

现实中的时间序列大量存在强烈季节性：如电商销售额、温度、能源需求……若用普通 ARIMA，就等于忽略季节性 → 模型不准。因此出现了 SARIMA：ARIMA(p,d,q)(P,D,Q)s

其中：

• (p,d,q) = 普通部分
• (P,D,Q) = 季节部分
• s = 季节周期（如 12、4、7）

1. SARIMA 模型流程（Mermaid 图）

SARIMA 在 ARIMA 的基础上增加了季节维度，因此建模时不仅看 ACF/PACF，也要看季节滞后点（如 lag=12）的峰值。季节差分与普通差分交替进行，使序列在趋势与季节性两个维度均平稳。

2. SARIMA 的使用场景

• 数据具有明显周期性（如每月、每季度、每周）
• 季节性重复出现且稳定
• 预测时间跨度较长，需要考虑未来季节结构

SPSSAU 中 SARIMA 与 ARIMA 的建模流程一致，系统会自动识别季节周期，非常适合做年度或季度预测。

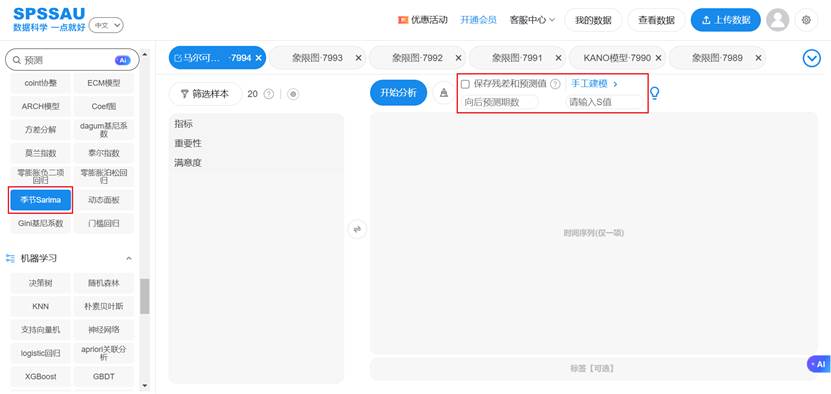
四、指数平滑法：结构简单但预测能力强

指数平滑法是一类非常经典的预测方法，其核心思想是：越新的数据对未来预测的影响越大，因此给予更高权重。

1. 三类指数平滑模型

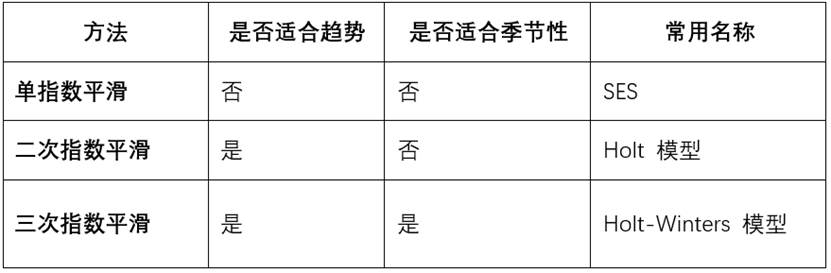
2. 指数平滑流程图（Mermaid）

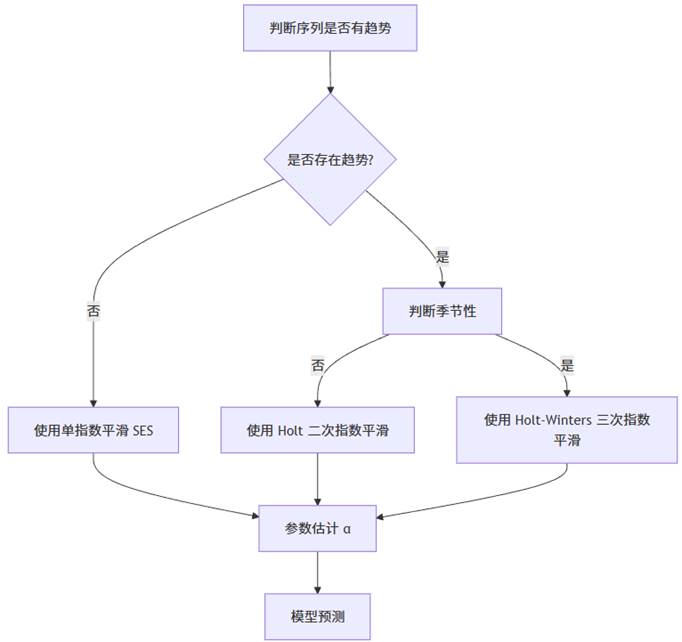
指数平滑完全依赖“成分分解”：水平方程、趋势方程、季节方程。
其优势在于运算简单、可解释性强、预测结果稳定，比 ARIMA 更便于理解。

3. 指数平滑的适用场景

• 适合趋势明显、季节性明显的数据
• 对异常值敏感度低
• 产品销售预测、气温预测、乘客流量预测等业务场景中极常用

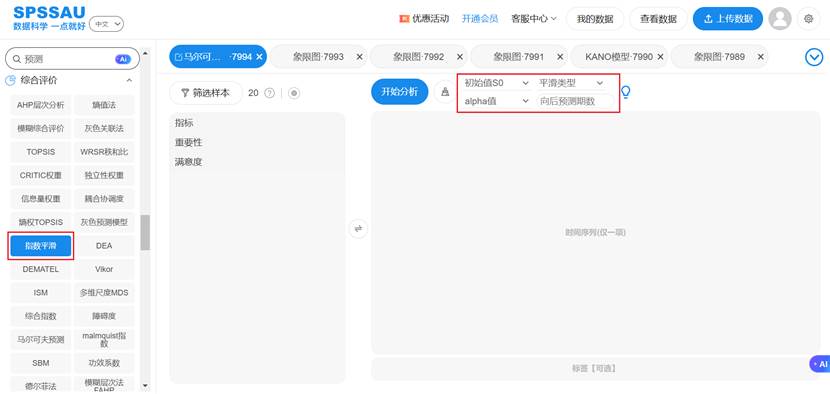
SPSSAU 的指数平滑模型如果不设置平滑方法，SPSSAU会自动遍历不同组合的平滑方法，找出最优效果时对应的平滑方法；如果不设置初始值S0，SPSSAU自动按照样本量情况设置初始值S0；如果不设置平滑系数alpha，SPSSAU自动遍历各种alpha取值情况，并且选择最优效果时对应的alpha值。

五、灰色预测模型：样本量极少时的“救命模型”

灰色预测是中国原创的预测方法论（灰色系统理论），特别适合“小样本、不确定性高”的情况。GM(1,1) 是最常见的灰色预测模型，其结构可以总结为：通过一次累加生成（AGO）让原始序列变得更“可建模”，再通过微分方程拟合增长率。

1. GM(1,1) 的建模机制

核心步骤：

1. 对序列进行一次累加 → 平滑序列
2. 建立一阶微分方程 x'(t) + a·x(t) = b
3. 求解模型参数 a、b
4. 得到预测序列
5. 逆累加还原结果（IAGO）

2. 灰色预测流程图（Mermaid）

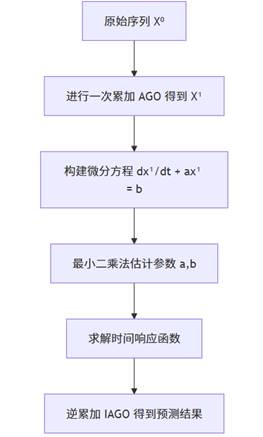
灰色模型的核心是“少数据预测”，只需要 4 个以上观测值即可建模，是在数据稀缺、系统不透明情况下的预测利器。

3. GM(1,1) 的适用场景

• 数据量极小（如 4～10 个观测值）
• 无法建立复杂统计模型
• 数据呈现指数增长或平滑变化趋势

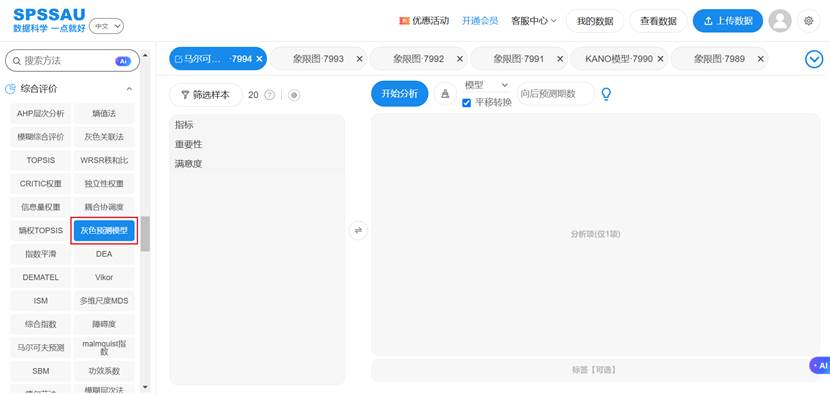
SPSSAU 中提供的 GM(1,1) 允许用户直接输入序列即可预测，特别适合指标数据缺失严重的情况下做趋势研判。

六、VAR 模型：处理多变量系统的“时序回归”

前面几个模型都属于单变量时间序列（Univariate）。
但现实世界常常不是一个指标单独变化，而是多个指标相互影响：例如：

• GDP ↔ 投资 ↔ 消费
• CPI ↔ PPI
• 利率 ↔ 汇率 ↔ 股票指数
• 企业流量 ↔ 销量 ↔ 投放预算

面对这种情况就需要：VAR（Vector AutoRegression）模型。

1. VAR 的基本思想

每个变量都由自己的滞后值 + 其他变量的滞后值解释。

2. VAR 模型流程 (Mermaid)

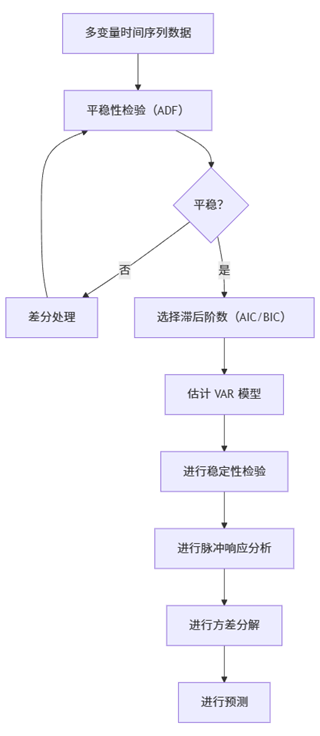
VAR 不只是预测，它还可以分析变量之间的动态影响（IRF）和贡献度（FEVD），是宏观经济政策分析最常用的工具之一。

3. VAR 的适用场景

• 多个变量相互影响
• 需要研究冲击效应与动态传导机制
• 需要变量之间的因果结构（配合 Granger 检验）

SPSSAU 的 VAR 模块集成 ADF、AIC/BIC、IRF、FEVD 等常见分析步骤，支持从“建模—解释—预测”一站式输出。

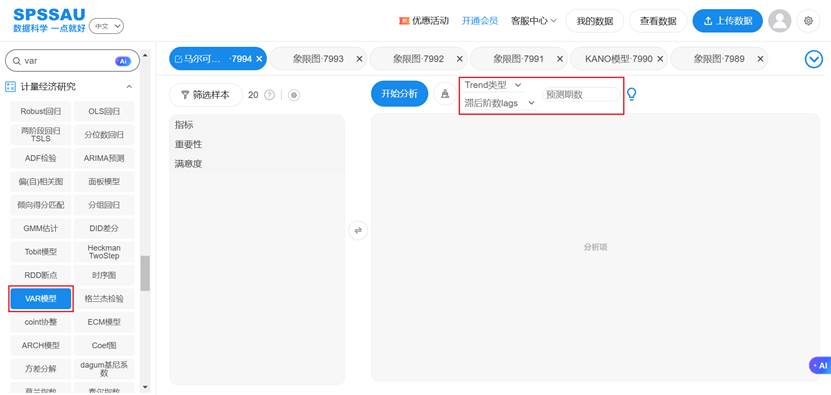
七、如何选择合适的时间序列预测方法？

用一张图总结最关键选择逻辑：

1. 按数据特征选择

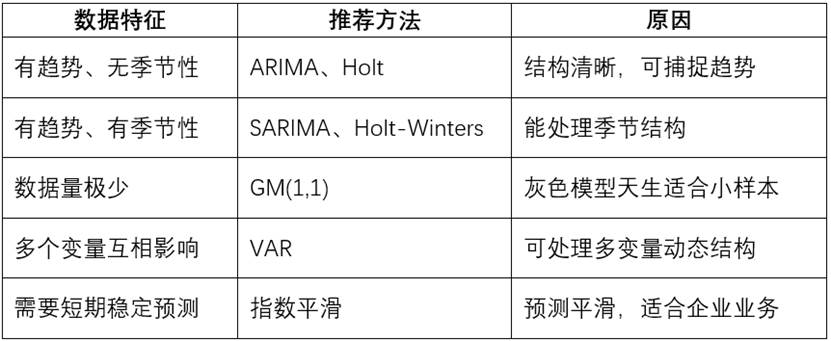
2. 按目的选择

• 预测未来：ARIMA/SARIMA、指数平滑
• 解释变量之间的影响：VAR
• 数据稀缺情况下的趋势研判：GM(1,1)

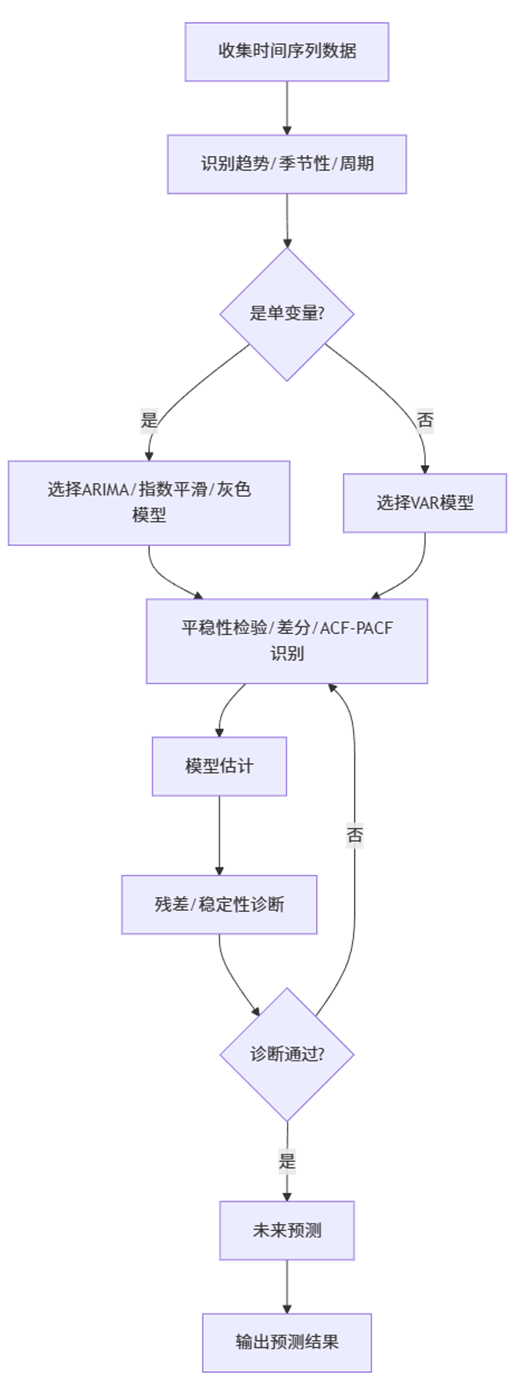
不论使用哪种模型，本质上都是——识别 → 建模 → 诊断 → 预测。SPSSAU 的好处在于，整个流程（尤其是识别、差分、模型诊断）均可自动完成，大幅降低了建模门槛。

九、总结：时间序列预测不是“选一个模型”这么简单

时间序列预测方法体系非常庞大，但可以用一句话总结：理解数据 → 理解模型 → 让模型适配数据

ARIMA/SARIMA 注重线性结构，指数平滑注重分解结构，灰色模型注重小样本预测，而 VAR 注重多变量的动态互动。

在实际研究中你会发现：

• 业务预测往往用指数平滑、SARIMA
• 经济金融研究多用 VAR、ARIMA
• 数据不足时灰色模型价值极高

如果你使用 SPSSAU，它能覆盖文中所有模型，可直接进行平稳性检验、差分、ACF/PACF 绘图、残差诊断、模型参数估计与未来预测，适合做论文、课题研究、业务预测等。