最好最差权重BWM原理与案例软件操作分析

1. 背景

BWM（Best-Worst Method，最好最差法）是一种多准则决策方法，由Jafar Rezaei于2015年提出。它通常用于确定决策标准的权重。与传统的AHP（层次分析法）相比，BWM简化了数据收集过程，只需确定“最优”和“最差”两个指标，并收集BO（Best-to-Other）和OW（Other-to-Worst）数据。

2. 理论

BWM的核心思想是通过数学规划求解，使得每个指标的权重与其实际重要性相匹配。具体步骤如下：

1. 确定准则指标：首先确定需要评估的准则或指标。
2. 确定最优和最差指标：从所有准则中选出最优和最差的指标。
3. 收集BO和OW数据：BO数据表示最优指标与其他各指标的相对重要性，OW数据表示其他各指标与最差指标的相对重要性。
4. 数学规划求解：通过数学规划方法求解各指标的权重，使得误差ε最小。

数学规划表达式如下：

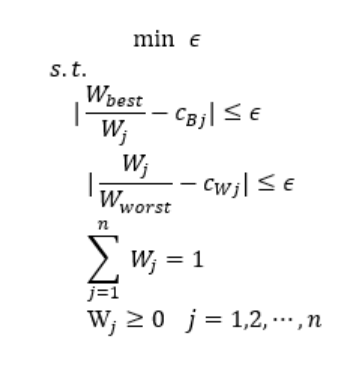
其中，W_best表示最优指标的权重，W_worst表示最差指标的权重，W_j表示某指标的权重，c_Bj表示第j个指标的BO数据，c_Wj表示第j个指标的OW数据，ε为误差。

3. 操作步骤

在SPSSAU(在线SPSS)中进行BWM权重计算的具体操作步骤如下：

1. 准备数据：准备好准则指标，并确定最优和最差指标。
2. 选择方法：在SPSSAU中选择“最好最差权重BWM”方法。
3. 输入数据：在SPSSAU中输入BO和OW数据。
4. 运行分析：点击“开始分析”按钮，SPSSAU将自动进行数学规划求解，并输出各指标的权重。
5. 结果解读：根据SPSSAU输出的权重结果，进行数据解读和应用。

4. SPSSAU输出结果

SPSSAU将输出以下结果：

• BWM权重结果：各指标的权重值。
• 一致性指数（CI）：用于评估数据的一致性，CI值越小，一致性越好。

5. 案例实操

假设我们有一份数据，包含5个指标，其BO和OW数据如下：

在SPSSAU中输入上述数据，并运行BWM分析，得到各指标的权重如下：

6. 文字分析

从结果可以看出，指标2的权重最高（45.40%），说明在决策中指标2的重要性最高。而指标5的权重最低（5.54%），说明其重要性最低。通过BWM方法，我们可以清晰地了解各指标在决策中的相对重要性，从而做出更合理的决策。

7. 疑难解惑

• 如何确定最优和最差指标？：最优和最差指标通常由专家或决策者根据实际情况确定。
• BO和OW数据如何收集？：BO和OW数据通常通过专家打分或问卷调查的方式收集。
• 一致性指数（CI）的意义是什么？：CI值用于评估数据的一致性，CI值越小，说明数据的一致性越好，结果越可靠。

通过SPSSAU(网页SPSS)的BWM方法，我们可以高效、准确地完成多准则决策分析，为决策提供科学依据。