在本文开始之前,我们先了解一下算子的概念。
算子英语是 Operator,它是一个函数空间到函数空间上的映射 O:X→X。广义上的算子可以推广到任何空间。
函数是从数到数的映射。
泛函是从函数到数的映射。
算子是从函数到函数的映射。
算子不等同于函数,也不等同于算法。算法是更为广泛的概念,它包含了算子。
Part11. Roberts 算子
我们知道用 L1 范数来近似梯度的幅度:
其中,
在 x 方向,由偏导公式可知,其实就是相邻两个像素的值相减。同理,y 方向也是如此。因此可以得到如下算子。

类似地,还有对角线方向。对于对角线方向梯度,公式和算子如下:
Roberts 卷积核:

我们可以实现一个基于 roberts 算子的边缘检测
#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
using namespace std;
using namespace cv;
void roberts(Mat& input, Mat& output, Mat& kernel_x, Mat& kernel_y)
{
int height = input.rows;
int width = input.cols;
int height_x = kernel_x.rows;
int width_x = kernel_x.cols;
int height_y = kernel_y.rows;
int width_y = kernel_y.cols;
for (int row = 1; row < height - 1; row++)
{
for (int col = 1; col < width - 1; col++)
{
float G_X = 0;
for (int h = 0; h < height_x; h++)
{
for (int w = 0; w < width_x; w++)
{
G_X += input.at<uchar>(row + h, col + w) * kernel_x.at<float>(h, w);
}
}
float G_Y = 0;
for (int h = 0; h < height_y; h++)
{
for (int w = 0; w < width_y; w++)
{
G_Y += input.at<uchar>(row + h, col + w) * kernel_y.at<float>(h, w);
}
}
output.at<uchar>(row, col) = saturate_cast<uchar>(cv::abs(G_X) + cv::abs(G_Y));
}
}
}
int main(int argc,char *argv[])
{
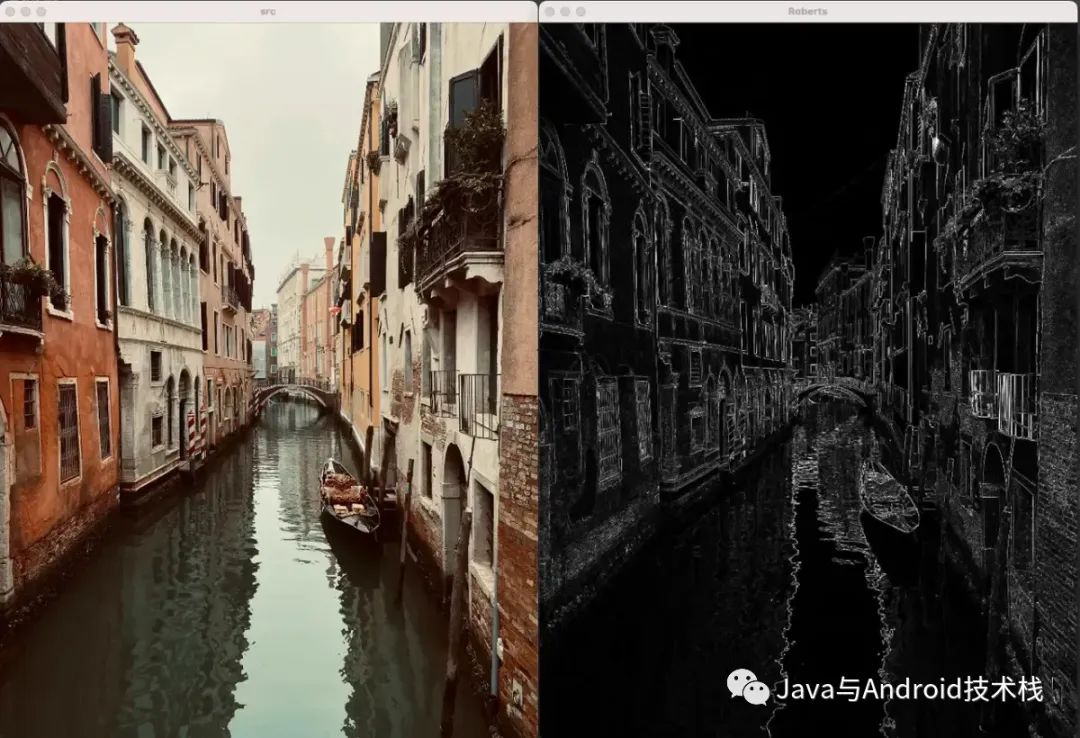
Mat src = imread(".../street.jpg");
imshow("src",src);
Mat gray;
cv::cvtColor(src, gray, COLOR_BGR2GRAY);
Mat kernelRoX = (cv::Mat_<float>(2,2) << -1,0,0,1);
Mat kernelRoY = (cv::Mat_<float>(2,2) << 0,-1,1,0);
Mat dst;
dst.create(gray.rows,gray.cols,gray.type());
roberts(gray, dst, kernelRoX, kernelRoY);
imshow("Roberts",dst);
waitKey(0);
return 0;
}
也可以用 OpenCV 自定义的滤波器 filter2D() 函数,来实现 Roberts 边缘检测:
int main(int argc,char *argv[])
{
Mat src = imread(".../street.jpg");
imshow("src",src);
Mat gray;
cv::cvtColor(src, gray, COLOR_BGR2GRAY);
Mat kernelRoX = (cv::Mat_<float>(2,2) << -1,0,0,1);
Mat kernelRoY = (cv::Mat_<float>(2,2) << 0,-1,1,0);
Mat dstRoX;
Mat dstRoY;
cv::filter2D(gray,dstRoX,-1,kernelRoX);
cv::filter2D(gray,dstRoY,-1,kernelRoY);
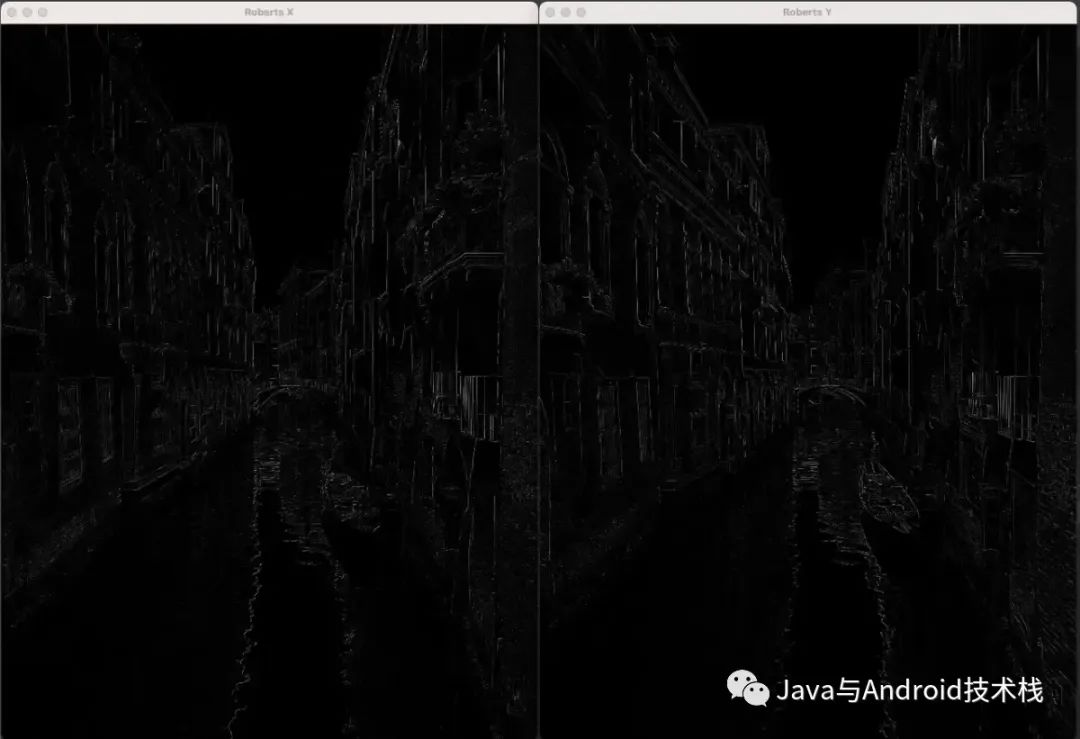
imshow("Roberts X", dstRoX);
imshow("Roberts Y", dstRoY);
dstRoX = cv::abs(dstRoX);
dstRoY = cv::abs(dstRoY);
Mat dst;
add(dstRoX,dstRoY,dst);
imshow("Roberts", dst);
waitKey(0);
return 0;
}

Part22. Prewitt 算子
在下图的 3×3 区域,Roberts 算子利用和,实现对角差分。
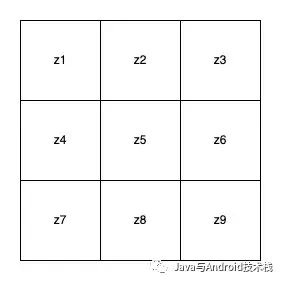
但是 2×2 大小的核概念上很简单,但在计算边缘方向时,它们不如中心对称的核有用,中心对称核的最小尺寸为 3×3。
Prewitt 算子的设计思想:真正的边界点在水平方向和垂直方向上的相邻点应该也同样为边界点,因此以更大的边缘检测滤波器,考虑周围更多的点会使得边缘检测更准确。
Prewitt 卷积核:
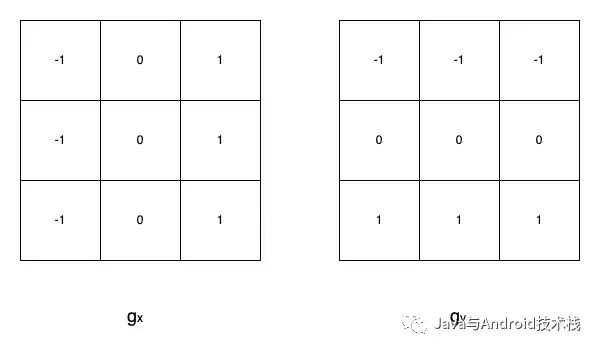
Prewitt 算子如下:
#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
using namespace std;
using namespace cv;
void prewitt(Mat& input, Mat& output, Mat& kernel_x, Mat& kernel_y)
{
int height = input.rows;
int width = input.cols;
int height_x = kernel_x.rows;
int width_x = kernel_x.cols;
int height_y = kernel_y.rows;
int width_y = kernel_y.cols;
for (int row = 1; row < height - 1; row++)
{
for (int col = 1; col < width - 1; col++)
{
float G_X = 0;
for (int h = 0; h < height_x; h++)
{
for (int w = 0; w < width_x; w++)
{
G_X += input.at<uchar>(row + h - 1, col + w - 1) * kernel_x.at<float>(h, w);
}
}
float G_Y = 0;
for (int h = 0; h < height_y; h++)
{
for (int w = 0; w < width_y; w++)
{
G_Y += input.at<uchar>(row + h - 1, col + w - 1) * kernel_y.at<float>(h, w);
}
}
output.at<uchar>(row, col) = saturate_cast<uchar>(cv::abs(G_X) + cv::abs(G_Y));
}
}
}
int main(int argc,char *argv[])
{
Mat src = imread(".../street.jpg");
imshow("src",src);
Mat gray;
cv::cvtColor(src, gray, COLOR_BGR2GRAY);
Mat kernelPrewittX = (cv::Mat_<float>(3,3) << -1,0,1,-1,0,1,-1,0,1);
Mat kernelPrewittY = (cv::Mat_<float>(3,3) << -1,-1,-1,0,0,0,1,1,1);
Mat dst;
dst.create(gray.rows,gray.cols,gray.type());
prewitt(gray, dst, kernelPrewittX, kernelPrewittY);
imshow("Prewitt", dst);
waitKey(0);
return 0;
}
用 OpenCV 自定义的滤波器 filter2D() 函数,来实现 Prewitt 边缘检测:
int main(int argc,char *argv[])
{
Mat src = imread(".../street.jpg");
imshow("src",src);
Mat gray;
cv::cvtColor(src, gray, COLOR_BGR2GRAY);
Mat kernelPrewittX = (cv::Mat_<float>(3,3) << -1,0,1,-1,0,1,-1,0,1);
Mat kernelPrewittY = (cv::Mat_<float>(3,3) << -1,-1,-1,0,0,0,1,1,1);
Mat dstPrewittX;
Mat dstPrewittY;
cv::filter2D(gray,dstPrewittX,-1,kernelPrewittX);
cv::filter2D(gray,dstPrewittY,-1,kernelPrewittY);
imshow("Prewitt X", dstPrewittX);
imshow("Prewitt Y", dstPrewittY);
dstPrewittX = cv::abs(dstPrewittX);
dstPrewittY = cv::abs(dstPrewittY);
Mat dst;
add(dstPrewittX,dstPrewittY,dst);
imshow("Prewitt", dst);
waitKey(0);
return 0;
}Prewitt X 检测垂直的边界,Prewitt Y 检测水平的边界。

下图展示的是联合梯度。

Part33. Sobel 算子
Roberts 算子按照对角线两个方向的梯度确定边缘点,Prewitt 算子按照水平和垂直方向的梯度确定边缘点。
上面我们通过使用 cv::filter2D() 函数来实现这2种边缘检测,都展示了其对两个方向对边缘的检测的效果图,我们发现不同方向梯度的边缘检测效果各有特点。
融合多种方向的梯度,能够有效提升边缘检测效果。Sobel 算子考虑了水平、垂直和两个对角,共计4个方向对的梯度加权求和。
Sobel 的作者定义了一个给定邻域方向的梯度矢量 g 的幅度为:
像素灰度差分像素距离
其中,像素距离使用曼哈顿距离进行计算。
之前在第六篇介绍过曼哈顿距离,表示从像素 p 向像素 q 出发,每次能走的点必须是在当前像素点的 4 邻域中。一步一步走到 q 点后,一共经过的像素点数就是曼哈顿距离。
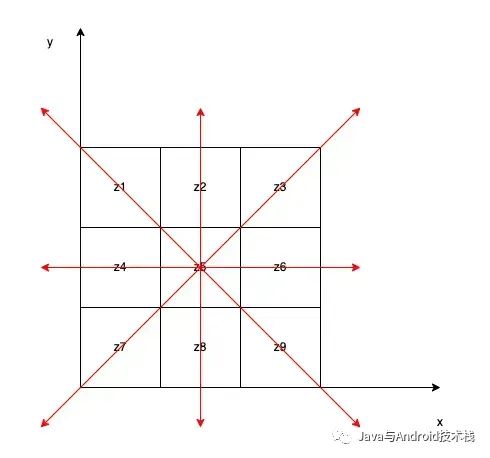
矢量 g 的方向可以通过中心像素 z5 相关邻域的单位矢量给出,这里的邻域是对称出现的,即四个方向对:(z1,z9),(z2,z8),(z3,z7),(z6,z4)。沿着4个方向对上求其梯度矢量和,可以得到像素 z5 的平均梯度估计。
公式中 4个单位向量 [1, 1],[-1, 1],[0, 1], [1, 0] 控制差分的方向,系数 1/4, 1/2 为距离反比权重。例如 z1 到 z9 的曼哈顿距离是 4,z2 到 z8 的曼哈顿距离是 2。
对于上述公式,为了避免具有小数的乘除计算,因此对 G 乘上缩放因子 4
可得,Sobel 算子如下:
Sobel 卷积核:

#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
using namespace std;
using namespace cv;
void sobel(Mat& input, Mat& output, Mat& kernel_x, Mat& kernel_y)
{
int height = input.rows;
int width = input.cols;
int height_x = kernel_x.rows;
int width_x = kernel_x.cols;
int height_y = kernel_y.rows;
int width_y = kernel_y.cols;
for (int row = 1; row < height - 1; row++)
{
for (int col = 1; col < width - 1; col++)
{
float G_X = 0;
for (int h = 0; h < height_x; h++)
{
for (int w = 0; w < width_x; w++)
{
G_X += input.at<uchar>(row + h - 1, col + w - 1) * kernel_x.at<float>(h, w);
}
}
float G_Y = 0;
for (int h = 0; h < height_y; h++)
{
for (int w = 0; w < width_y; w++)
{
G_Y += input.at<uchar>(row + h - 1, col + w - 1) * kernel_y.at<float>(h, w);
}
}
output.at<uchar>(row, col) = saturate_cast<uchar>(cv::abs(G_X) + cv::abs(G_Y));
}
}
}
int main(int argc,char *argv[])
{
Mat src = imread(".../street.jpg");
imshow("src",src);
Mat gray;
cv::cvtColor(src, gray, COLOR_BGR2GRAY);
Mat kernelSobelX = (cv::Mat_<float>(3,3) << -1,0,1,-2,0,2,-1,0,1);
Mat kernelSobelY = (cv::Mat_<float>(3,3) << -1,-2,-1,0,0,0,1,2,1);
Mat dst;
dst.create(gray.rows,gray.cols,gray.type());
sobel(gray, dst, kernelSobelX, kernelSobelY);
imshow("Sobel", dst);
waitKey(0);
return 0;
}
用 OpenCV 自带的 Sobel() 函数来实现其边缘检测
int main(int argc,char *argv[])
{
Mat src = imread(".../street.jpg");
imshow("src",src);
Mat gray;
cv::cvtColor(src, gray, COLOR_BGR2GRAY);
Mat dstSobelX;
Mat dstSobelY;
Sobel(gray, dstSobelX, CV_16S, 1, 0, 3);
Sobel(gray, dstSobelY, CV_16S, 0, 1, 3);
convertScaleAbs(dstSobelX, dstSobelX);
convertScaleAbs(dstSobelY, dstSobelY);
imshow("Sobel X", dstSobelX);
imshow("Sobel Y", dstSobelY);
Mat dst;
add(dstSobelX,dstSobelX,dst);
imshow("Sobel", dst);
waitKey(0);
return 0;
}

OpenCV 提供的Sobel() 函数,稍微解释一下几个参数的含义
void Sobel( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, int ksize = 3,
double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );第三个参数 ddepth:表示输出梯度的数据类型
若 src.depth() = CV_8U,则 ddepth =-1/CV_16S/CV_32F/CV_64F
若 src.depth() = CV_16U/CV_16S,则 ddepth =-1/CV_32F/CV_64F
若 src.depth() = CV_32F,则 ddepth =-1/CV_32F/CV_64F
若 src.depth() = CV_64F,则 ddepth = -1/CV_64F
第四个参数 dx:导数在 x 轴方向的阶数。dx=1, dy=0 表示对 x 方向计算梯度。
第五个参数 dy:导数在 y 轴方向的阶数。dx=0, dy=1 表示对 y 方向计算梯度。
第六个参数 ksize:Sobel 卷积核的大小,使用 3、5、7、9、11 等等。
Part44. 总结
在实际的图像分割中,我们往往只用一阶、二阶导数,他们都各有优势。 Roberts、Prewitt、Sobel 算子是一阶导数的边缘算子,通过卷积核与图像的每个像素点做卷积和运算,然后选取合适的阈值来提取图像的边缘。本文分别用这些算子对同一幅图像进行边缘检测,可以看到不同的效果,等到介绍完所有常用的算子后会对他们做一个总结。
另外,我们之前介绍过 Laplace 算子,它是二阶导数算子,后面的文章还会继续介绍二阶导数的边缘算子。
【Java与Android技术栈】公众号
关注 Java/Kotlin 服务端、桌面端 、Android 、机器学习、端侧智能
更多精彩内容请关注:




 本文详细介绍了OpenCV中的Roberts、Prewitt和Sobel边缘检测算子。Roberts算子通过L1范数近似梯度,Prewitt算子采用中心对称核提高边缘检测准确性,而Sobel算子综合多个方向的梯度。文章通过实例展示了如何使用OpenCV实现这些算子,并比较了它们在图像边缘检测中的效果。
本文详细介绍了OpenCV中的Roberts、Prewitt和Sobel边缘检测算子。Roberts算子通过L1范数近似梯度,Prewitt算子采用中心对称核提高边缘检测准确性,而Sobel算子综合多个方向的梯度。文章通过实例展示了如何使用OpenCV实现这些算子,并比较了它们在图像边缘检测中的效果。
















 2067
2067

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








