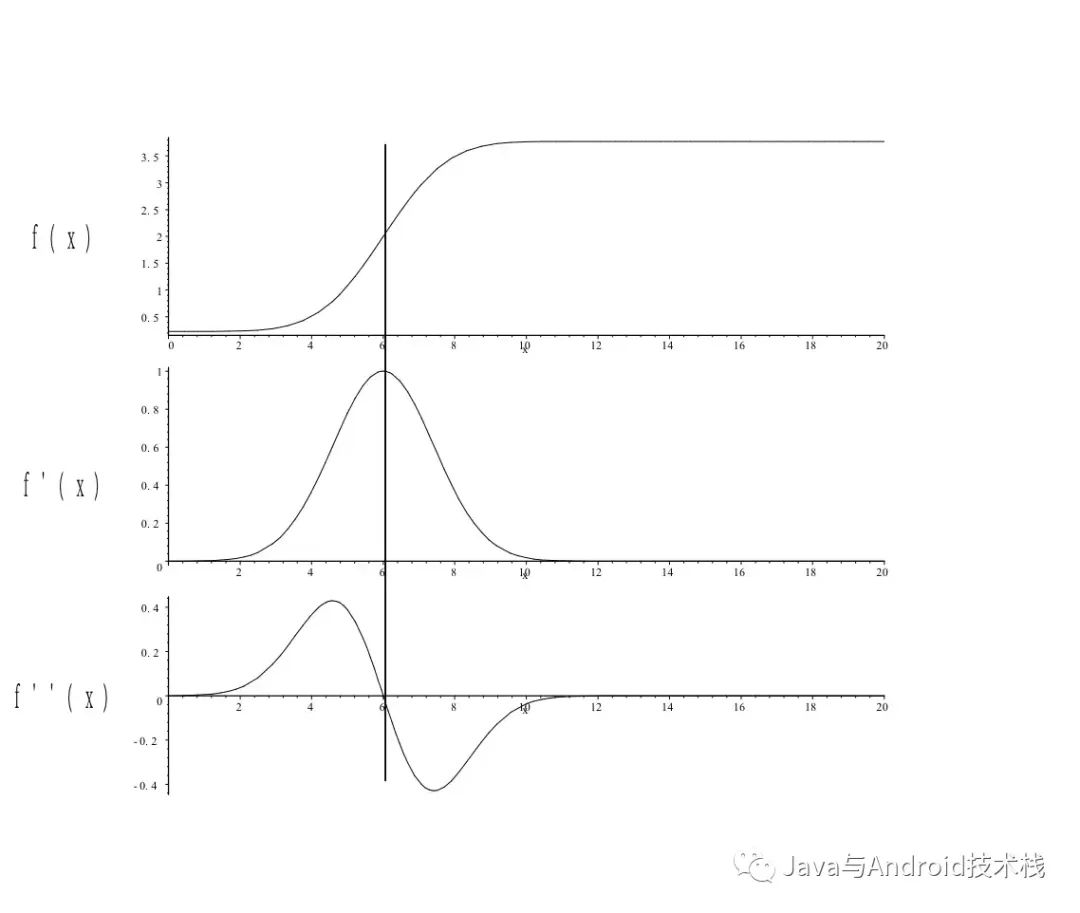
在该系列的第八篇文章中,我们曾介绍过一阶导数和二阶导数对分析边缘的结论:
一阶导数通常在图像中产生较粗的边缘;
二阶导数对精细细节,如细线、孤立点和噪声有较强的响应;
二阶导数在灰度斜坡和灰度台阶过渡处会产生双边缘响应;
二阶导数的符号可用于确定边缘的过渡是从亮到暗还是从暗到亮。
一阶导数算子(例如 Sobel 算子)通过对图像求导来确定图像的边缘,数值绝对值较高的点对应了图像的边缘。如果继续求二阶导,原先数值绝对值较高的点对应了过零点。因此,也可以通过找到二阶导数的过零点来检测边缘。在某些情况下,找二阶导数的过零点可能更容易。
Part11. Laplace 算子
之前我们曾介绍过二阶导数的 Laplace 算子可以通过差分近似来简化,其公式为
它的卷积核:
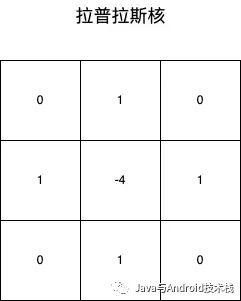
这是它的 4 邻域卷积核。
11.1 Laplace 算子的扩展
Laplace 算子是具有旋转不变性的各向同性的算子。
将 4 邻域的 Laplace 算子旋转 45° 后,与原算子相加,就可以得到 8 邻域的算子。
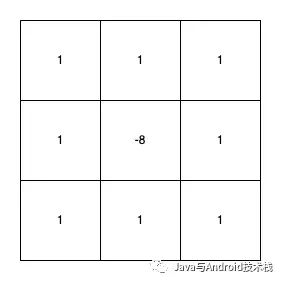
这是它的 8 邻域卷积核。这个算子表示一个像素周围一圈 8 个像素的和与中间像素 8 倍的差,作为拉普拉斯计算结果。
另外,还有两个拉普拉斯卷积核,分别是对 4 邻域卷积核和 8 邻域卷积核取反。





 本文介绍了OpenCV中的Laplace和LoG算子,作为二阶导数边缘检测工具。Laplace算子通过4邻域和8邻域卷积核检测边缘,但对噪声敏感。LoG算子结合高斯平滑与Laplace算子,提供更好的抗噪声能力,常用于边缘定位。
本文介绍了OpenCV中的Laplace和LoG算子,作为二阶导数边缘检测工具。Laplace算子通过4邻域和8邻域卷积核检测边缘,但对噪声敏感。LoG算子结合高斯平滑与Laplace算子,提供更好的抗噪声能力,常用于边缘定位。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 9535
9535

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








