11.自编码器及变分自编码器

最新推荐文章于 2025-05-05 21:01:36 发布

不要瞎胡闹

最新推荐文章于 2025-05-05 21:01:36 发布

阅读量867

点赞数 1

CC 4.0 BY-SA版权

分类专栏：深度学习&Tensorflow 文章标签：人工智能自编码器 tensorflow 深度学习神经网络

本文链接：https://blog.youkuaiyun.com/SDFJXVC/article/details/103975239

深度学习&Tensorflow 专栏收录该内容

18 篇文章

订阅专栏

代码点这里

1.自编码器(Autoencoder)

自编码器的介绍可以点击这里。
自编码器包含两部分：编码器与解码器。
编码器相当于把数据压缩，解码器相当于将数据解压。
编码就是数据降维，解码就是升维，之前的神经网络与卷积网络都叙述过，不再赘诉。
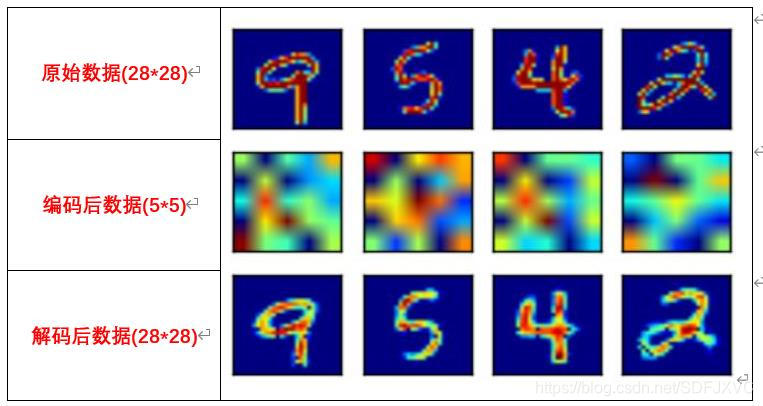
在这里插入图片描述

2.去噪自编码(Denoising AE)

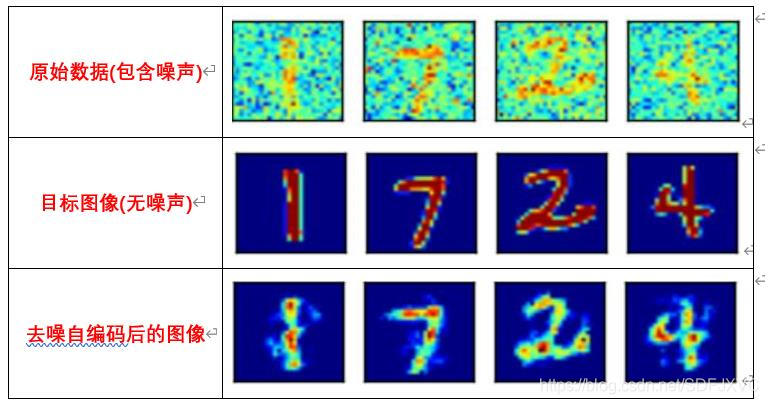
去噪自编码与自编码器类似，都是编码与解码的过程。
只是去噪自编码中原始数据是具有噪声的，通过去噪自编码器后，可以将数据中的噪声去除。
在这里插入图片描述

3.变分自编码器(VAE)

3.1VAE是什么

自编码是将图片编码再解码还原，而VAE的作用是求出编码后的P(Z|X)的分布，这样我们就可以用P(Z|X)来生成我们想要的数据。
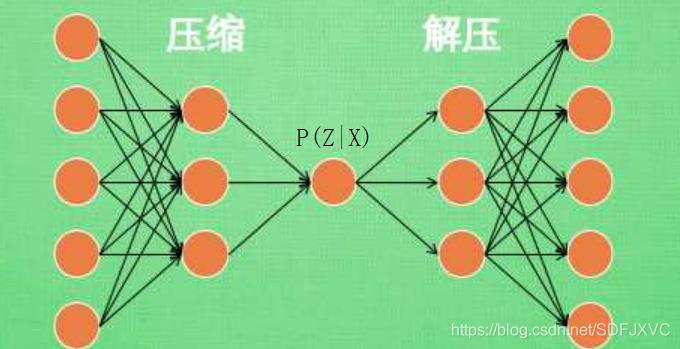
在这里插入图片描述
简单来说，之前自编码是：
$(X_1,X_2,X_3,....X_n)\to(Z_1,Z_2,Z_3,...Z_n)$
而VAE则是：
$(X_1,X_2,X_3,....X_n)\to P(Z|X)$
这样我们就不需要每次存储 $Z_1,Z_2,Z_3,...Z_n)$ 了，只需要知道他们的分布就可以了！
举个栗子：
(1) $(X_1,X_2,X_3,....X_n)\to(1,2,3,...n)$
(2) $(X_1,X_2,X_3,....X_n)\to(P(Z|X) = i),0< i\leq n$
明显(2)比(1)的方式要好！

3.2相关公式：

(1)朴素贝叶斯：
$P(A\cap B) = P(B|A)*P(A)=P(A|B)*P(B)$
(2)KL散度 :
$KL(P||Q)=\sum P(x)*log\frac{P(x)}{Q(x)}$
(3)正态分布：
$N(\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$
(4) $KL\Big(N(\mu,\sigma^2)||N(0,1)\Big)：$
在这里插入图片描述
推导过程摘自变分自编码器（一）：原来是这么一回事

3.3推导过程

(1) $P(Z|X)=\frac{P(X|Z)*P(Z)}{P(X)}$

(2) 假设存在一个 $Q = Q (Z ∣ X)$ 与 $P = P (Z ∣ X)$ 近似，则他们的KL散度是：

$\begin{aligned} KL\big(Q||P\big) &=\sum Q*log\frac{Q}{P}\\ & =\sum Q*log\frac{Q*P(X)}{P(X|Z)*P(Z)}\\ &= \sum Q*log\frac{Q}{P(X|Z)}+\int (Q*logP(X)-Q*logP(Z))dz\\ &=KL(Q||P(Z)) - \int Q*logP(X|Z)dz+logP(X)\\ \end{aligned}$
其中 $\int Q*logP(X)dz =logP(X)$ ，是个常数。
$要使Q与P近似\to KL(Q||P)要尽量小$
$\to KL(Q||P(Z))-\int Q*logP(X|Z)dz尽量小。$

(3)假设：

$=N(\mu,\sigma^2)$
$② P (Z)$ 是一个单位多元正态分布 $N (0, I)$ 。
关于多元正态分布点击多元高斯分布。
结合上面相关公式(4)，得出以下结果：
$KL\big(N(\mu,\sigma^2)||P(Z)\big) = \frac{1}{2}*\sum_i(-log\sigma_i^2-1+\mu^2+\sigma_i^2)$

#KL散度
#logvar是方差的对数
KLD = 0.5*tf.reduce_sum(tf.pow(mu, 2) + tf.exp(logvar) - 1 - logvar,1)

(4)重参数化技巧(Reparameterization Trick)

从上面的过程，我们知道了要训练 $KL\big(Q||P\big)$ ，就需要计算 $=N(\mu,\sigma^2)$ ，见下图：

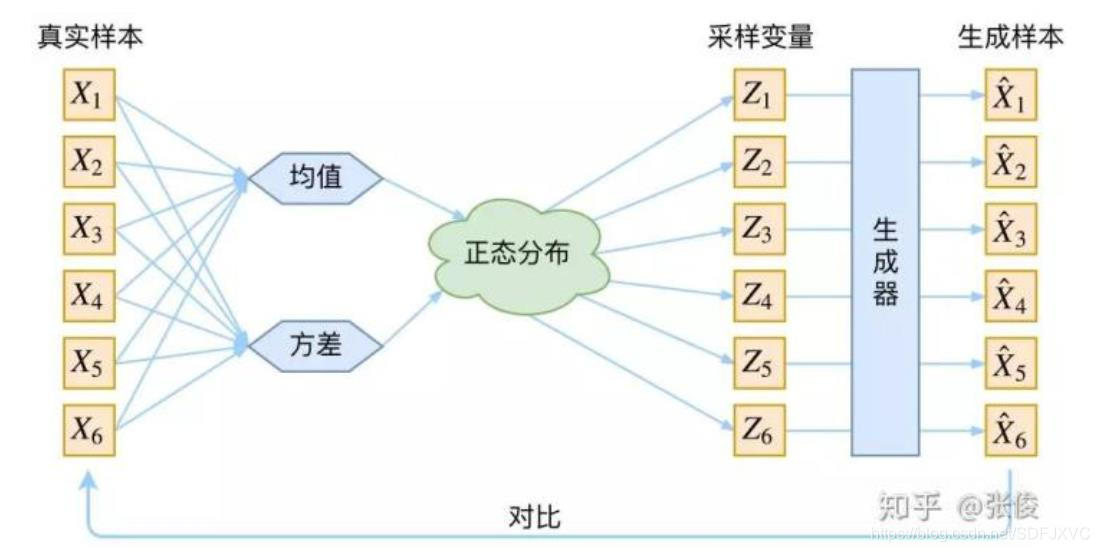
图片转载自变分自编码器VAE：原来是这么一回事。
但是 $\mu与\sigma$ 是无法进行梯度计算的，所以我们就用到重参数化技巧：
如果非标准正态分布 $X\sim N(μ,σ^2)$ ，那么关于 $X$ 的一个一次函数 $Y = (X - μ) / σ$ ，就一定是服从标准正态分布 $N (0, 1) 。$ 证明详见：普通正态分布如何转换到标准正态分布。
所以我们可以将 $P(Z|X)\sim N(\mu,\sigma^2)$ 写成
$P(Z|X)\sim \mu+N(0,1)*\sigma$

def sample_z(mu,log_var):
    #标准正态分布
    eps = tf.random_normal(shape=tf.shape(mu))
    #返回Z的分布，log_var是方差的对数
    return mu + tf.exp(log_var / 2) * eps

(5)解码

通过将图片编码后得到了 $P(Z|X)\sim \mu+N(0,1)*\sigma$ ，这样我们就可以通过解码得到 $P (X ∣ Z)$ ，即将图像进行了还原，所以需要重构损失，计算还原后的图像与原图像的损失：

#重构损失,比较还原的图像与原图像的损失
BCE = tf.reduce_sum(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=X),1)

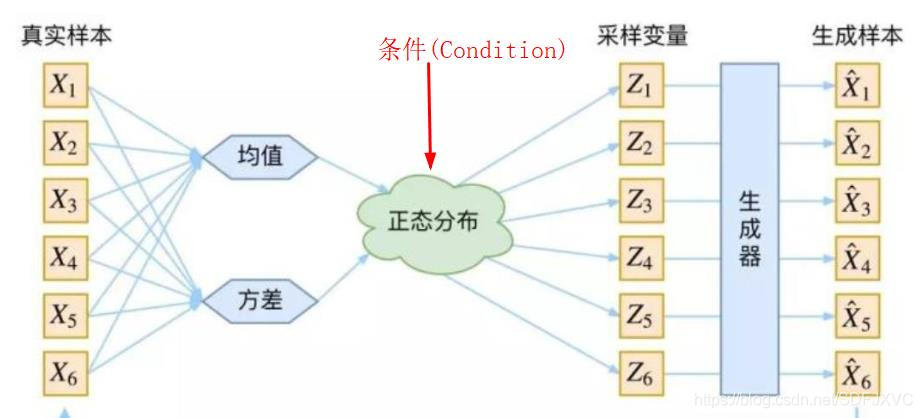
4.条件变分自编码器(CVAE)

CVAE只是在VAE的基础上将图像的标签添加到网络中，结构如图：
在这里插入图片描述

#计算Z
def sample_z(mu,log_var):
    #标准正态分布
    eps = tf.random_normal(shape=tf.shape(mu))
    #Z的分布
    return mu + tf.exp(log_var / 2) * eps

#获取Z的分布
z = sample_z(mu,logvar)
#将标签加入Z中
z_c = tf.concat([z,Y],1)