本文依旧来源于研读下面这篇文章:
零基础入门深度学习(4) - 卷积神经网络_0基础学卷积神经网络-优快云博客
放个传送门在这:小白学习machine learning的第一天-优快云博客
小白学习machine learning的第二天-优快云博客
小白学习machine learning的第三天-优快云博客
小白学习machine learning的第四天-优快云博客
小白学习machine learning的第五天-优快云博客
小白学习machine learning的第六天-优快云博客
今天是万众瞩目的卷积神经网络呀!
一、介绍一下卷积神经网络
(1)首先,因为卷积神经网络更加适合图像、语音识别。
①参数数量过多:就是一个像素点要一个隐藏层节点,数量太夸张了啊啊啊
②像素点的远近相邻关系会被忽略,因为每个节点单独计算,这不是图像识别所需要的呀
③全连接神经网络难以深度到3层以后,而神经网络一般越多层提取的特征越多,表达能力也就越强
(2)那么,我们来看看卷积神经网络吧!
- 局部连接
每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连,减少了很多参数。 - 权值共享
一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。 - 下采样
可以使用Pooling(池化,就是浓缩特征呀,有平均池化和最大池化)来减少每层的样本数,进一步减少参数数量,同时还可以提升模型的鲁棒性(强调系统在不利条件下的稳定性和可靠性,作者也不知道是搜的哈哈)。
(3)其次,这里我们使用relu函数作为替代sigmoid函数为激活函数:
①速度快,只用max(0,x)就可以完成代码。
②减轻梯度消失问题,![]() ,而sigmoid的导数每次都会变小,所以这里用relu不会变。
,而sigmoid的导数每次都会变小,所以这里用relu不会变。
③稀疏性,sigmoid激活率为50%远大于人脑3%,而relu再15%-30%的最佳区间。(这……)
(4)看图呀
说句题外话:这里作者建议学卷积搭配yolo的博客一起食用更佳哦。
放个传送门:YOLO系列算法精讲:从yolov1至yolov8的进阶之路(2万字超全整理)-优快云博客
咋们继续!
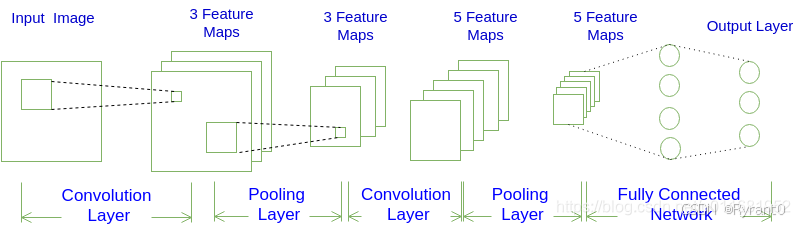
不难发现,卷积神经网络的结构为:
INPUT -> [[CONV]*N -> POOL]*M -> [FC]*K
也就是N个卷积层叠加,然后(可选)叠加一个Pooling层,重复这个结构M次,最后叠加K个全连接层。
我们瞅瞅具体怎么做的:
①输入层,输入层的宽度和高度对应于输入图像的宽度和高度,而它的深度为1。
②进行卷积操作(作者后面会讲滴)得到第一个卷积层,得到(filter(超参数)取3)个feature map/channel。其实就是提取了3组原始图像的不同特征。
③对3个feature map都进行了pooling下采样得到更精致的3个feature map,把它们融进第二个有5个filter的卷积层中,得到新的5个filter。再对这5个filter进行pooling下采样得到5个更小的feature map
④我们最后再通过2个全连接层,第一个与5个feature map中所有神经元相连,然后第二个与第一个全连接,最后得到结果输出呀!O(∩_∩)O
(5)来看看对于每个图像具体计算方式:
①
绿色为原始图像,黄色为过滤层,红色为特征图。
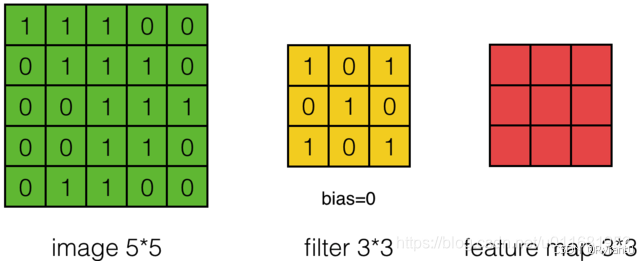
如下图可以计算出原始图像 * 过滤层权重 = feature map各个点的数值。
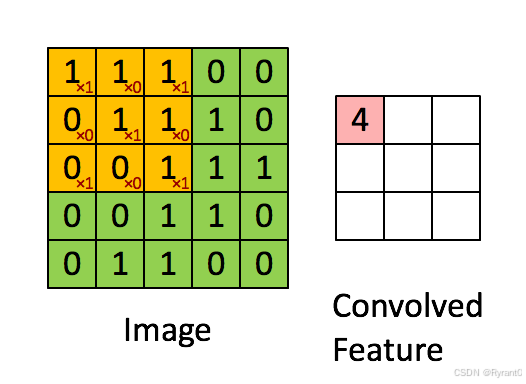
这是公式了呀,但我觉得直观还是图形会好理解一点。
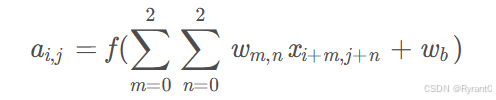
那么,哪怕是换了feature map的大小,也就是变化了步长而已呀。
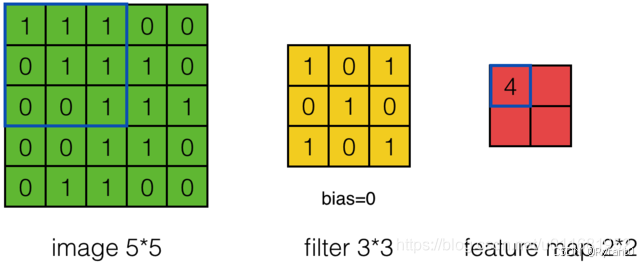
接下来,我们来看看公式,其实直观感受也很干脆能判断出来步长,除非数值较大那就得用公式了呢。
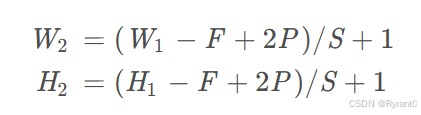
W2是卷积后Feature Map的宽度;W1是卷积前图像的宽度;F是filter的宽度;P是Zero Padding数量,Zero Padding是指在原始图像周围补几圈0,如果的值是1,那么就补1圈0;S是步长;H2是卷积后Feature Map的高度;H1是卷积前图像的宽度。(式2和式3本质上是一样的)
②那么,如果深度 > 1又该怎么办呢?
我们变形一下公式:
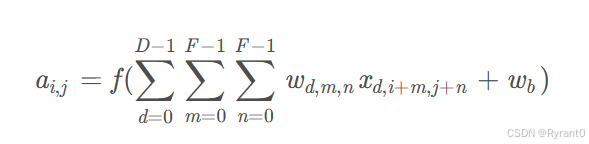
D是深度;F是filter的大小(宽度或高度,两者相同);wd,m,n表示filter的第d层第m行第n列权重;ad,i,j表示图像的第d层第i行第j列像素。
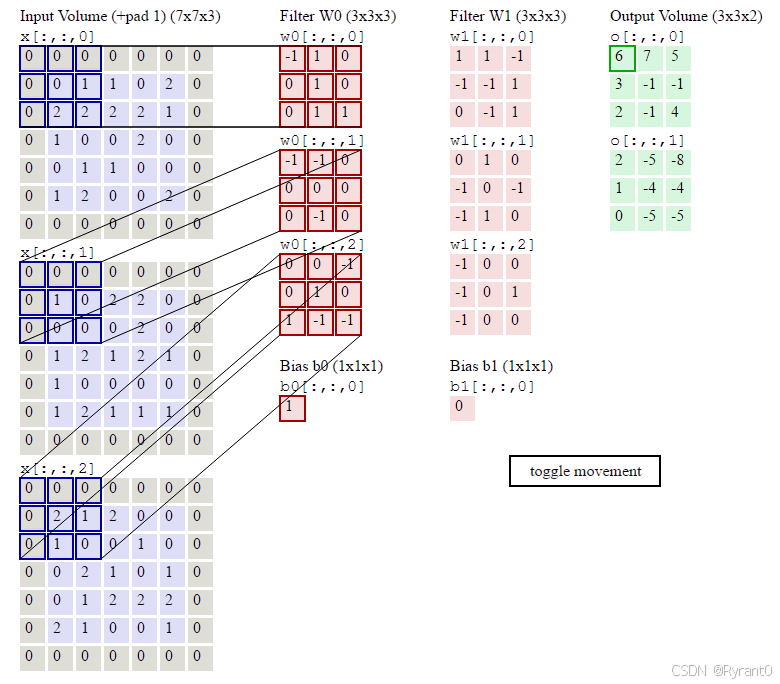
如上图所示,sero padding的加入很好的防止了边缘数据取到的次数少于中心数据的问题,利于图像边缘部分的特征提取。
那么,以上就是卷积层的计算方法啦。这里面体现了局部连接和权值共享:每层神经元只和上一层部分神经元相连(卷积计算规则),且filter的权值对于上一层所有神经元都是一样的。对于包含两个333的fitler的卷积层来说,其参数数量仅有(3*3*3+1)*2=56个,且参数数量与上一层神经元个数无关。与全连接神经网络相比,其参数数量大大减少了。
(6)用卷积神经网络公式来表示卷积层计算
全是数学公式计算,详见原文哦!
(7)pooling层的计算
①max pooling:就是取一个feature map的一定区域内的最大权值/比重的数据作为“浓缩”
后的数据。
②Mean pooling:就是同上述一样,只不过取得是平均值呀!
(8)全连接层
详见这篇稿哦:小白学习machine learning的第二天-优快云博客
二、卷积神经网络的训练
(1)基本方法:利用链式求导计算损失函数对每个权重的偏导数(梯度),然后根据梯度下降公式更新权重。训练算法依然是反向传播算法。下面这张图是回顾哦!
(2)具体看看每一层的变化
①卷积层:
(i)卷积层误差项的传递:

Wl表示第l层的filter的权重数组
那么最后可以得到在步长为1的情况下,有如下这个卷积的公式:
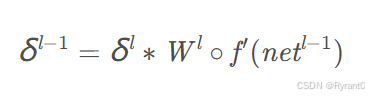
卷积步长为S时的误差传递:步长为S的sensitivity map相应的位置进行补0(zero padding大家还记得嘛),将其”还原“成步长为1时的sensitivity map,再用上述式子进行求解呀。
输入层深度为D时的误差传递:输入深度为D时,filter的深度也必须为D喔,那么l−1层的di通道只与filter的di通道的权重进行计算。(有图有真相O(∩_∩)O)
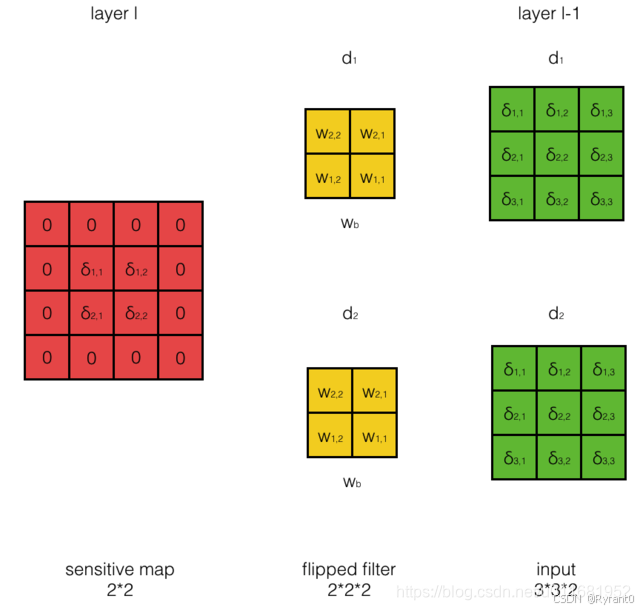
filter数量为N时的误差传递:filter数量为N时,输出层的深度也为N。其实就是用第d个filter对第l层相应的第d个sensitivity map进行卷积 ——>有n个l-1层的sensitivity map——>每个filter都做一次——>得到d组sensitivity map!!!各组之间将n个sensitivity map 一格一格相加——>得到最终的n个l−1层的sensitivity map了。
下面看看公式怎么说:
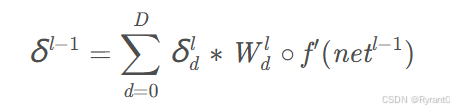
注:“。”是矩阵中每个对应元素相乘
(ii)卷积层filter权重梯度的计算:
其实就是计算![]() 。
。
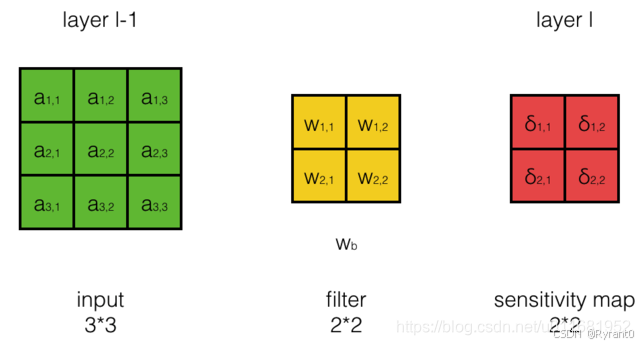
原文通过一番颇具想象力的数学公式推导,其实就是把wij对netij的影响进而对Ed的影响因子找到,然后发掘出这个公式:
梯度: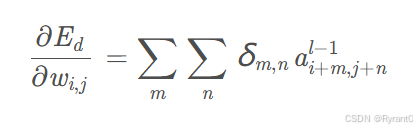
偏置项:(就是所有误差项的和)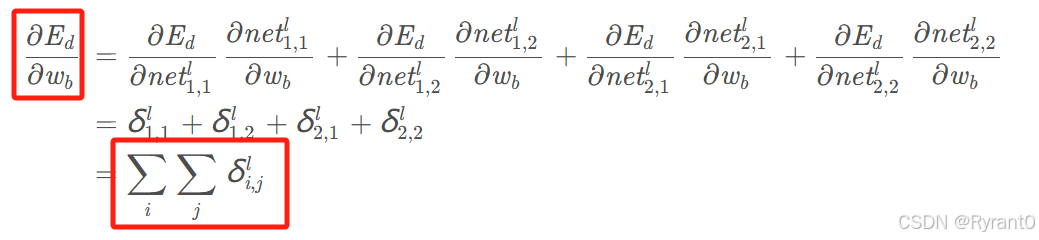
值得补充的一点是:(还好作者写了)当步长是s是,就一定要把你的sensitivity map还原成步长为1。可以通过插入0来解决喔。
②pooling 层:
最大池化(max pooling):省流,对于max pooling,下一层的误差项的值会原封不动的传递到上一层对应区块中的最大值所对应的神经元,而其他神经元的误差项的值都是0。
平均池化(mean pooling):对于mean pooling,下一层的误差项的值会平均分配到上一层对应区块中的所有神经元。
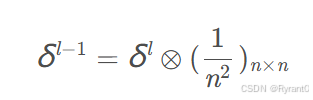 (克罗内克积形式)
(克罗内克积形式)
今天那就到这里吧,相信已经基本掌握了卷积神经网络的优势,训练算法,那么明天将进入最万众瞩目的实战代码环节以及循环神经网络啦!敬请期待呀 O(∩_∩)O





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








