小白学习machine learning的第二天

本篇的启发仍旧是来自下面这篇文章的学习呢！

零基础入门深度学习(3) - 神经网络和反向传播算法_零基础入门深度学习(三)-优快云博客

传送门：小白学习machine learning的第一天-优快云博客

                小白学习machine learning的第二天-优快云博客

                小白学习machine learning的第三天-优快云博客

                小白学习machine learning的第四天-优快云博客

                小白学习machine learning的第五天-优快云博客

                小白学习machine learning的第六天-优快云博客

我们首先来认识一下神经网络的计算方式：

（1）这是神经网络的示意图：

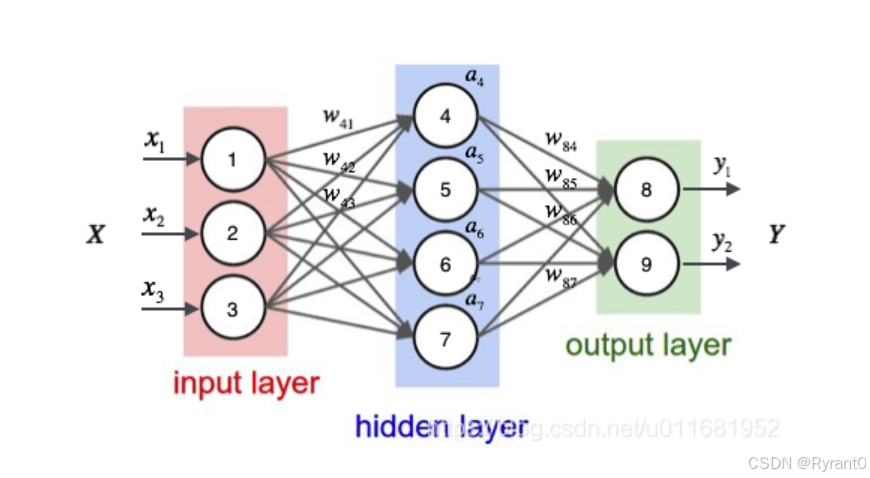
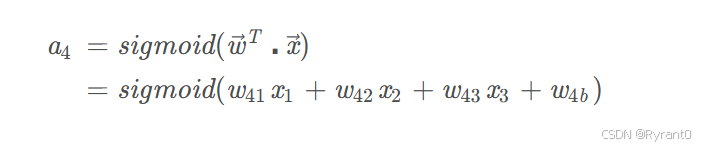
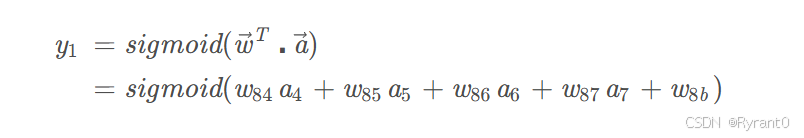
其实，原理就是：

1、每个神经层的所有输出值（eg.a1\a2\a3）（一般不这么写，一般写成多维向量乘上向量）

2、都乘上一个bias（偏差或称权值）后

3、再输给下一个层（eg.4号）

4、然后，再由4号的神经元计算给出输出值：a4 啦！！！

那么，借用原稿的话来说，就是我们换种逼格更高的写法——矩阵：

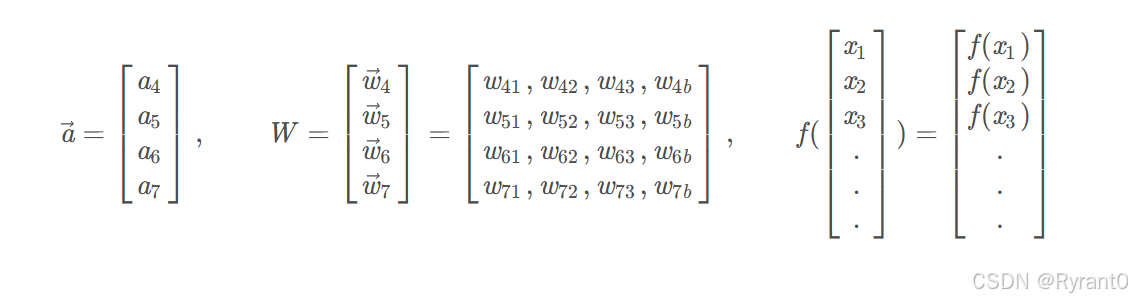
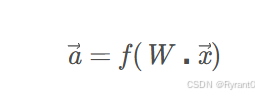
就有如下的计算向量a的式子出来啦！

———————————————————————————————————————————

我们再来个更复杂一点点的神经网络：

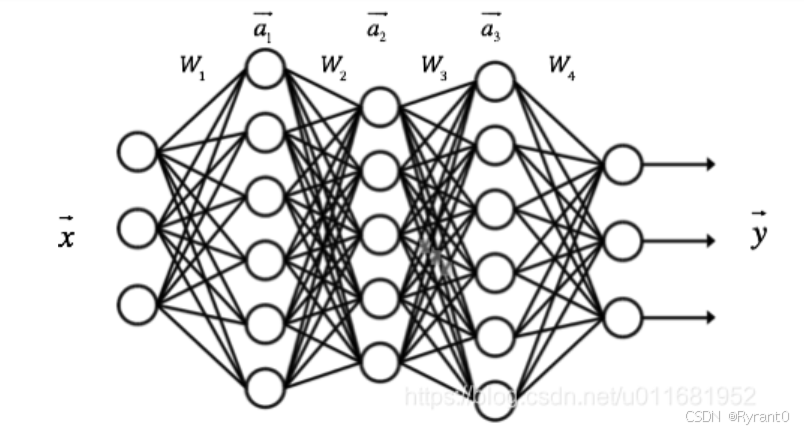
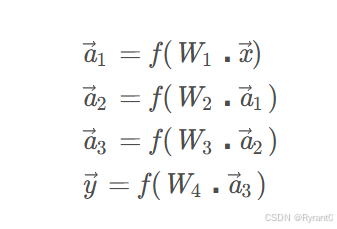
那么，计算结果的表达就是这样啦！其实大差不差的呢。

（2）下面是关于反向传播算法的学习啦

照用上图，我们用4和8两个节点来进行学习，首先需要掌握误差项δ i 的计算公式：

①对于隐藏层节点：

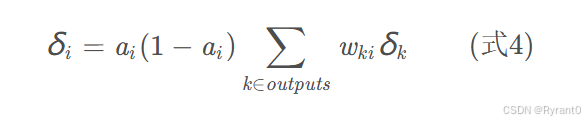
我们来详细看看，ai​​是节点的输出值，wki​是节点i到它的下一层节点k的连接的权重（注意有2个节点可变），δ k 是节点的下一层节点k的误差项（因为有下一个节点决定的变量，所以才是反向传播）。

举个栗子：

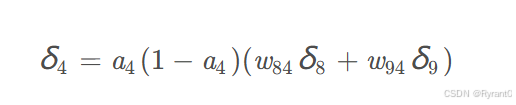
可以看到4与8和9都相连，所以8和9都要加。

②对于输出层节点（别忘了咋们是反向传播哦，所以要从屁股开始耶）：

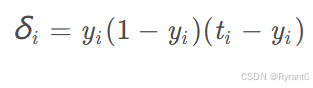
知道了误差项，那么就可以去更新权重wi了啦！

我们来看看：

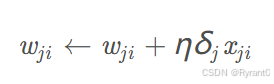
wji​是节点i到节点j的权重，η 是学习速率常数，δ j ​是节点j的误差项，xji​是节点i传递给节点j的输入。

注意的是：原文说到偏置项xji的值一直看作是1。误差项δ j 在有的文献中也叫做敏感度(sensitivity)。它实际上是网络的损失函数Ed​对神经元加权输入netj​的偏导数。

但是，根据激活函数是sigmoid函数、平方和误差、全连接网络、随机梯度下降优化算法才是上面的公式，而其他的激活函数则需要另外用数学公式链式求导法则得到（♂死我了这数学推导……）

*详见原文有推导过程哦！

（3）接下来，我们来看看原文的全连接神经网络是怎么实现的：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-

import random
from numpy import *

def sigmoid(inX):
    return 1.0 / (1 + exp(-inX))

class Node(object):
    def __init__(self, layer_index, node_index):
        self.layer_index = layer_index
        self.node_index = node_index
        self.downstream = []
        self.upstream = []
        self.output = 0
        self.delta = 0

    def set_output(self, output):
        self.output = output

    def append_downstream_connection(self, conn):
        self.downstream.append(conn)

    def append_upstream_connection(self, conn):
        self.upstream.append(conn)

    def calc_output(self):
        output = reduce(lambda ret, conn: ret + conn.upstream_node.output * conn.weight, self.upstream, 0)
        self.output = sigmoid(output)

    def calc_hidden_layer_delta(self):
        downstream_delta = reduce(
            lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
            self.downstream, 0.0)
        self.delta = self.output * (1 - self.output) * downstream_delta

    def calc_output_layer_delta(self, label):
        self.delta = self.output * (1 - self.output) * (label - self.output)

    def __str__(self):
        node_str = '%u-%u: output: %f delta: %f' % (self.layer_index, self.node_index, self.output, self.delta)
        downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
        upstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.upstream, '')
        return node_str + '\n\tdownstream:' + downstream_str + '\n\tupstream:' + upstream_str 

class ConstNode(object):
    def __init__(self, layer_index, node_index):
        self.layer_index = layer_index
        self.node_index = node_index
        self.downstream = []
        self.output = 1

    def append_downstream_connection(self, conn):
        self.downstream.append(conn)

    def calc_hidden_layer_delta(self):
        downstream_delta = reduce(
            lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
            self.downstream, 0.0)
        self.delta = self.output * (1 - self.output) * downstream_delta

    def __str__(self):
        node_str = '%u-%u: output: 1' % (self.layer_index, self.node_index)
        downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
        return node_str + '\n\tdownstream:' + downstream_str

class Layer(object):
    def __init__(self, layer_index, node_count):
        self.layer_index = layer_index
        self.nodes = []
        for i in range(node_count):
            self.nodes.append(Node(layer_index, i))
        self.nodes.append(ConstNode(layer_index, node_count))

    def set_output(self, data):
        for i in range(len(data)):
            self.nodes[i].set_output(data[i])

    def calc_output(self):
        for node in self.nodes[:-1]:
            node.calc_output()

    def dump(self):
        for node in self.nodes:
            print node

class Connection(object):
    def __init__(self, upstream_node, downstream_node):
        self.upstream_node = upstream_node
        self.downstream_node = downstream_node
        self.weight = random.uniform(-0.1, 0.1)
        self.gradient = 0.0

    def calc_gradient(self):
        self.gradient = self.downstream_node.delta * self.upstream_node.output

    def update_weight(self, rate):
        self.calc_gradient()
        self.weight += rate * self.gradient

    def get_gradient(self):
        return self.gradient

    def __str__(self):
        return '(%u-%u) -> (%u-%u) = %f' % (
            self.upstream_node.layer_index, 
            self.upstream_node.node_index,
            self.downstream_node.layer_index, 
            self.downstream_node.node_index, 
            self.weight)

class Connections(object):
    def __init__(self):
        self.connections = []

    def add_connection(self, connection):
        self.connections.append(connection)

    def dump(self):
        for conn in self.connections:
            print conn

class Network(object):
    def __init__(self, layers):
        self.connections = Connections()
        self.layers = []
        layer_count = len(layers)
        node_count = 0;
        for i in range(layer_count):
            self.layers.append(Layer(i, layers[i]))
        for layer in range(layer_count - 1):
            connections = [Connection(upstream_node, downstream_node) 
                           for upstream_node in self.layers[layer].nodes
                           for downstream_node in self.layers[layer + 1].nodes[:-1]]
            for conn in connections:
                self.connections.add_connection(conn)
                conn.downstream_node.append_upstream_connection(conn)
                conn.upstream_node.append_downstream_connection(conn)

    def train(self, labels, data_set, rate, epoch):
        for i in range(epoch):
            for d in range(len(data_set)):
                self.train_one_sample(labels[d], data_set[d], rate)
                # print 'sample %d training finished' % d

    def train_one_sample(self, label, sample, rate):
        self.predict(sample)
        self.calc_delta(label)
        self.update_weight(rate)

    def calc_delta(self, label):
        output_nodes = self.layers[-1].nodes
        for i in range(len(label)):
            output_nodes[i].calc_output_layer_delta(label[i])
        for layer in self.layers[-2::-1]:
            for node in layer.nodes:
                node.calc_hidden_layer_delta()

    def update_weight(self, rate):
        for layer in self.layers[:-1]:
            for node in layer.nodes:
                for conn in node.downstream:
                    conn.update_weight(rate)

    def calc_gradient(self):
        for layer in self.layers[:-1]:
            for node in layer.nodes:
                for conn in node.downstream:
                    conn.calc_gradient()

    def get_gradient(self, label, sample):
        self.predict(sample)
        self.calc_delta(label)
        self.calc_gradient()

    def predict(self, sample):
        self.layers[0].set_output(sample)
        for i in range(1, len(self.layers)):
            self.layers[i].calc_output()
        return map(lambda node: node.output, self.layers[-1].nodes[:-1])

    def dump(self):
        for layer in self.layers:
            layer.dump()

class Normalizer(object):
    def __init__(self):
        self.mask = [
            0x1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80
        ]

    def norm(self, number):
        return map(lambda m: 0.9 if number & m else 0.1, self.mask)

    def denorm(self, vec):
        binary = map(lambda i: 1 if i > 0.5 else 0, vec)
        for i in range(len(self.mask)):
            binary[i] = binary[i] * self.mask[i]
        return reduce(lambda x,y: x + y, binary)

def mean_square_error(vec1, vec2):
    return 0.5 * reduce(lambda a, b: a + b, 
                        map(lambda v: (v[0] - v[1]) * (v[0] - v[1]),
                            zip(vec1, vec2)
                        )
                 )

def gradient_check(network, sample_feature, sample_label):
    '''
    梯度检查
    network: 神经网络对象
    sample_feature: 样本的特征
    sample_label: 样本的标签
    '''
    # 计算网络误差
    network_error = lambda vec1, vec2: \
            0.5 * reduce(lambda a, b: a + b, 
                      map(lambda v: (v[0] - v[1]) * (v[0] - v[1]),
                          zip(vec1, vec2)))

    # 获取网络在当前样本下每个连接的梯度
    network.get_gradient(sample_feature, sample_label)

    # 对每个权重做梯度检查    
    for conn in network.connections.connections: 
        # 获取指定连接的梯度
        actual_gradient = conn.get_gradient()
    
        # 增加一个很小的值，计算网络的误差
        epsilon = 0.0001
        conn.weight += epsilon
        error1 = network_error(network.predict(sample_feature), sample_label)
    
        # 减去一个很小的值，计算网络的误差
        conn.weight -= 2 * epsilon # 刚才加过了一次，因此这里需要减去2倍
        error2 = network_error(network.predict(sample_feature), sample_label)
    
        # 根据式6计算期望的梯度值
        expected_gradient = (error2 - error1) / (2 * epsilon)
    
        # 打印
        print 'expected gradient: \t%f\nactual gradient: \t%f' % (
            expected_gradient, actual_gradient)

def train_data_set():
    normalizer = Normalizer()
    data_set = []
    labels = []
    for i in range(0, 256, 8):
        n = normalizer.norm(int(random.uniform(0, 256)))
        data_set.append(n)
        labels.append(n)
    return labels, data_set

def train(network):
    labels, data_set = train_data_set()
    network.train(labels, data_set, 0.3, 50)

def test(network, data):
    normalizer = Normalizer()
    norm_data = normalizer.norm(data)
    predict_data = network.predict(norm_data)
    print '\ttestdata(%u)\tpredict(%u)' % (
        data, normalizer.denorm(predict_data))

def correct_ratio(network):
    normalizer = Normalizer()
    correct = 0.0;
    for i in range(256):
        if normalizer.denorm(network.predict(normalizer.norm(i))) == i:
            correct += 1.0
    print 'correct_ratio: %.2f%%' % (correct / 256 * 100)

def gradient_check_test():
    net = Network([2, 2, 2])
    sample_feature = [0.9, 0.1]
    sample_label = [0.9, 0.1]
    gradient_check(net, sample_feature, sample_label)

if __name__ == '__main__':
    net = Network([8, 3, 8])
    train(net)
    net.dump()
    correct_ratio(net)

（4）那么，会写还不够，还得学会查出错误的地方，梯度检查是一个好办法：

①相当于检查每一个权重了：

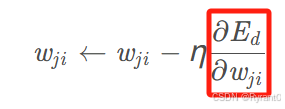
这里检查的是红框里的一定要合适正确！！！

根据原文的推导，我们得到这个式子。

把他右边计算出来跟神经网络代码中计算出来的梯度值进行比较，应该有4位数字相同。

②另外，我们可以检查参数wji​的梯度是否正确：

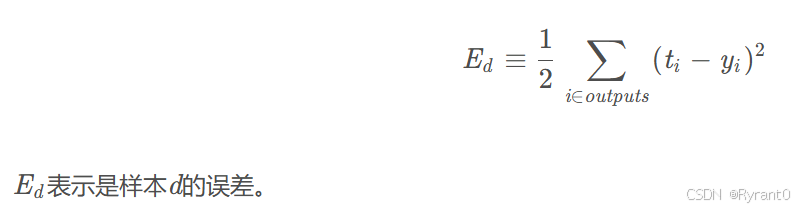
下面引用原文：

（5）那么，用识别手写字母来开启第一个神经网络项目，首先要学习怎么用“好手艺”来设置超参数：

首先来看看“经验学说”怎么看：

代码实现详见原文啦！

（6）从面向对象编程到向量化编程！

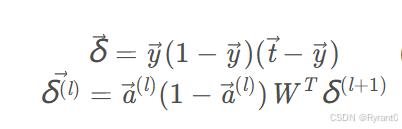
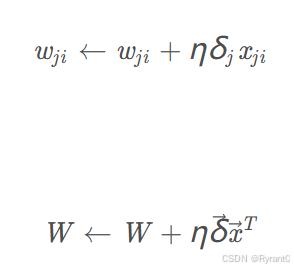
# 全连接层实现类
class FullConnectedLayer(object):
    def __init__(self, input_size, output_size, 
                 activator):
        '''
        构造函数
        input_size: 本层输入向量的维度
        output_size: 本层输出向量的维度
        activator: 激活函数
        '''
        self.input_size = input_size
        self.output_size = output_size
        self.activator = activator
        # 权重数组W
        self.W = np.random.uniform(-0.1, 0.1,
            (output_size, input_size))
        # 偏置项b
        self.b = np.zeros((output_size, 1))
        # 输出向量
        self.output = np.zeros((output_size, 1))
    def forward(self, input_array):
        '''
        前向计算
        input_array: 输入向量，维度必须等于input_size
        '''
        # 式2
        self.input = input_array
        self.output = self.activator.forward(
            np.dot(self.W, input_array) + self.b)
    def backward(self, delta_array):
        '''
        反向计算W和b的梯度
        delta_array: 从上一层传递过来的误差项
        '''
        # 式8
        self.delta = self.activator.backward(self.input) * np.dot(
            self.W.T, delta_array)
        self.W_grad = np.dot(delta_array, self.input.T)
        self.b_grad = delta_array
    def update(self, learning_rate):
        '''
        使用梯度下降算法更新权重
        '''
        self.W += learning_rate * self.W_grad
        self.b += learning_rate * self.b_grad

这个类一举取代了原先的Layer、Node、Connection等类，不但代码更加容易理解，而且运行速度也快了几百倍。

  现在，我们对Network类稍作修改，使之用到FullConnectedLayer：

_____________________________________________________________________________

# Sigmoid激活函数类
class SigmoidActivator(object):
    def forward(self, weighted_input):
        return 1.0 / (1.0 + np.exp(-weighted_input))
    def backward(self, output):
        return output * (1 - output)
# 神经网络类
class Network(object):
    def __init__(self, layers):
        '''
        构造函数
        '''
        self.layers = []
        for i in range(len(layers) - 1):
            self.layers.append(
                FullConnectedLayer(
                    layers[i], layers[i+1],
                    SigmoidActivator()
                )
            )
    def predict(self, sample):
        '''
        使用神经网络实现预测
        sample: 输入样本
        '''
        output = sample
        for layer in self.layers:
            layer.forward(output)
            output = layer.output
        return output
    def train(self, labels, data_set, rate, epoch):
        '''
        训练函数
        labels: 样本标签
        data_set: 输入样本
        rate: 学习速率
        epoch: 训练轮数
        '''
        for i in range(epoch):
            for d in range(len(data_set)):
                self.train_one_sample(labels[d], 
                    data_set[d], rate)
    def train_one_sample(self, label, sample, rate):
        self.predict(sample)
        self.calc_gradient(label)
        self.update_weight(rate)
    def calc_gradient(self, label):
        delta = self.layers[-1].activator.backward(
            self.layers[-1].output
        ) * (label - self.layers[-1].output)
        for layer in self.layers[::-1]:
            layer.backward(delta)
            delta = layer.delta
        return delta
    def update_weight(self, rate):
        for layer in self.layers:
            layer.update(rate)
到这里就结束啦！！！请等待下一次更新哦哈哈