倍增、RMQ

1. 倍增思想

（1）什么是倍增

        倍增法（英语：binary lifting ），顾名思义就是翻倍。他能够使线性的处理转化为对数级的处理，大大的优化时间复杂度。

        这个方法在很多算法中均有应用，其中最常用的是：RMQ 问题和求 LAG（最近公共祖先）。

        倍增思想是一种十分巧妙的思想。“倍增”二字体现在它每次将当前的已知结果或考察范围扩大一倍。正是由于这个原因，它的时间复杂度降低了很多，一般是将一个系数 N 变为 。

（2）倍增思想举例

        例子 1：如果要求比 n 小的最近的 2 的幂，，这个值，是从 1 开始跳跃 次得到的，这体现了倍增的思想。

        例子 2：

        如何用尽可能少的砝码称量出 [ 0 , 31 ] 之间的所有重量？（只能在天平的一端放砝码）

        答案是使用 1 2 4 8 16 这五个砝码，可以称量出 [ 0 , 31 ] 之间的所有重量。同样，如果要称量 [ 0 , 127 ] 之间的所有重量，可以使用 1 2 4 8 16 32 64 这七个砝码。每次我们都选择 2 的整次幂作为砝码的重量，就可以使用极少的砝码个数量出任意我们所需要的重量。

        可以发现，我们的目标量翻倍的情况下，我们需要的砝码数量只需要 +1。

        例子 3：

        有非负整数数列：a1 a2 a3 a4 a5 ... an，有 M 次询问，每次需要求：不超过给定的整数 Ti 的最大的前缀和。

        求解思路：预处理前缀和，倍增思想跳跃取值。

2. RMQ 问题

（1）RMQ 的解释

        RMQ（Range Maximum Query），用于静态区间最大值（也可以求最小值）。

        ST 表（Sparse Table，稀疏表）实现 RMQ 可以做到： 的预处理，O（1）的时间复杂度查询。用于多次询问 RMQ 的问题。特别注意：ST 的算法条件是数组本身不能有修改。

        ST 表是用于解决可重复贡献问题的数据结构。

（2）RMQ 的求解思想

        以每个点为左端点，求出长度为  的区间最大值。左端点的选择有 n 种，长度的选择有：1 2 4 ... ，也就是  种需要讨论的状态。

        这里采用 DP+ 倍增的思想求出从每个点开始的区间长度为  的区间最值。

        第一步：求 ST 表

 

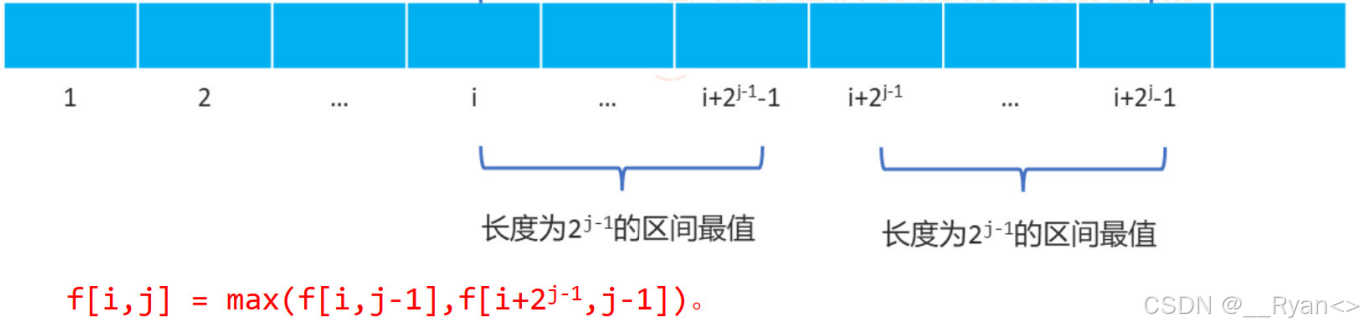
        第二步：区间询问

        询问 [ l , r ] 之间的区间最值。