Geogebra 绘制 电磁波反射&折射+斯涅尔定律+半波损失+阻抗匹配

Geogebra 绘制 电磁波反射&折射

• 均匀平面波转化到二维视角绘制电磁波反射&折射

• 仅当电磁波从光疏介质入射到光密介质的分界面，且为 “正入射”（入射角≈0°）或 “掠入射”（入射角≈90°）时，反射波会产生半波损失。

特性	斯涅尔定律 (Snell’s Law)	半波损失 (Half-Wave Loss)
领域	几何光学	波动光学
描述对象	光线的传播方向	光波的相位
核心参数	入射角、折射角、折射率	折射率、相位突变(π)
决定因素	两种介质的折射率 n₁, n₂	反射点处，反射侧介质的折射率是否更大
关键公式	n₁sinθ₁ = n₂sinθ₂	Δφ = π (当 n_入射 < n_反射 时)

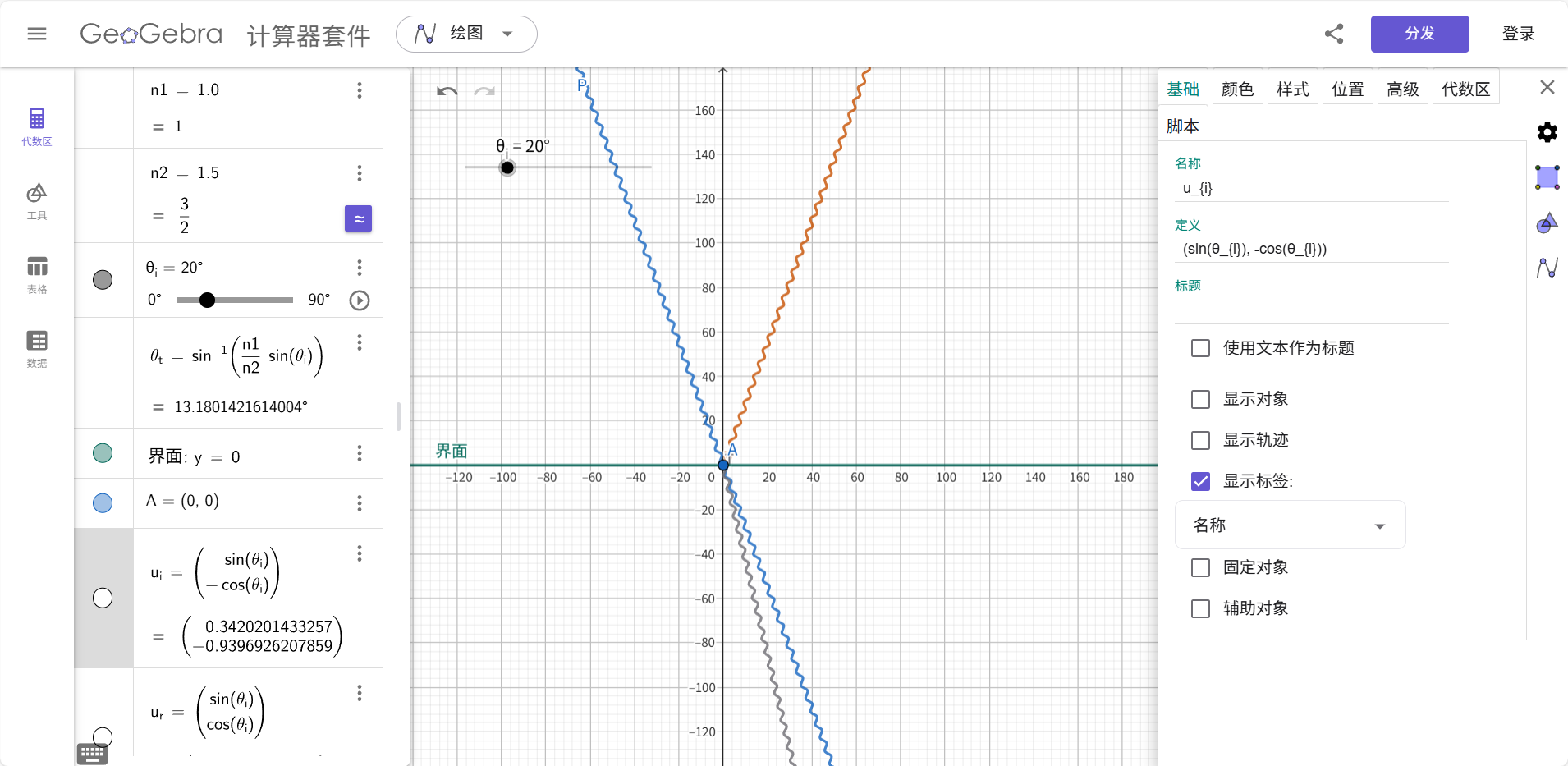
• 反射时的相位突变：
  

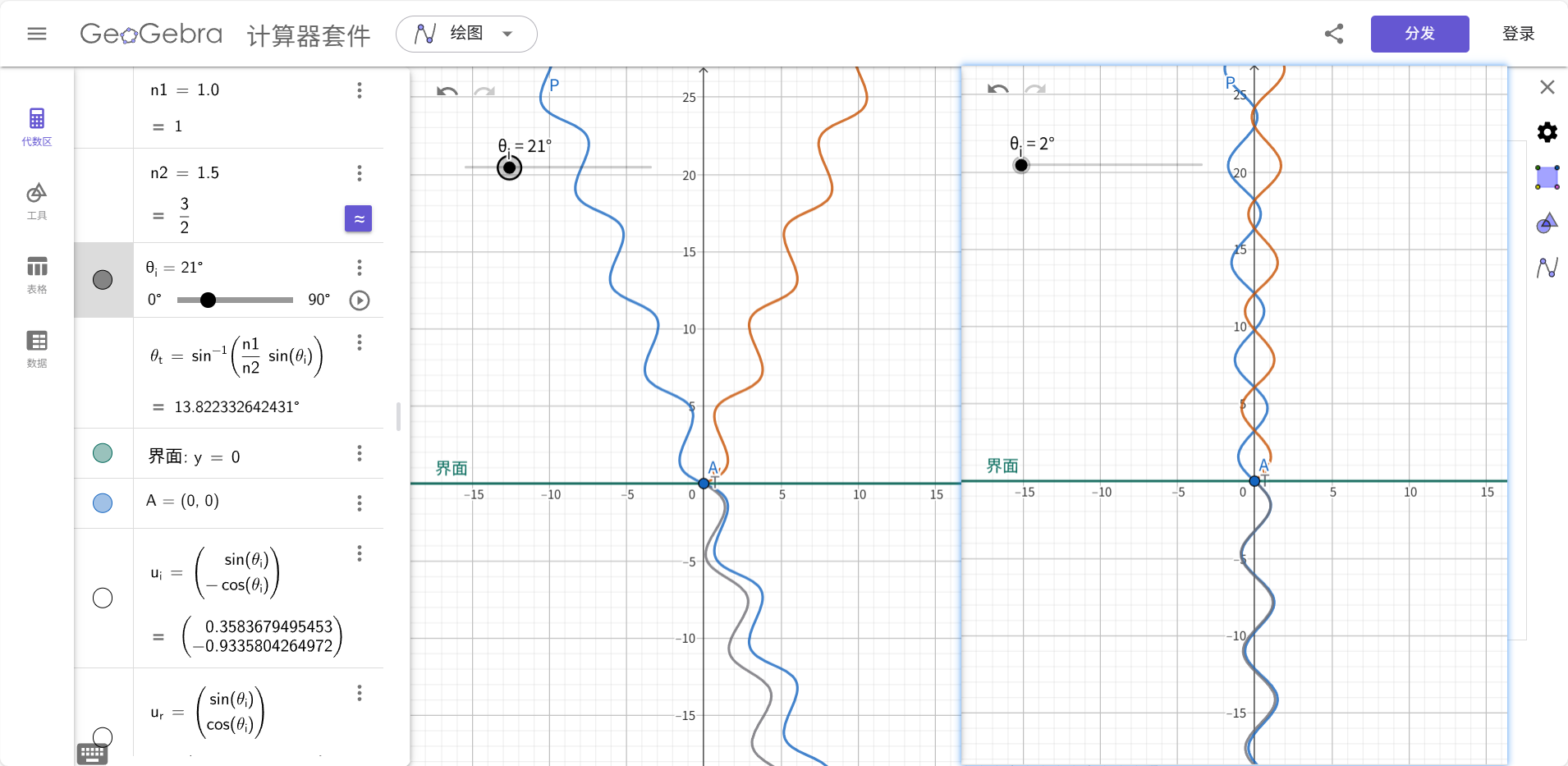
n1 = 1.0
n2 = 1.5
θ_i = 30°
θ_t = asin((n1 / n2) * sin(θ_i))
界面: y = 0
A = (0, 0)

u_i = (sin(θ_i), -cos(θ_i))
u_r = (sin(θ_i), cos(θ_i))
u_t = (sin(θ_t), -cos(θ_t))

v_i = (cos(θ_i), sin(θ_i))
v_r = (cos(θ_i), -sin(θ_i))
v_t = (cos(θ_t), sin(θ_t))


P=曲线(s u_i + sin(s) v_i,s,-200,200)
V=曲线(s u_r + -sin(s+pi) v_r,s,0,200)
T=曲线(s u_t + sin(s) v_t,s,0,200)

CG

• 变压器的阻抗匹配作用
• 什么是阻抗匹配？如何在设计中使用阻抗匹配变压器