Geogebra 绘制 均匀平面波 + TEM波

Geogebra 绘制 均匀平面波

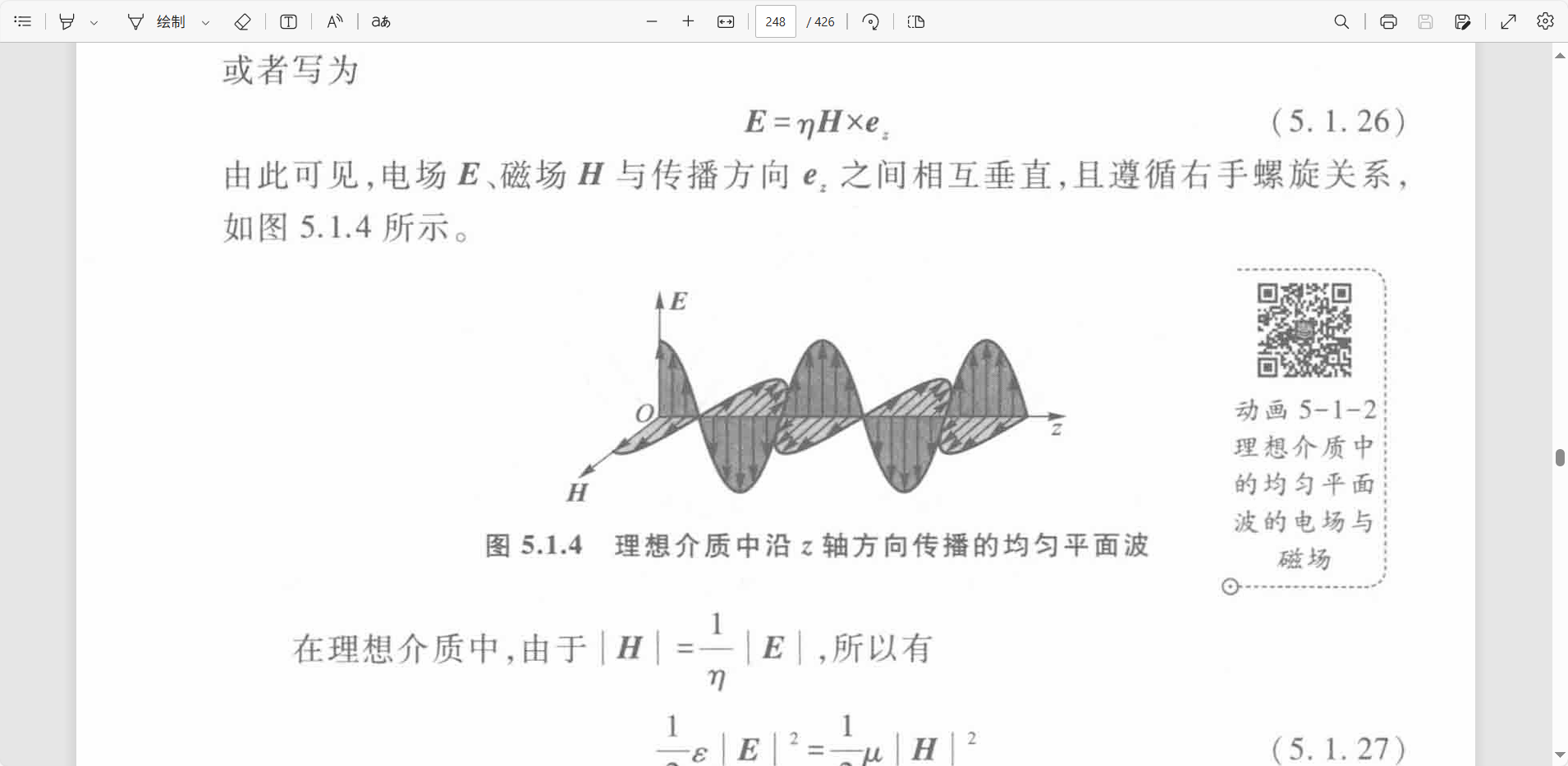
• 均匀平面波是横电磁波（TEM波），对于传输方向而言，电场和磁场只有横向分量，没有纵向分量，郑重平面电磁波篇被称为横电磁波，简写为TEM波。

  • 根据麦克斯韦第一方程：电场只有$E_x$和$E_y$分量，说明电场矢量位于xOy平面上。
  • 根据麦克斯韦第二方程：电场只有$H_x$和$H_y$分量，说明磁场矢量位于xOy平面上。
  • 详细证明见：《电磁场与电磁波》，参考书籍为《电磁场与电磁波（第5版）谢处方等》
  • 
    

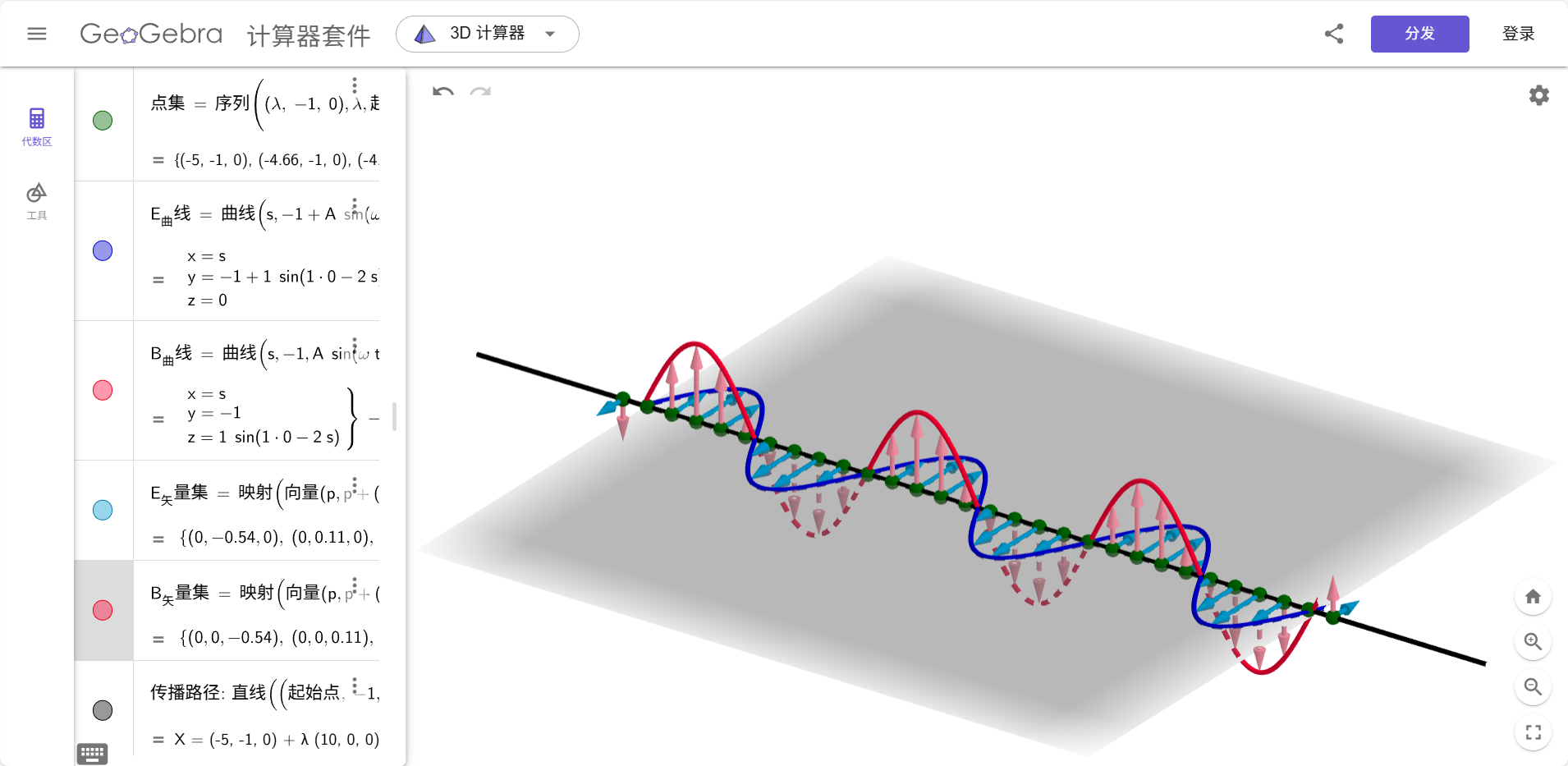
• 均匀平面波：

  • 电场 $E$ 在 y 轴方向振动
  • 磁场 $B$ 在 z 轴方向振动
  • 波动沿 x 方向传播
  • 时间上同相（相位差为 0）
  • E ⊥ B ⊥ 传播方向

k_x = 2
ω = 1
t = 0
A = 1
采样数 = 30
起始点 = -5
结束点 = 5

点集 = 序列( (λ, -1, 0), λ, 起始点, 结束点, (结束点 - 起始点) / (采样数 - 1) )
E = Zip(向量(p, p + (0, A * sin(ω * t - k_x * x(p)), 0), p, 点集)


E_矢量集 = Zip( 向量( p, p + (0, A * sin(ω * t - k_x * x(p)), 0) ), p, 点集 )
B_矢量集 = Zip( 向量( p, p + (0, 0, A * sin(ω * t - k_x * x(p))) ), p, 点集 )

B_曲线 = 曲线( s, -1, A * sin(ω * t - k_x * s), s, 起始点, 结束点 )


传播路径 = 直线((起始点, -1, 0), (结束点, -1, 0))

• 注：在真空中，电磁波的电场和磁场振幅大小关系为 E₀ = c * B₀，但为了可视化清晰，省略常数 c，让磁场和电场具有可比拟的振幅。