考虑著名的Steiner Tree问题:
问题描述
设
G
(
V
,
E
,
W
)是一个无向带权连通图
(
V
是顶点的集合,
E
是边的集合,
W
是边上权重的集合,顶点
v
i
,
v
j
∈
V
,由
v
i
,
v
j
构成的边记为
e
i
j
或者
e
j
i
,
边上的权重记为
w
i
j
或者
w
j
i
,
且
w
i
j
=
w
j
i
,
w
i
j
>
0
)
。
设G(V,E,W)是一个无向带权连通图\\ \tiny(V是顶点的集合,E是边的集合,W是边上权重的集合,顶点v_i,v_j∈V,由v_i,v_j构成的边记为e_{ij}或者e_{ji},边上的权重记为w_{ij}或者w_{ji},且w_{ij}=w_{ji},w_{ij}>0)。
设G(V,E,W)是一个无向带权连通图(V是顶点的集合,E是边的集合,W是边上权重的集合,顶点vi,vj∈V,由vi,vj构成的边记为eij或者eji,边上的权重记为wij或者wji,且wij=wji,wij>0)。
设
R
是
V
的一个子集,即
R
⊆
V
,在
G
中求一颗生成树
T
,使得
T
包含
R
中所有顶点,且生成树
T
的权重最小
(生成树
T
的权重是指构成
T
的所有边权重之和),即
m
i
n
{
∑
e
i
j
∈
T
w
i
j
}
权重最小的生成树
T
称为
G
关于
R
的
S
t
e
i
n
e
r
T
r
e
e
.
设R是V的一个子集,即R⊆V,在G中求一颗生成树T,使得T包含R中所有顶点,且生成树T的权重最小\\ (生成树T的权重是指构成T的所有边权重之和),即 min\{\sum_{e_{ij}\in T} w_{ij}\}\\ 权重最小的生成树T称为G关于R的Steiner Tree.
设R是V的一个子集,即R⊆V,在G中求一颗生成树T,使得T包含R中所有顶点,且生成树T的权重最小(生成树T的权重是指构成T的所有边权重之和),即min{eij∈T∑wij}权重最小的生成树T称为G关于R的SteinerTree.
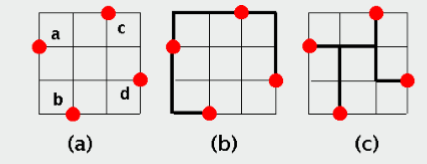
NPC证明
方法:
b
y
t
r
a
n
s
f
o
r
m
i
n
g
a
n
o
t
h
e
r
k
n
o
w
n
N
P
−
c
o
m
p
l
e
t
e
p
r
o
b
l
e
m
t
o
i
t
方法:by\ transforming\ \ another \ \ known\ \ NP-complete \ problem \ to \ it
方法:by transforming another known NP−complete problem to it
show that a problem Π is NP-complete:
- show than Π is in NP;\
- select a known NP-complete problem Π0;
- construct a transformation f from Π0 to Π;
- prove that f is a polynomial transformation.
Steiner Tree is in NP
假设存在正确解T,我们可以在多项式时间内验证:
T是一棵树,是联通的且不存在环
T包含顶点集合R的所有元素
树的边数不超过k
XKC问题 集合覆盖问题(选择最少的集合,覆盖所有的元素)
添加链接描述
XKC中k的意思是每个小集合只有三个元素
最小生成树是在给定的点集和边中寻求最短网络使所有点连通
而最小斯坦纳树允许在给定点外增加额外的点,使生成的最短网络开销最小





















 1281
1281

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








