深度学习笔记007：让训练更加稳定:模型初始化+激活函数(RELU)+梯度裁剪

FakeOccupational

已于 2022-02-13 09:09:19 修改

阅读量635

点赞数 1

CC 4.0 BY-SA版权

分类专栏：深度学习文章标签：深度学习 pytorch 机器学习

于 2021-07-09 18:16:19 首次发布

本文链接：https://blog.youkuaiyun.com/ResumeProject/article/details/118527226

深度学习专栏收录该内容

175 篇文章

订阅专栏

$合理的权重初始化和激活函数可提升数值稳定性。$

激活函数

RELU家族

RELU：ReLu不会对数据做幅度压缩，所以数据的幅度会随着模型层数的增加不断扩张

torch.nn.ReLU(inplace=False)

Leaky-ReLU：不会坏死神经元

torch.nn.LeakyReLU(negative_slope=0.01,inplace=False)

参数化修正线性单元（PReLU）：负值部分的斜率是根据数据来定的，而非预先定义的。ImageNet上，PReLU是超越人类分类水平的关键所在。

torch.nn.PReLU(num_parameters=1,init=0.25)
其中a 是一个可学习的参数，当不带参数调用时，即nn.PReLU()，在所有的输入通道上使用同一个a，当带参数调用时，即nn.PReLU(nChannels)，在每一个通道上学习一个单独的a。

随机纠正线性单元（RReLU）：斜率为均匀的分布U(I,u)中随机抽取的数值。官网链接

m = nn.RReLU(0.1, 0.3)
input = torch.randn(2)
output = m(input)

其他激活函数

Sigmoid激活函数

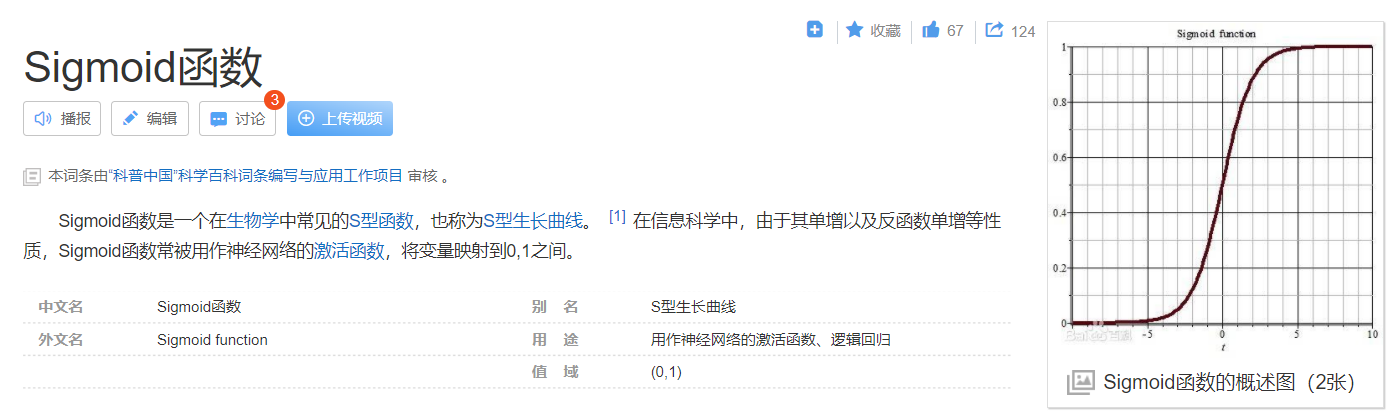
在这里插入图片描述

$使用昨天的记忆s_{t-1}和今天的输入x_t进行长期记忆c_t的删除操作$

Tanh / 双曲正切激活函数

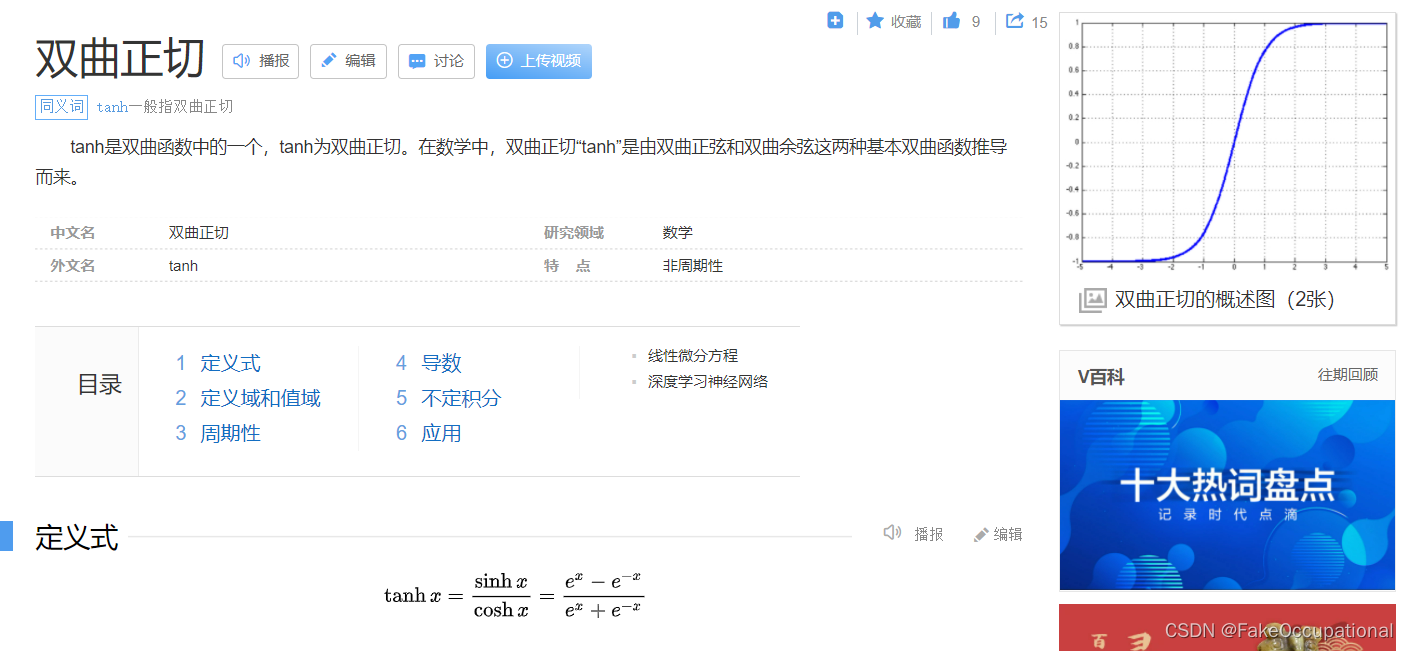
在这里插入图片描述
LSTM 中为什么要用 tanh 激活函数？tanh 激活函数的作用及优势在哪里？

在这里插入图片描述
$在更新门中使用了 t a n h, 对特征进行重新整理和归纳。$

Softmax：使用其特性进行注意力计算中的“掩码”操作

在这里插入图片描述

Swish

Maxout：只有 2 个 maxout 节点的多层感知机就可以拟合任意的凸函数

Softplus：平滑过渡的RELU

模型初始化

在这里插入图片描述
$让每一层的输出和梯度均值为零方差固定的随机 b i a a n l i n g$

iid :独立通分布

$即若输入的方差和输出的方差一样的话：n_{t-1} * γ_t=1$
反向类似：

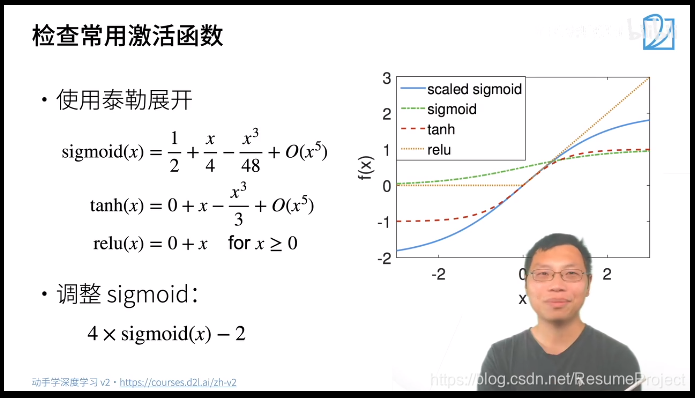
在这里插入图片描述

$其中n_{t-1}(第t层输入的维度)和n_{t}(第t层输出的维度)是我们不能控制的$
在这里插入图片描述
下边看看激活函数的设置，刚才假设没有激活函数，现在为了分析方便假设是线性的激活函数：

$意味着激活函数应该是 σ (x) = x$

$下边两个函数能够满足在0附近满足要求(神经网络权重等值一般就是0点附近),\\所以可对sigmod进行调整$

梯度裁剪

torch.nn.utils.clip_grad_norm(parameters, max_norm, norm_type=2)

即将梯度的数值限制在一定的阈值之中。

import torch
a = torch.rand(3,3) * 10
b = a.clamp(-5,5)
print(a,'\n',b)

tensor([[3.2108, 3.9465, 5.8162],
        [5.2172, 8.7149, 6.7542],
        [7.5422, 5.3353, 7.6233]]) 
 tensor([[3.2108, 3.9465, 5.0000],
        [5.0000, 5.0000, 5.0000],
        [5.0000, 5.0000, 5.0000]])