P1886 滑动窗口 /【模板】单调队列

最新推荐文章于 2025-09-29 19:23:09 发布

原创最新推荐文章于 2025-09-29 19:23:09 发布 · 169 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

洛谷专栏收录该内容

129 篇文章

订阅专栏

该博客介绍了如何使用C++实现一个算法，解决给定序列a中长度为k的窗口滑动时的最大值和最小值问题。通过维护两个队列来高效跟踪窗口内的极值，适用于大规模数据范围的场景。

题目描述

有一个长为 n 的序列 a，以及一个大小为 k 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1,3,-1,-3,5,3,6,7], andk=3。

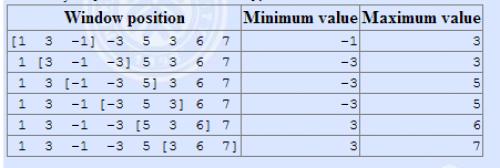
输入格式

输入一共有两行，第一行有两个正整数 n,k。第二行 n 个整数，表示序列 a

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

输入输出样例

输入 #1

8 3
1 3 -1 -3 5 3 6 7

输出 #1

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明/提示

【数据范围】
对于50% 的数据，1≤n≤105；
对于100% 的数据，1≤k≤n≤10^6

/*
 * @Description: To iterate is human, to recurse divine.
 * @Autor: Recursion
 * @Date: 2022-03-06 22:36:34
 * @LastEditTime: 2022-03-06 23:49:24
 */
#include<bits/stdc++.h>
using namespace std;
int n,k,x,m[(int)1e6+10];
int cnt=0;
int maxnn[(int)1e6+10];//x,y 数组用来存答案
int minnn[(int)1e6+10];
struct node
{
    int order;
    int value;
};

deque<node> maxn,minn;

int main()
{
    while(cin>>n>>k){
        node temp;//暂时储存
        for(int i=1;i<=n;i++){
            cin>>x;

            temp.order=i;
            temp.value=x;//赋值
            
            while(!maxn.empty()&&x>=maxn.back().value)
                maxn.pop_back();
            while(!minn.empty()&&x<=minn.back().value)
                minn.pop_back();//保证队列单调
                
            maxn.push_back(temp);
            minn.push_back(temp);

            while(i-k>=maxn.front().order)//剔除不在范围类的
                maxn.pop_front();
            while(i-k>=minn.front().order)
                minn.pop_front();

            if(i>=k){
                maxnn[cnt]=maxn.front().value;
                minnn[cnt]=minn.front().value;
                cnt++;
            }
        }
        for(int i=0;i<cnt;i++)
            cout<<minnn[i]<<" ";
        cout<<endl;
        for(int i=0;i<cnt;i++)
            cout<<maxnn[i]<<" ";
        // for(int i=1;i<=n-k+1;i++){
        //     int maxx=a[i];
        //     int minn=a[i];
        //     for(int j=i;j<i+k;j++){
        //         if(a[j]<=minn)
        //             y[i]=a[j];
        //         if(a[j]>=maxx)
        //             x[i]=a[j];
        //     }
        // }
        // for(int i=1;i<=n-k+1;i++)
        //     cout<<x[i]<<" ";
        // cout<<endl;
        // for(int i=1;i<=n-k+1;i++)
        //     cout<<y[i]<<" ";
    }
    return 0;
}