算法Tips1--一维数组前缀和

一维数组前缀和

---

为什么使用前缀和？

前缀和技巧适用于快速、频繁地计算一个索引区间的元素之和

---

例题一：区域和检索-数组不可变

乍一看这简单，直接暴力穷举遍历就完了，确实解决问题
看一眼代码，没问题的！

普通解法：

// 时间复杂度为O(n)
    static class NumArray1{
        private int[] nums;
        public NumArray1 (int[] nums){
            this.nums = nums;
        }
        public int SumRange(int left,int right){
            int res=0;
            for(int i=left;i<=right;i++){
                res+=nums[i];
            }
            System.out.println("数组"+left+"-"+right+"区间和为"+res);
            return res;
        }
    }

优化解法：

使用前缀和数组，就是在初始化数组的同时，计算前n个数组元素的和，形成一个新的数组，这样非常方便之后频繁的数组进行区域求和

//时间复杂度为O(1)
    static class NumArray{

        private int[] preSum;
        NumArray(int[] nums){
            //preSum[0]=0 便于计算累加和
            preSum = new int[nums.length+1];
            for(int i=1;i<nums.length;i++){
                preSum[i] = preSum[i-1]+nums[i-1];     //构造出前缀和数组 ，nums的索引从0开始所以也是i-1
            }
            for(int i:preSum)   System.out.print(i+" ");
        } 
        public void SumRange(int left,int right){
            int res = preSum[right+1]-preSum[left]; //preSum第一个是0，索引要加1
            System.out.println("区间和为："+res);
        }
    }

注意到，上面是形成一个新的前缀和数组，其实还可以根据本身的数组计算前缀和，具体问题具体分析哦！

• 下面这个例子是计算考试成绩分数段的

//查询分数段
    public void SearchFunc(){
        int [] scores={100,99,80,88,54,60,44,89,72,74,23};
        int[] count = new int[scores.length+1];  
        for(int score:scores)   count[score]++;

        for(int i=1;i<scores.length;i++)
            count[i]=count[i]+count[i-1]; //自身数组构造
    } 

例题二：二维区域和检索 - 矩阵不可变

举个栗子，也就是如何计算下面这个矩阵中的红色区域：

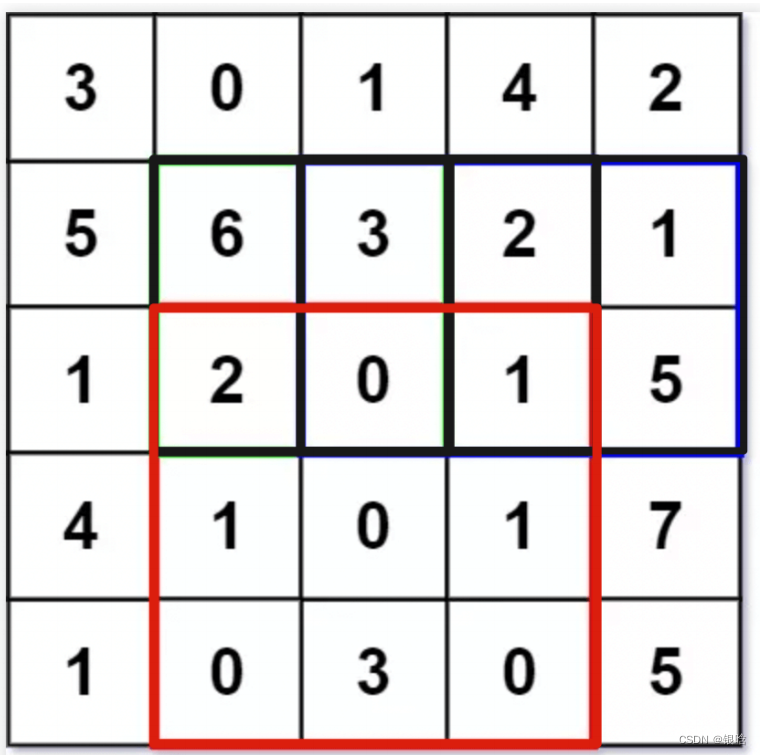
• 核心思想：加减来凑
• 记住 目标矩阵 = 大矩阵 - 左侧留余的矩阵 - 上侧留余的矩阵 + 重叠部分矩阵

如下图我标出来的矩阵：

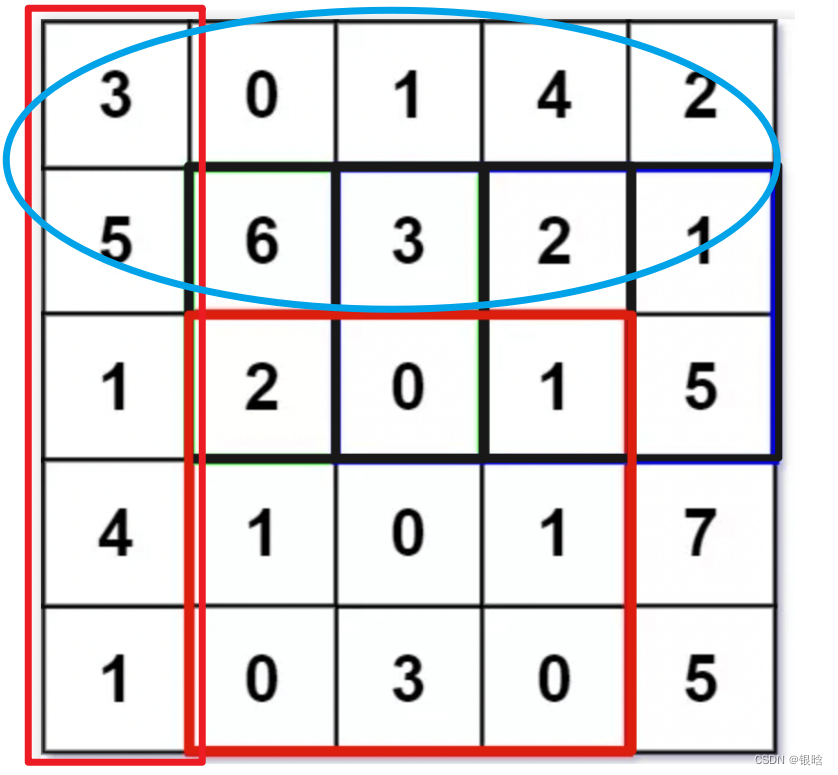
思想清楚了，话不多说，看代码

 //二维区域和
    static class NumMatrix{

        private int[][] preSum;
        NumMatrix(int[][] matrix){
            int m = matrix.length; int n = matrix[0].length;
            if(m==0||n==0)  return ;

            //构造前缀和矩阵
            preSum = new int[m+1][n+1];

            for(int i=1;i<m;i++)
                for(int j=1;j<n;j++){
                    preSum[i][j] = preSum[i-1][j]+preSum[i][j-1]+matrix[i][j]-preSum[i-1][j-1];
                    //左+右+新值-重叠
                }
        }
        public int SumMatrix(int x1,int x2,int y1,int y2){
            //大矩阵 - 左边缘 - 上边缘 + 重叠
            int res = preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
            return res;
        }
    }

例题三、和为k的子数组

咋一看题目，一想 if (preSum[i]-preSum[j]==k) 就完事了，刚刚学了前缀和，嗯挺不错的哦！

//和为k的子数组
    void sunArray(int[] nums,int k){
        int n=nums.length;
        int res=0;
        //构造前缀和
        int[] preSum = new int [n+1];
        for(int i = 1;i<nums.length;i++){
            preSum[i] = preSum[i-1]+nums[i-1];
        }

        //穷举法
        for(int i=1;i<=n ;i++)
            for(int j=0;j<i;j++){
                if(preSum[i]-preSum[j]==k)
                    res++;
            }
    }

但是呢，我们不能止步于此，说实话我第一次看到还能再优化的方法，只能感慨智商不太够了，呜呜呜~

这个解法的时间复杂度 O(N^2) 空间复杂度 O(N)，并不是最优的解法。不过通过这个解法理解了前缀和数 组的⼯作原理之后，可以使⽤⼀些巧妙的办法把时间复杂度进⼀步降低。

优化

void hashmapSum(int[] nums,int k){
         //哈希表优化,优化思路，避免内层的循环判断，直接更新结果
        //map:前缀和 -> 出现次数
        HashMap<Integer,Integer> Presum = new HashMap<>();  
        Presum.put(0, 1);
        int res=0 ,sum_i=0,n=nums.length;
        for(int i=0;i<n;i++){
            sum_i +=nums[i];
            int sum_j=sum_i -k;

            if(Presum.containsKey(sum_j))   //哈希表查找有没有这个前缀和
                res+=Presum.get(sum_j);
            Presum.put(sum_i, Presum.getOrDefault(sum_i, 0)+1); //有值get返回1，没有就是0
        }
    }

• 运用了哈希表的快速索引的特性，来减小第二个for循环的时间复杂度，从而提高整个算法的效率

总结

唉，兄弟们，慢慢来吧，反正题都写不出来，看答案总能看得懂，开摆开摆~