AcWing第一章算法模板总结——基础算法

一、排序算法
二、二分
三、高精度
四、前缀
五、差分
六、位运算
七、双指针算法
八、离散化
九、区间合并

一、排序算法

（一）快速排序算法

时间复杂度：最好O(nlog₂n) 平均O(nlog₂n) 最差O(n²)
空间复杂度：O(log₂n)
具有稳定性

主要思想是分治
1、首先找到枢纽元素pivot，一般取左边界元素
2、指定指针i为左边界，指针j为右边界，分别向右向左遍历扫描，如果满足q[i]>pivot且q[j]<pivot,交换q[i]和q[j]元素，此步操作为了保证在pivot元素左边的值必须小于等于pivot，处于pivot右边的元素必须大于等于pivot。直到不满足i<j
3、递归处理pivot的左右两边

模板：

void Quicksort(int* q, int l, int r)
{
   
   
    if (l >= r) return;

    int pivot = q[l], i = l - 1, j = r + 1;
    while(i < j)
    {
   
   
        do i++; while(q[i] < pivot);
        do j--; while(q[j] > pivot);
        if(i < j) swap(q[i], q[j]);
    } 

	/*
	这里需要注意,如果使用i作为中间索引的话，则上面pivot的取值不能取q[l],否则会出现死循环,即：
	Quicksort(q, l, i);
    Quicksort(q, i - 1, r);
	
	*/
    Quicksort(q, l, j);
    Quicksort(q, j + 1, r);
}

（二）归并排序算法

时间复杂度：最好O(nlog₂n) 平均O(nlog₂n) 最差O(nlog₂n)
空间复杂度：O(n)
具有稳定性，且稳定性最好

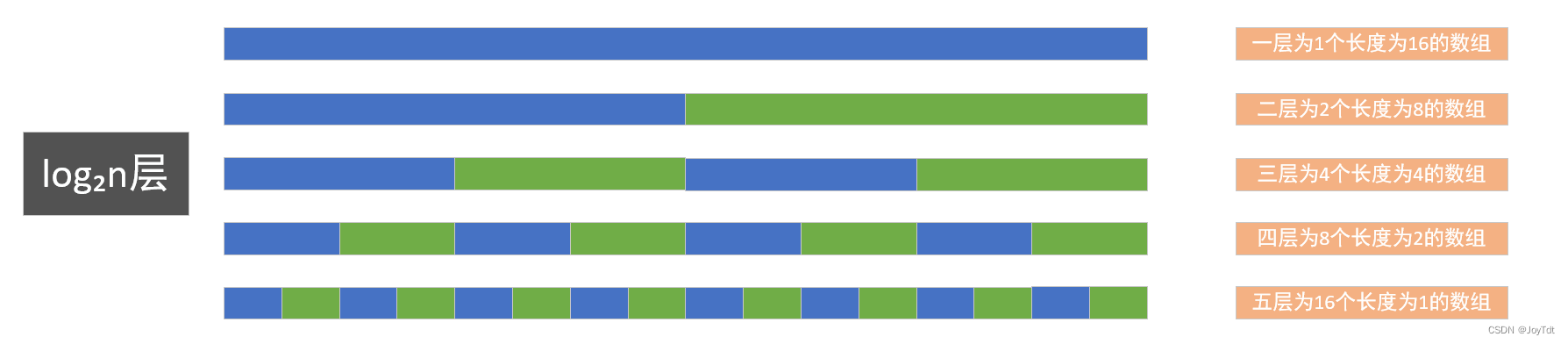
分析：
1.数组长度是n
2.第二层分成2个n/2的数组—————时间复杂度是2O(n/2)=O(N)
3.第三层分成4个n/4的数组—————时间复杂度是4O(n/4)=O(N)
4.要将n最后分治成n个长度为1的数组，共需要log₂n次。也就是第log₂n层，所以归并的时间复杂度是log₂n层乘以每一层O(n)的复杂度，结果是n*log₂n
核心：这个总体思路是分治，先把问题一分在分，不停的递归调用自身，来降低问体规模，但这会造成问题就是合并对时候会非常费劲！
降低规模-递归调用-合并数据

步骤：
1、确定分界点：mid = (l + r) /2
2、递归排序left和right
3、归并排序，合二为一，将两个有序序列合成一个序列，放在新数组temp中
4、复制temp数组到对应原数组的对应位置

模板：

void mergesort(int* q, int l, int r) //归并排序
{
   
   
	if (l >= r) return; 
    int mid = (l + r) >> 1;

    mergesort(q, l, mid);
    mergesort(q, mid + 1, r);
    // 到此已经排好mid左边和右边各自内部的顺序了

    int k = 0, i = l, j = mid + 1;
    int* temp = new int[r - l + 1];
    while (i <= mid && j <= r)
    {
   
   
        if(q[i] <= q[j]) temp[k++] = q[i++];
        else temp[k++] = q[j++];
    }
    while (i <= mid) temp[k++] = q[i++];
    while (j <= r) temp[k++] = q[j++];
    for (i = l, j = 0; i <= r; i++, j++) q[i] = temp[j];
}

二、二分

在数组中查找x的索引位置(前提有序)：
1、将要查找值x与数组中间值mid相比较；
2、如果x=mid，则找到x，退出程序；
3、如果x<mid，则将边界设为[left,mid]；
4、如果x>mid，则将边界设为[mid+1,right]；
5、循环执行3，4两步骤，若直到数组长度为1，还没找到x，则数组中不存在x。如果找到x，则l就是x的位置；
* 注意每次二分会把答案区间缩小一半，且区间里一定有答案

需要注意if
check(mid)为true时，如果正确答案在mid的右侧，即要使l = mid，此时上面mid的取值为mid = (l + r + 1) >> 1；
check(mid)为true时，如果正确答案在mid的左侧，即要使r = mid，此时上面mid的取值为mid = (l + r) >> 1；

（一）整数二分算法

选择答案所在区域，确定使用哪个模板；其实目的就是寻找满足check条件的边界值x的索引位置
时时刻刻要保证答案(x的索引位置)在区间内,当这个区间长度为1时，则认为找到了答案
模板：

bool check(int x) {
   
   /* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
   
   
    while (l < r)
    {
   
   
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：注意l = mid和r = mid - 1时候对应mid = l + r + 1
int bsearch_2(int l, int r)
{
   
   
    while (l < r)
    {
   
   
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

例子：

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int n, m;
int q[];

int main()
{
   
   
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
   
   
        scanf("%d", &q[i]);
    }
    
    while(m--)
    {
   
   
        int x;
        scanf("%d", &x);

        int l = 0, r = n - 1;
        //找符合条件的左边界l
        while(l < r)
        {
   
   
            int mid =