[LeetCode] 数组完整版 — 循环不变量原则 | 双指针法 | 滑动窗口 | 前缀和

基本概念

数组是存放在连续内存空间上的相同类型数据的集合

数组的元素是不能删除，只能覆盖

因为数组在内存空间的地址是连续的，所以在删除或者增添元素的时候，就难免要移动其他元素的地址

在C++中二维数组也是连续分布的

循环不变量原则

循环不变量原则：在循环内保持不变量（如区间的定义），在循环中坚持根据查找不变量来做处理

704# 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

前提：数组为有序数组，数组中无重复元素（即结果唯一）

循环不变量原则：在二分查找的过程中，保持不变量（区间的定义），在循环中坚持根据查找区间的定义来做边界处理

定义查找的范围 [left,right]，初始查找范围是整个数组。每次取查找范围的中点 mid，比较 nums[mid] 和 target 的大小，如果相等则 mid 即为要寻找的下标，如果不相等则根据 nums[mid] 和 target 的大小关系将查找范围缩小一半

注意：while(left < right) or while(left <= right)，right = middle or right = middle - 1 与区间开闭相关

tips：

(right - left) >> 1 等同于 (right - left) / 2

由于每次查找都会将查找范围缩小一半，因此二分查找的时间复杂度是 O(log n)，其中 n 是数组的长度

// O(log n) 0ms; O(1) 30.71MB
class Solution {
   
public:
    int search(vector<int>& nums, int target) {
   
        int left = 0, right = nums.size() - 1;
        while(left <= right) {
   
            int mid = left + (right - left) / 2;
            int num = nums[mid];
            if (target == num) {
   
                return mid;
            } else if (target < num) {
   
                right = mid - 1;
            } else {
   
                left = mid + 1;
            }
        }
        return -1;
    }
};

59# 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

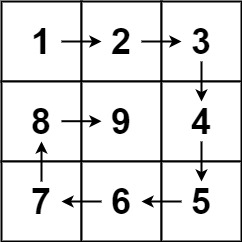
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

每一圈画四条边，每条边都坚持左闭右开

每一圈起始点(x+1, y+1)，边界-1

n分为奇偶数模拟发现偶数刚好，而奇数需要添加中间值

// O(n^2) 0ms; O(1) 9.39MB
class Solution {
   
public:
    vector<vector<int>> generateMatrix(int n) {
   
        vector<vector<int>> matrix(n, vector<int>(n, 0));
        int start_x = 0, start_y = 0;
        int end_x = n - 1, end_y = n - 1;
        int count = 1;

        int loop = n / 2;
        
        while(loop--){
   
            for(int j = start_y; j < end_y; j++) matrix[start_x][j] = count++;

            for(int i = start_x; i < end_x; i++) matrix[i][end_y] = count++;

            for(