AcWing算法基础课笔记1（持续更新）

算法基础课

😄AcWing算法基础课链接

🐵 写题解的浏览器插件：acwing-helper (greasyfork.org)

目录：

一级标题 哪一讲

​ **二级标题 **题目，知识点（两个数字）

​ **三级标题 **小节 （三个数字）

​ 四级标题 小节内容

每个小节对应一道题，小节标题下附上题目链接和题解代码，小节内容中写下分析过程、证明过程，时间复杂度分析、思维模式等笔记，或写下一些启发。

第一讲 基础算法

• 输入输出处理方法

C++ 中，数据量大用scanf速度更快，数据量小用cin

C++也可以使用cin.tie(0);和ios::sync_with_stdio(false);来提高cin的速度。副作用就是整段代码都无法使用scanf了

java 输入用buffer reader ，比scan 快十几倍

• 数组初始化：默认数组中的值为0
• 数组访问：C++没有内置的数组边界检查，如果访问超出数组边界的内存空间，是一种不安全的行为。

• 模版总结：常用代码模板1——基础算法 - AcWing

  模版要在理解的前提下背熟，考试就是比拼的记忆力和毅力（自制力）！

1.1 快速排序

1.1.1 快速排序

785. 快速排序 - AcWing题库

#include <iostream>

using namespace std;

const int N = 100010;

int q[N];

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];	// 左边界，下面不能取再递归i
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }

    quick_sort(q, l, j);	// 递归右边界j
    quick_sort(q, j + 1, r);
}

int main()
{
    int n;
    scanf("%d", &n);

    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    quick_sort(q, 0, n - 1);

    for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);

    return 0;
}

边界问题

• 若下面递归的两个区间是[l , j] 和 [j + 1 , r]， x（枢轴元素）不能取a[r]（右边界），因为j是右边界

// 右边界
int x = a[(l + r + 1) / 2];
int x = a[l + (r - l) + 1 / 2 ];

// 对应
quick_sort(q, l, i - 1);
quick_sort(q, i, r);

• 若下面递归的两个区间是[l , i - 1] 和 [i , r] ， x（枢轴元素）不能取a[l]（左边界），因为i是左边界

// 左边界
int x = a[(l + r) / 2];
int x = a[l + (r - l) / 2 ];

// 对应
quick_sort(q, l, j);
quick_sort(q, j + 1, r);

• 反例：

2 
0 1 

总之：用i，不能取到左边界；用j，不能取到右边界。

时间复杂度

递归每层时间复杂度为n

共$lo{g}_{2}n$层（使用树的高度来证明）

最坏时间复杂度为$O(n^2)$

Tips

防止右值过大导致溢出

int x = a[l + (r - l) / 2 ];   //---> 有可能取到l（左边界）

快排是不稳定的，快排如何变稳定？

让快排里面所有数都不同，<a , i> 用二元组形式。

C++不能返回数组

// C++不能返回数组，只能返回指针，（定长）数组要在函数外面定义好了，再传进函数。
// return a[];

1.1.2 快速查找（基于快排）

786. 第k个数 - AcWing题库

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n , k;
int a[N];

int quick_search(int l , int r , int k)
{
    if(l == r) return a[l];
    
    int i = l - 1 , j = r + 1;
    int x = a[i + (j - i + 1) / 2];
    while(i < j)
    {
        do i++ ; while(a[i] < x);
        do j-- ; while(a[j] > x);
        if(i < j) swap(a[i] , a[j]);
    }
    if(k <= i - 1) return quick_search(l , i - 1 , k);	// 判断要找的数属于哪一个区间，递归查找哪一个区间即可
    return quick_search(i , r , k);
}

int main()
{
    scanf("%d%d" , &n , &k);
    for(int i = 0 ; i<n ; i++) cin >> a[i]; 
    
    cout << quick_search(0 , n - 1 , k - 1) << endl;
    return 0;
}

时间复杂度

2n --> $O(n)$（因为相比快排剪枝了），证明如下图：

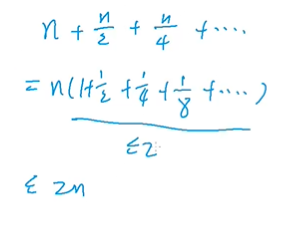
第一层需要处理区间大小为n，第二层需要处理的为n/2，第三层为n/4，以此类推

每次处理的区间大小都为一半。

1.2 归并排序

1.2.1 归并排序

787. 归并排序 - AcWing题库

#include <iostream>

using namespace std;

const int N = 10 + 10e6;
int n; 
int q[N] , tmp[N];

void merge_sort(int q[] , int l , int r)
{
    if(l >= r) return;
    
    int mid = l + r >> 1;
    merge_sort(q , l ,mid);
    merge_sort(q , mid + 1 , r);
    
    int i = l , j = mid + 1 , k = 0;
    while (i <= mid && j <= r)
    {
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }
    
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    
    for (int i = l , j = 0 ; i <= r ; i ++ ,j ++) q[i] = tmp[j];
}

int main()
{
    scanf("%d" , &n);
    for (int i = 0; i < n; i ++ ) scanf("%d" , &q[i]);
    
    merge_sort(q , 0 , n - 1);
    
    for (int i = 0; i < n; i ++ ) printf("%d " , q[i]);
    
    return 0;
}

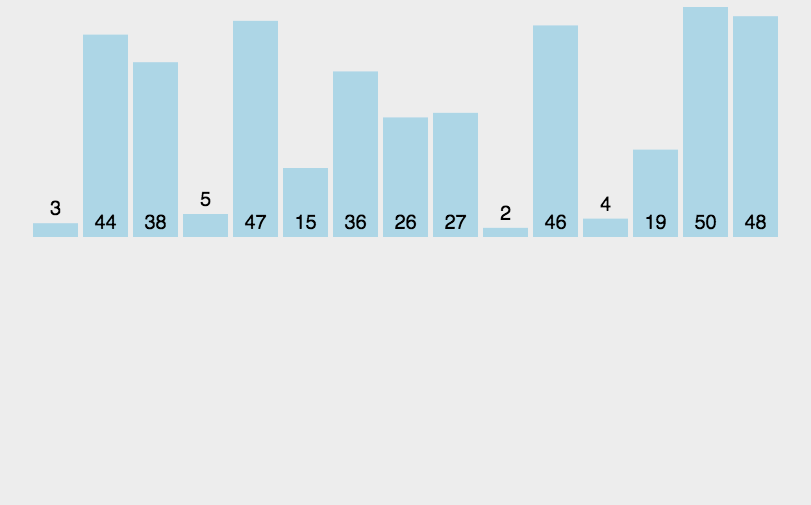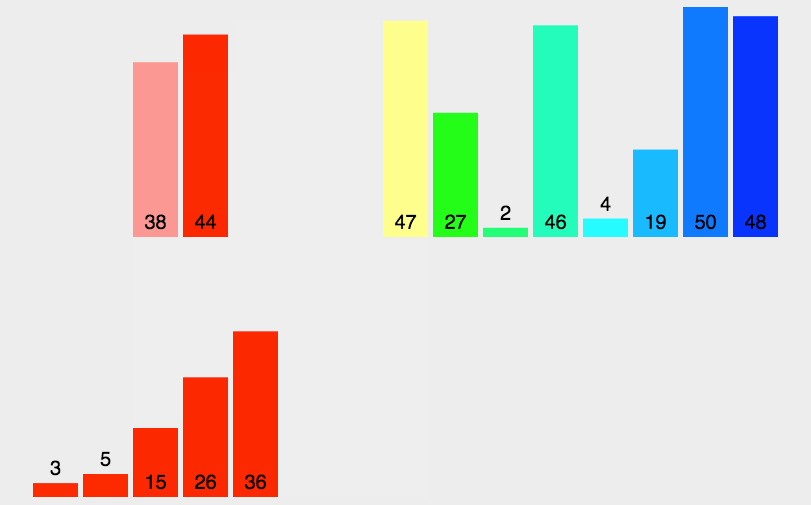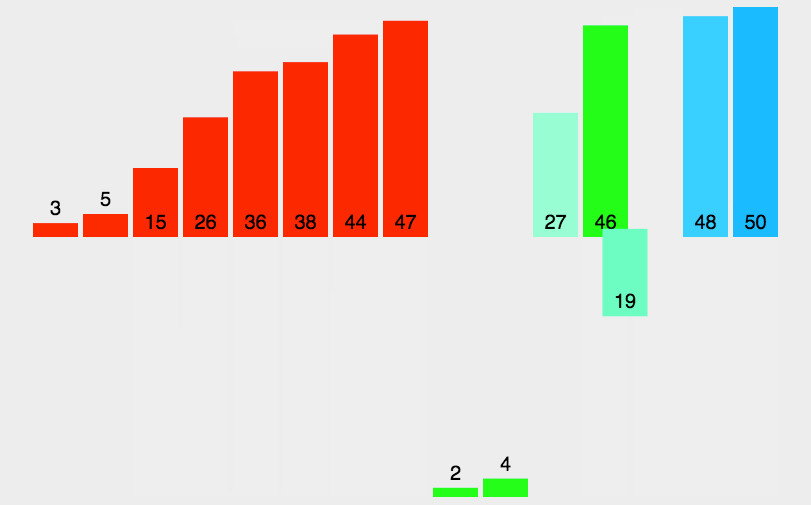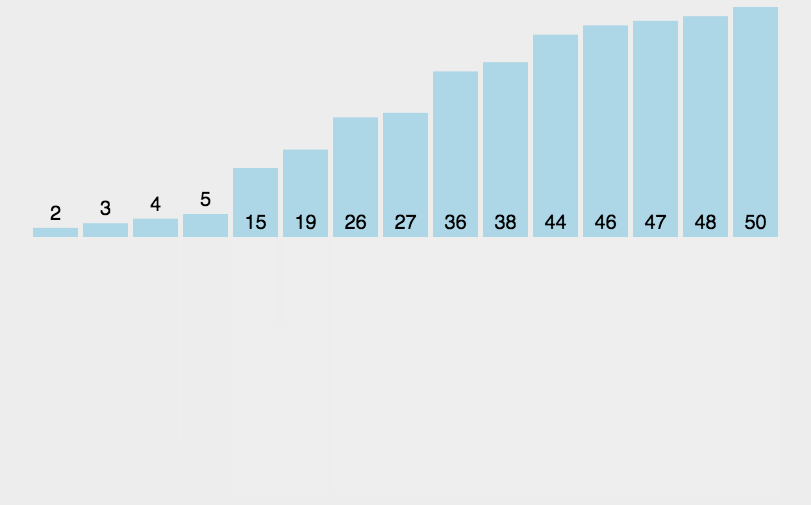
归并排序,它有两大核心操作.

一个是将数组一分为二,一个无序的数组成为两个数组.

另外一个操作就是,合二为一,将两个有序数组合并成为一个有序数组.

时间复杂度

$O(nlogn)$ 每层排序的时间复杂度是n，共logn层

类似于快排，只不过快排是排完再分区间（递归），归并是先分完（递归）再排。

Tips

归并排序是稳定的

1.2.2 在归并排序中处理逆序数量

788. 逆序对的数量 - AcWing题库

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;
int n;
int a[N] , tmp[N];

LL merge_sort(int l , int r){
    if(l >= r) return 0;
    
    int mid = l + r >> 1;
    // res不能定义为int ，可能会超出范围，考虑极端情况 n + n-1 + n-2 + n-3 + ...... = n(n - 1) / 2 
    // 数据是十万，代入约为 5 x 1e9 超出int范围
    LL res = merge_sort(l , mid) + merge_sort(mid + 1 , r);
    
    int k = 0 , i = l , j = mid + 1;  // 区间[i , mid] , [j , r]
    while(i <= mid && j <= r)
    {
        if(a[i] <= a[j]) tmp[k++] = a[i++];
        else
        {
            tmp[k++] = a[j++];
            res += mid - i + 1;
        }
    }
    while(i <= mid) tmp[k++] = a[i++];
    while(j <= r) tmp[k++] = a[j++];
    
    // 还是不能省tmp这个空间，因为要更新原数组，后面的递归才得以更新，不重复工作
    for(i = l , j = 0; i <= r ; i++ , j++) a[i] = tmp[j];
    
    return res;
}

int main()
{
    scanf("%d" , &n);
    for(int i = 0 ; i < n ; i++ ) scanf("%d" , &a[i]);
    
    cout << merge_sort(0 , n - 1) << endl;
    return 0;
}

思路：

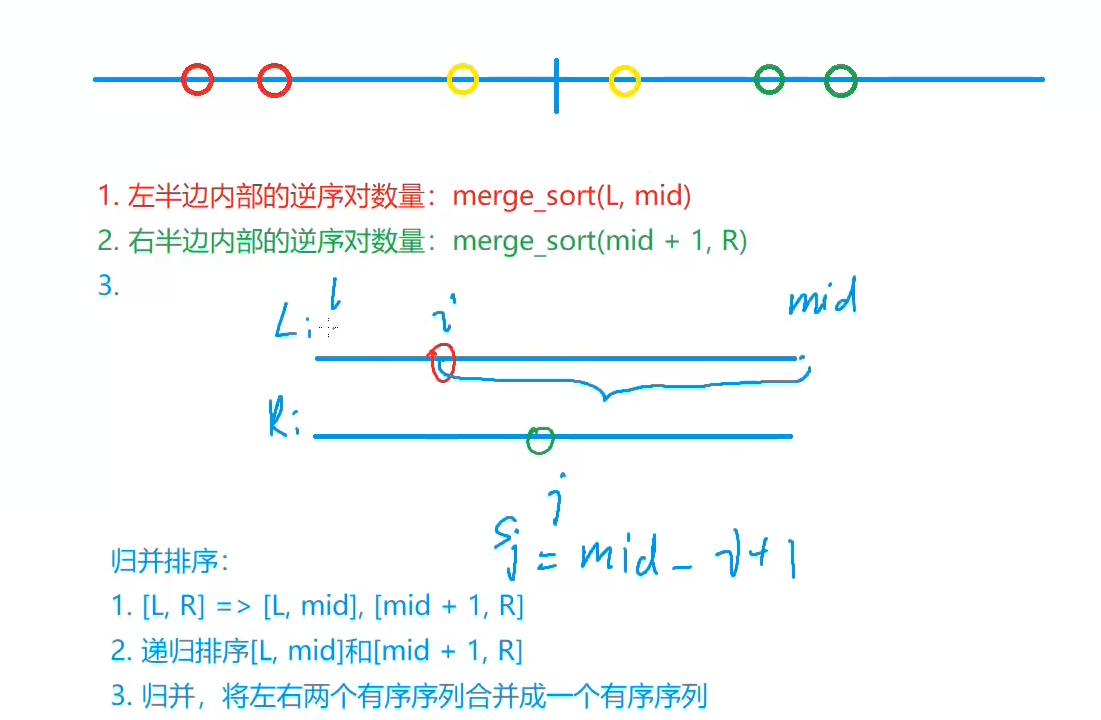
假定有把一个无序序列一分为二为两个有序序列，然后对其归并，设置双指针 i ， j 分别指向左半区间和右半区间，即两个元素 a 和 b 分别位于左右两个区间产生的逆序对数量为 s0，元素 a 和 b 同时位于左半区间或右半区间产生的逆序对数量为s1和 s2。

那么，当指针 i 所指的元素 nums[i] 第一次大于指针 j 所指的元素 nums[j] 时，从此时起区间 [i,mid] 里的所有元素都一定大于指针 j 所指的元素 nums[j] ，区间长度 mid−i+1 （图中大括号所标示的区间）就是左半区间对指针 j 所指的元素 nums[j] 的逆序对数量，把所有单个元素的逆序对数量累加，就得到了该序列的逆序对数量s0。

由于序列左右半边的逆序对数量s1,s2可以递归求出，因此该序列的逆序对总数量为 s=s0+s1+s2。

因为每一趟归并排序（都是两个有序的序列合并）都可以求出当前序列的逆序对数量，所以归并排序可以用来求解整个序列逆序对数量。

• ⭐️ 归并的本质

递归到最后区间都是由一个数组成，然后再逐个合并，所有我认为只会出现第3中情况，即一个在左，一个在右

其实本质还是递归跟分治。
假设给你两个有序列的数组A,B,求那么显然，A和B的逆序数就都是0对不对，所以将A,B按照顺序接成一个新的数组的逆序数，是不是就等于求y总视频中所讲的黄色逆序数的个数？
本质就是 C由A,B构成，那么对C求某些特定的性质，可以等价于 对A求(红色）加上对B求（绿色），再加上将A，B整合之后产生的性质（黄色），然后又可以将A看作由更小的 E，F。而但数组不可以再划分的时候，即只要一个元素的时候，就是我们递归的尽头了。
所以归并的本质还是求黄色的逆序数，因为A红色的逆序数可以等于A的红色+黄色+绿色，而最底层的红色和绿色都为0，所以本质是求黄色。

• 为什么用归并排序可以边排序边计算？

因为算完排好序可以避免重复统计逆序数对，而且可以减少对比次数，降低时间复杂度。

我们注意到一个很重要的性质，左右半边的元素在各自任意调换顺序，是不影响第三步计数的，因此我们可以数完就给它排序。这么做的好处在于，如果序列是有序的，会让第三步计数很容易。
如果无序暴力数的话这一步是O(n^2)的。

比如序列是这样的

4 5 6 | 1 2 3
当你发现 4 比 3 大的时候，也就是说右边最大的元素都小于左边最小的元素，那么左边剩下的5和6都必然比右边的所有元素大，因此就可以不用数5和6的情形了，直接分别加上右半边的元素个数就可以了，这一步就降低到了O(n), 我们知道递归式 T(n) = 2T(n/2)+O(n) = O(nlogn)的，所以排序的成本是可以接受的，并且这一问题下，可以很自然地使用归并排序。

Tips

局部思考，适用于分治、递归类型算法

假设两个已经排好序的序列，思考如何求逆序。

更一般来说，只考虑每一个小递归区间对问题的处理方法。

因为类似于这种分治的算法，是递归的，在每一个小的区间上处理、解决问题，然后就可以递归到处理整个区间。

算法的特性、背后的思想决定了算法能解决什么题目

提问：

归并算法模板是用来解决哪一类的问题的？
换句话说就是，归并算法的运作本质是什么？为什么求逆序对的数量我会想到归并算法而不是其他算法？
归并算法和其他算法的区别在哪里？我觉得这才是我们应该关注的问题，否则遇到一个新的题目的话，我们明明会写归并算法，但是却不知道我们可以用归并算法来解决，学这个归并算法我觉得不能只会写模板或者只会求逆序对，然后换汤不换药来考结果还是不会，如果能搞清楚归并算法本质，这样下次我遇到类似的题目，分析之后我就能想起来用归并算法，知道归并算法能解决这一类的问题，我觉得才是把归并算法学明白了

回答：

(见上方⭐️归并的本质 )

归并排序的本质是分治，分治是一种思想，可以用分治的解决的问题可以尝试使用基于分治思想的算法来解决。

比如这道题，利用归并排序的局部有序来分治统计逆序对数量，而快排在递归的过程中只能保证局部中前面的数小于等于某个数，后面的数大于等于某个数，由于存在等于的情况，需要特殊处理，相较于归并排序步骤会多一些。归并只有将结果求出来后才能得到第i小的数，快排可以平均上省去一半时间，这是算法特性。

❓ 解决多维偏序问题，可以用归并思想（CDQ分治），降掉一个维度。
逆序对就是典型的二维偏序问题。

1.3 二分

1.3.1 整数二分

789. 数的范围 - AcWing题库

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n , q;
int a[N];

int findLeftBound(int l , int r , int x)	// 找左边界，右边的那个数
{
    while(l < r)
    {
        int mid = l + (r - l) / 2;
        if(a[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;		// 输出l 或 r 都一样，因为while结束时，l = r
}

int findRightBound(int l , int r , int x)	// 找右边界，最左边的那个数
{
    while(l < r)
    {
        int mid = l + (r - l + 1) / 2;
        if(a[mid] <= x) l = mid;
        else r = mid - 1;
    }
    return l;
}

int main()
{
    scanf("%d%d" , &n , & q);
    for(int i = 0 ; i < n ; i++) scanf("%d" , &a[i]);
    while(q--)
    {
        int k ;
        scanf("%d" , &k);
        
        int begin = findLeftBound(0 , n - 1 , k);
        if(a[begin] != k) cout << "-1 -1" << endl;
        else cout << begin << " " << findRightBound(begin , n - 1 , k) << endl;
    }
    return 0;
}

[注]：如果无解，模版1二分出来的是区间内从左到右第一个满足 $check()$ 的元素。

在本题中，就是右半区间左边第一个 >= x 的数。

二分的本质

单调 $\Rightarrow$可二分,单调$\nLeftarrow$可二分

二分的本质并不是单调性，满足单调性的数组一定可以使用二分查找，但可以使用二分查找的数组不一定需要满足单调性

单调性不是二分的本质，太过于狭隘。

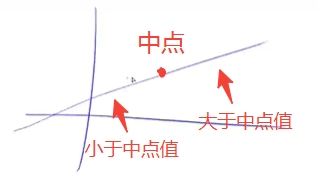
二分的本质是找到一个性质，该性质使得整个区间被一分为二（左半边满足，右半边不满足），如下图

整个区间被分为了红色部分和绿色部分，两个模版分别找的就是红色的边界和绿色的边界（图中两个箭头$\downarrow$处）。

找满足条件区间的边界

1. ⬅️ 在满足 $check()$ 的区间找左边界点取 $mid = (l + r) / 2 $

   此处 $check(mid)$ 函数用于判断 $mid$ 是否满足绿色区间：

• 若是，说明要找的左（红色）区间边界在区间 $[mid,r]$ 上，更新 $l = mid $ （注意此处更新区间包含$mid$，因为此时$mid$有可能是答案）

• 若不是，说明要找的左（红色）区间边界在区间 $[l,mid-1]$ 上，更新 r = m i d − 1 r=mid-1