lq-递归

原创已于 2023-01-22 10:21:52 修改 · 410 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#java

于 2023-01-17 11:09:18 首次发布

java 专栏收录该内容

81 篇文章

订阅专栏

文章提供了三个使用Java实现的递归算法，分别是用于生成1到n所有选择方案的指数型枚举，随机打乱1到n顺序的排列型枚举，以及计算斐波那契数列前N项的算法。每个算法都详细展示了递归搜索树和AC代码实现。

1、递归实现指数型枚举

从 1∼n 这 n个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 n。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

1 ≤ n ≤ 15

输入样例：

输出样例：

递归搜索树：

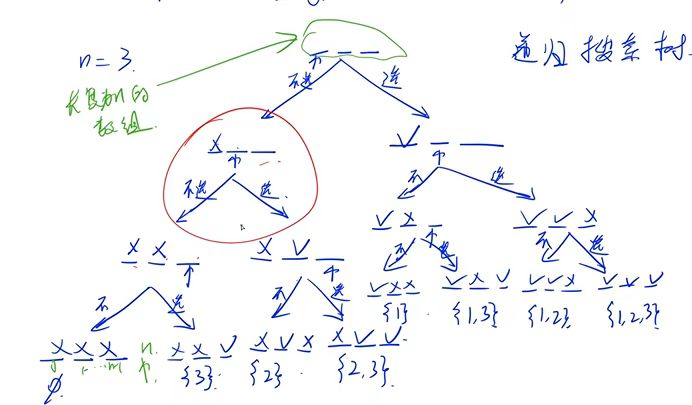
AC代码：

package 做题;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main 
{
    static final int N = 16;
    static BufferedWriter wr;
    static int st[] = new int[N];
    
    static int n;
    
    public static void dfs(int u) throws Exception  //第几层就是筛选第几个数字
    {
        if(u > n) //不可以有等号，如果有等号会少一层递归，即最后一层无法递归 
        {
            for(int i = 1 ; i <= n ; i ++) // 从1到n选择
            {
                if(st[i] == 1)  wr.write(i+" ");// 把选的数打印出来
            }
            wr.write("\n");
            return;
        }
        
        // 不选这个数字
        st[u] = 2;
        dfs(u + 1);
        st[u] = 0;
        
        // 选这个数字
        st[u] = 1;
        dfs(u + 1);
        st[u] = 0;
    }
    
    public static void main(String[] args) throws Exception, IOException 
    {
        BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
        wr= new BufferedWriter(new OutputStreamWriter(System.out));
        n = Integer.parseInt(rd.readLine().trim());
        dfs(1);
        wr.flush();
        wr.close();
        rd.close();
    }
}

2、递归实现排列型枚举

把 1∼n 这 n个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数 n。

输出格式

按照从小到大的顺序输出所有方案，每行 1个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围

1≤n≤9

输入样例：

输出样例：

递归搜索树：

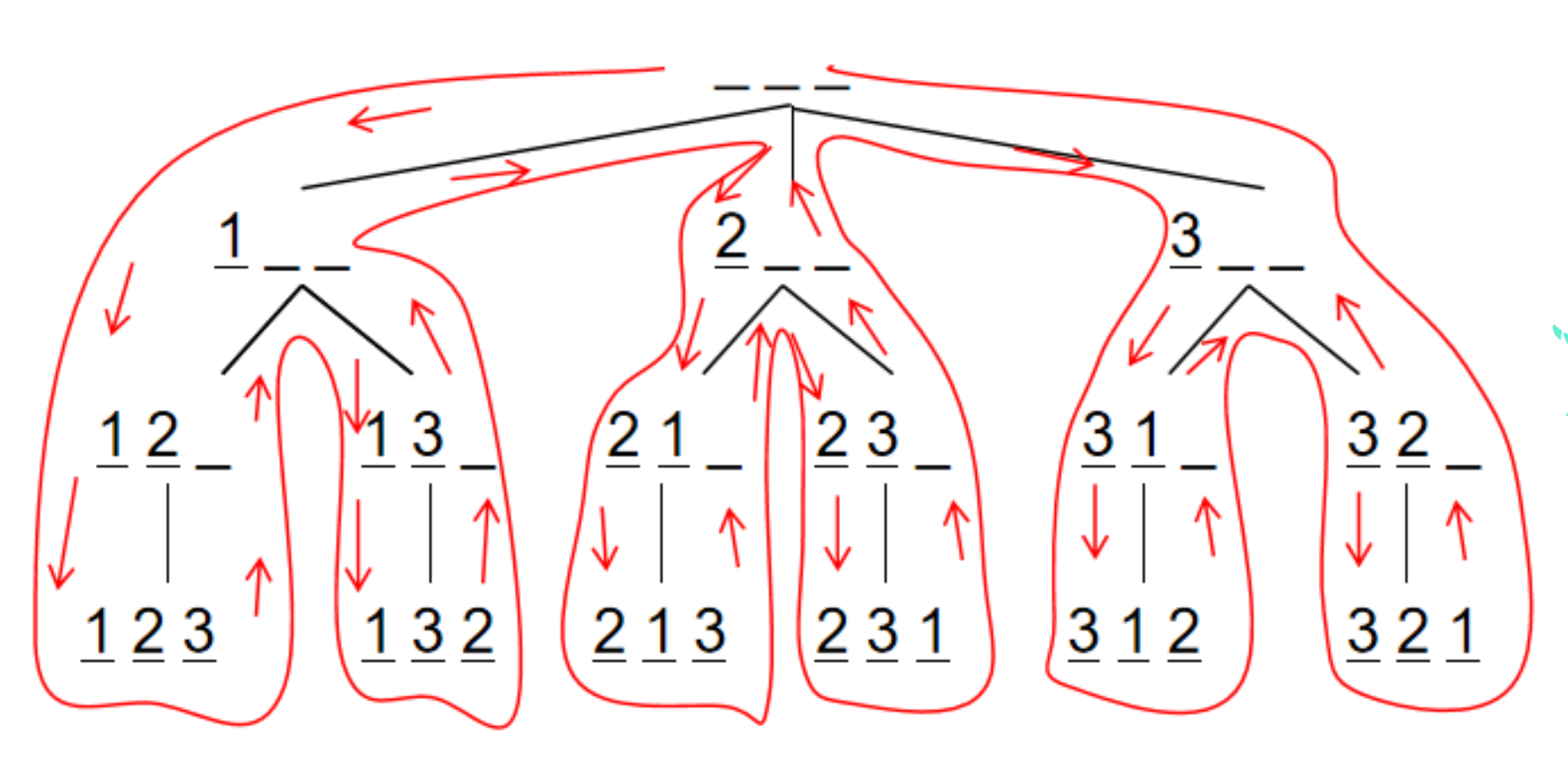
AC代码：

package 做题;
import java.awt.Taskbar.State;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main 
{
    static final int N = 16;
    static BufferedWriter wr;
    static int state[] = new int[N];// 0 表示还没放数，1~n表示放了哪个数
    static boolean used[] = new boolean[N];// true表示用过，false表示还未用过
    
    static int n;
    
    public static void dfs(int u) throws Exception 
    {
        if(u > n) // 边界
        {
            for(int i = 1 ; i <= n ; i ++)  wr.write( state[i] + " "); // 打印某个方案
            wr.write("\n");
            return;
        }
        
        // 依次枚举每个分支，即当前位置可以填哪些数
        for(int i = 1 ; i <= n ; i ++)
        {
            if(!used[i])
            {
                state[u] = i;
                used[i] = true;
                dfs(u + 1);
                
                // 恢复现场
                state[u] = 0;
                used[i] = false;
            }
        }
    }
    
    public static void main(String[] args) throws Exception, IOException 
    {
        BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
        wr= new BufferedWriter(new OutputStreamWriter(System.out));
        n = Integer.parseInt(rd.readLine().trim());
        dfs(1);
        wr.flush();
        wr.close();
        rd.close();
    }
}

3、简单斐波那契

以下数列 0 1 1 2 3 5 8 13 21 ... 被称为斐波纳契数列。这个数列从第 3项开始，每一项都等于前两项之和。输入一个整数 N，请你输出这个序列的前 N项。

输入格式

一个整数 N。

输出格式

在一行中输出斐波那契数列的前 N

项，数字之间用空格隔开。

数据范围

0<N<46

输入样例：

输出样例：

0 1 1 2 3

递归搜索树：

（每个f（x）的最底层到f（0）或者f（1），因为这样才能算出值来）

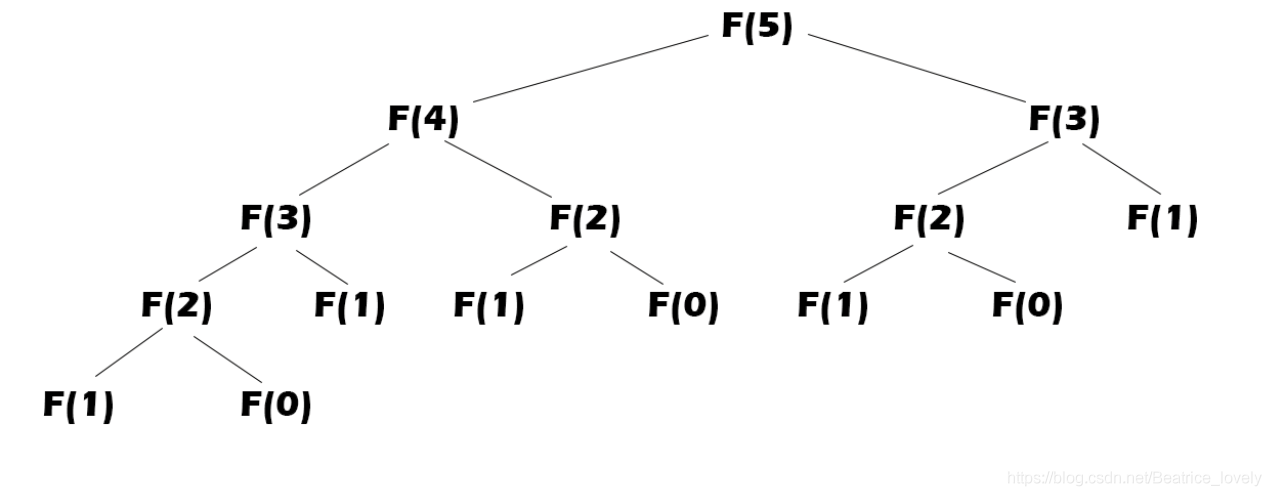
package 做题;
import java.awt.Taskbar.State;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class Main 
{
    static final int N = 50;
    static BufferedWriter wr;
    static int a[] = new int[N];
    
    static int n;
    
    static void dfs(int u) throws Exception 
    {
        if(u == n - 1)  return;  // 因为a[0]和a[1]有初值，一上来就更新了a[2],例如，如果计算f（5）（n等于5）即a[4]（a[4] = a[3]和a[2]在u = 2的时候更新），更新完后，在u = 3的时候return，结束值的更新，确实够用了，但是如果n = 1，n - 2 = -1，u从主函数第一次进去dfs函数的时候等于0，u只递增，不可能是负数，所以会无限递归，直到栈爆，所以位置需要偏移一下，u == n - 1的时候结束递归来应对n == 1，多递归一层更新新的数也无所谓，寄不了
        a[u + 2] = a[u + 1] + a[u];
        dfs(u + 1);
    }
    
    public static void main(String[] args) throws Exception, IOException 
    {
        BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
        wr= new BufferedWriter(new OutputStreamWriter(System.out));
        n = Integer.parseInt(rd.readLine().trim());
        
        a[0] = 0;
        a[1] = 1;
        
        dfs(0);
        
        for(int i = 0 ; i < n ; i ++)  wr.append(a[i] + " ");
        
        wr.flush();
        wr.close();
        rd.close();
    }
}

4、费解的开关

你玩过“拉灯”游戏吗？

25盏灯排成一个 5×5 的方形。

每一个灯都有一个开关，游戏者可以改变它的状态。

每一步，游戏者可以改变某一个灯的状态。

游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。

我们用数字 1表示一盏开着的灯，用数字 0表示关着的灯。

下面这种状态

在改变了最左上角的灯的状态后将变成：

再改变它正中间的灯后状态将变成：

给定一些游戏的初始状态，编写程序判断游戏者是否可能在 6步以内使所有的灯都变亮。

输入格式

第一行输入正整数 n，代表数据中共有 n 个待解决的游戏初始状态。

以下若干行数据分为 n组，每组数据有 5 行，每行 5个字符。

每组数据描述了一个游戏的初始状态。

各组数据间用一个空行分隔。

输出格式

一共输出 n行数据，每行有一个小于等于 6

的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。

对于某一个游戏初始状态，若 6步以内无法使所有灯变亮，则输出 −1。

数据范围

0<n≤500

输入样例：

输出样例：

3
2
-1

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 6;
    static int[] dx ={-1,0,1,0,0};
    static int[] dy ={0,1,0,-1,0};//上下左右中  偏移量
    static char[][] g = new char[N][N];
    static char[][] backup = new char[N][N];

    // 这个操作是把(x, y)以及上下左右的灯都变成相反的颜色
    static void turn (int x, int y)
    {
        for (int i = 0; i < 5; i ++ )
        {
            int a = x + dx[i], b = y + dy[i];

            //如果在边界外边，直接忽略即可
            if (a < 0 || a >= 5 || b < 0 || b >= 5) continue;
            
            g[a][b] ^= 1;   //异或，不同的时候就变成相反的数
            //【‘0’ ASCII值48 ‘1’ 49】
        }

    }

    public static void main(String[] args) throws Exception, IOException
    {
        BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter wr = new BufferedWriter(new OutputStreamWriter(System.out));
        
        Scanner in = new Scanner(System.in);
        int n = Integer.parseInt(rd.readLine());

        while(n-- >0) 
        {
            // 按行输入，把每一行当成一个字符串 然后转换成字符数组
            for(int i=0;i<5;i++) g[i] = rd.readLine().toCharArray();

            int res = 7;

            //第一行覆盖所有状态
            for(int op=0;op<32;op++)
            {
            // 我在对这种情况操作的时候，得先备用一下
            // 把原始数组备份一下，然后操作g，操作完了还原，然后再操作
                for(int j=0;j<5;++j)
                {
                    backup[j]=Arrays.copyOf(g[j], 5);
                }

                int step = 0;
                //计算翻转操作的step
                for (int i = 0; i < 5; ++i)
                {
                    if ((op>>i & 1) == 1)
                    {
                        step++;
                        turn(0,i);
                    }
                }

                //然后通过第一行按完之后的状态，按234行  递推
                for (int i = 0; i < 4; ++i)
                    for (int j = 0; j < 5; ++j)
                    {
                        if (g[i][j] == '0')
                        {
                            step++;
                            // 如果这个位置是灭的，就按下一行对应的位置
                            turn(i+1,j);
                        }
                    }

                boolean dark  = false;

                for (int j = 0; j < 5; j ++ )
                        if (g[4][j] == '0')
                        {
                            dark = true;
                            break;
                        }

                // 判断可行性 可行的话 是否更优
                if (!dark) res = Math.min(res, step);

                for(int j=0;j<5;++j)
                {
                    g[j]=Arrays.copyOf(backup[j], 5);
                }

             }

            if(res > 6) res = -1;
            System.out.println(res);    
        }
        wr.flush();
    }
}