85.旋转数组

一、题目描述

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

进阶：

尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

二、解题思路

2.1 方案一：使用额外数组

以示例一为例，申请一个新的数组，用于存储旋转之后的数组，遍历每一个元素：

第一步：遍历第一个元素1，应该放在第四个位置上（索引为3），某一个元素应该移动到哪一个索引的位置呢？可以根据计算公式(i+k)%n：

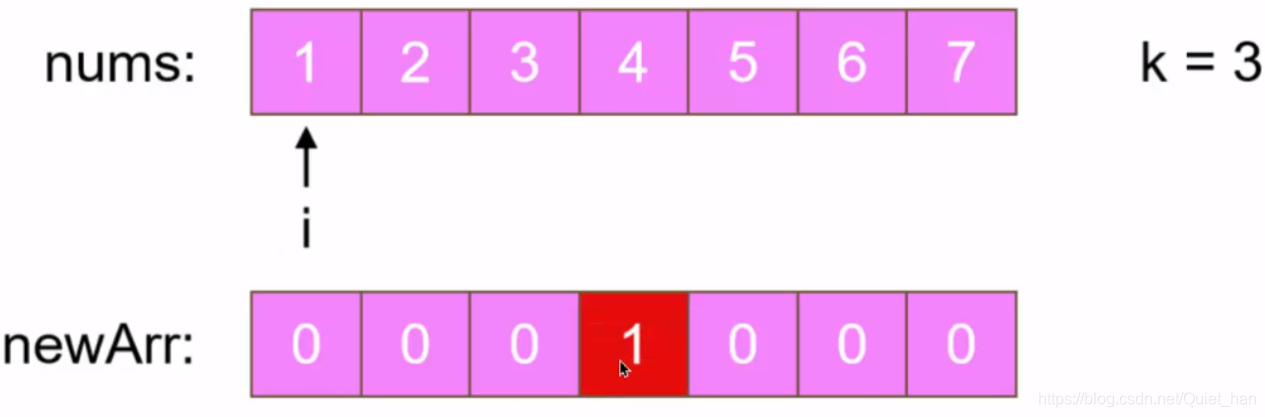
第二步：移动第二个元素2，根据公式(i+k)%n可得该元素应该移动到索引为4的位置上：

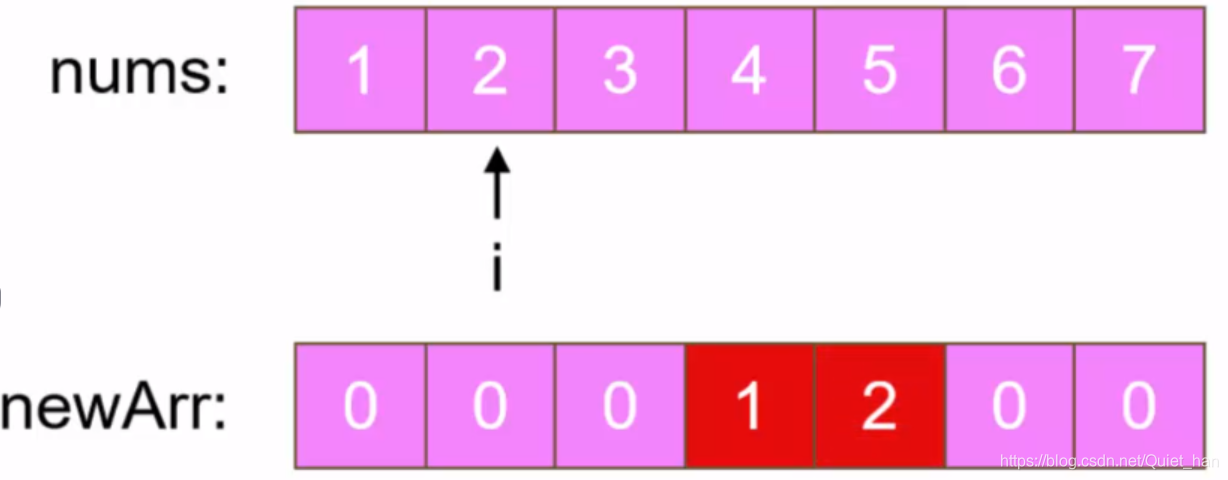
以此类推，根据公式计算每个元素应该移动的位置，最终得到：

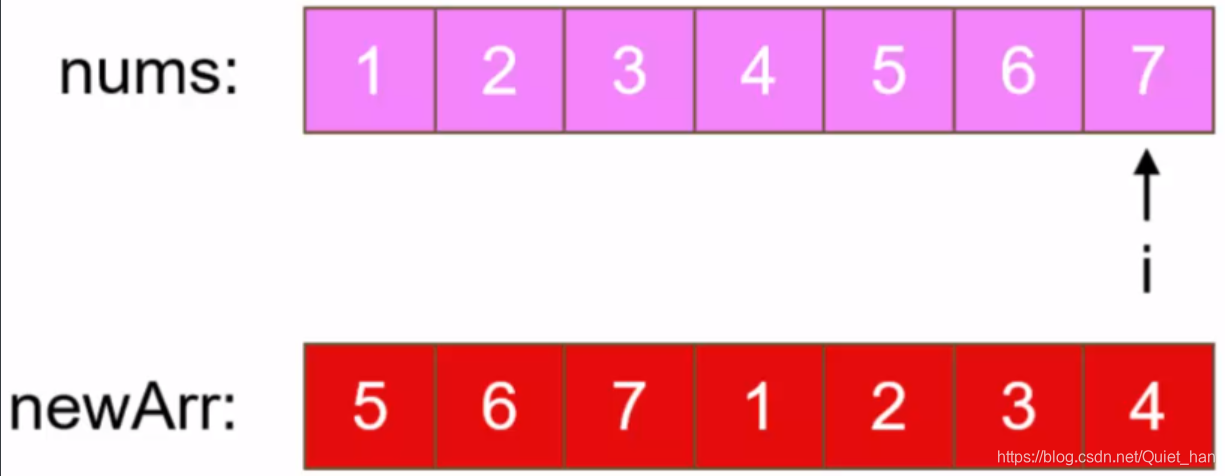
这时，还需要将旋转之后的数组newArr赋值给nums即可。

空间复杂度：因为使用了额外数组，所以为O(n)

2.2 方案二：环状替换

可不可以不适用额外数组呢？在方案一种，计算出某个元素移动之后的index后，在额外数组中将这个值赋值给对应的index位置即可，如果不使用额外数组的话，计算出的index在原数组中的位置是有值的，还是举例来说明：

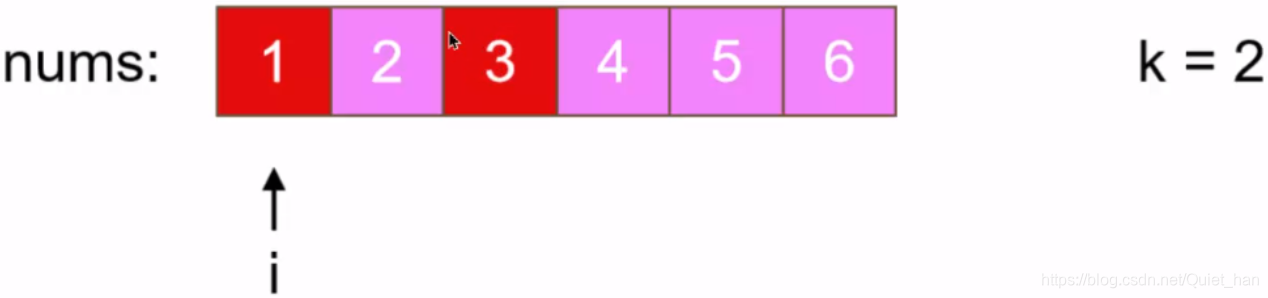
上图，对于第一个元素1，当k等于2的时候，根据公式(i+k)%n可得移动之后的索引位置应该是2，但是如果移动过去的话会覆盖该索引原来的元素3，此时我们可以使用一个变量prev来存储该索引原来的值3，再将1移动过去：

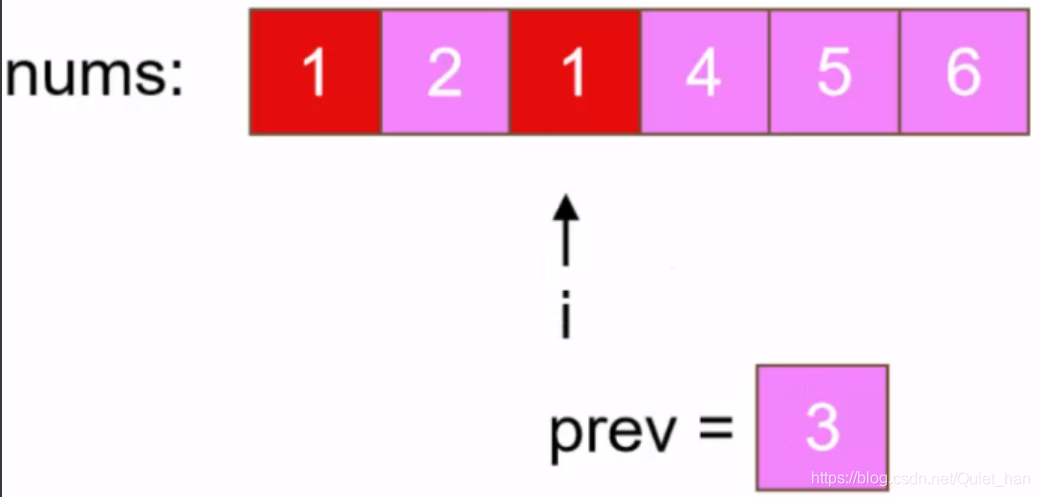
第二步：处理索引为2的这个元素，这个位置上的元素原来的值已经通过变量prev记住了为3，通过公式(i+k)%n得到这个3应该移动到索引为4的位置上，但是索引为4的位置已经有元素了，此时将变量prev存储的值和该索引对应的值进行替换就可以了：

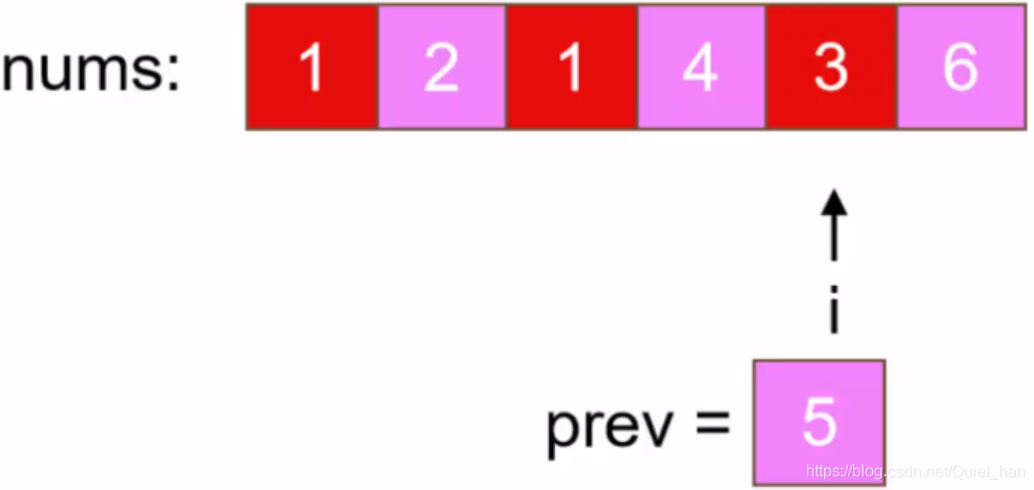
第三步：处理索引为4位置上的值，通过公式计算出该位置的值应该移动到索引为0的位置上，索引为0的元素已经在正确的位置上了，所以直接交换过去即可。

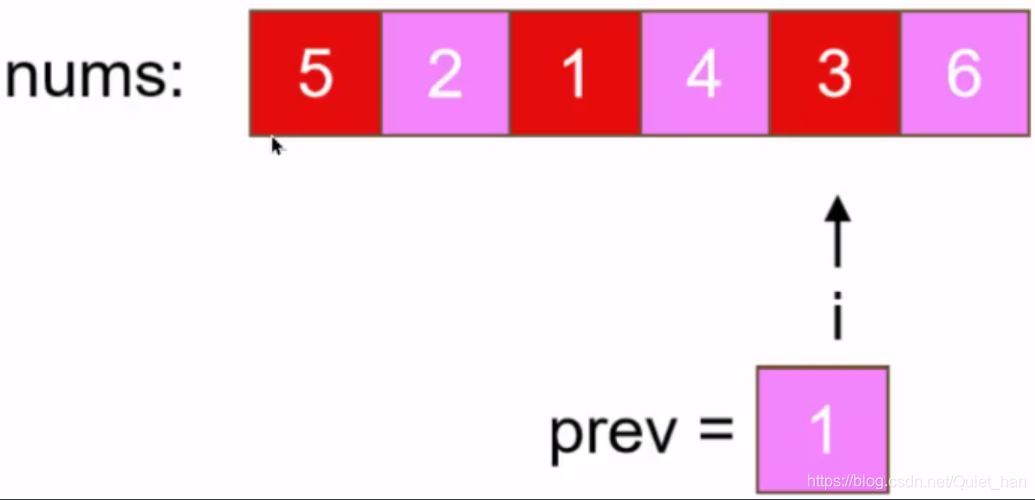
第四步：本来这一步应该处理索引为0的元素，但是这个位置上的值已经处理过了，所以，指针向后移动处理没有处理过的元素2，通过公式，该元素应该移动到索引为3的位置上，该位置上的值还是用prev这个变量来存储，移动之后2就到了正确的位置了：

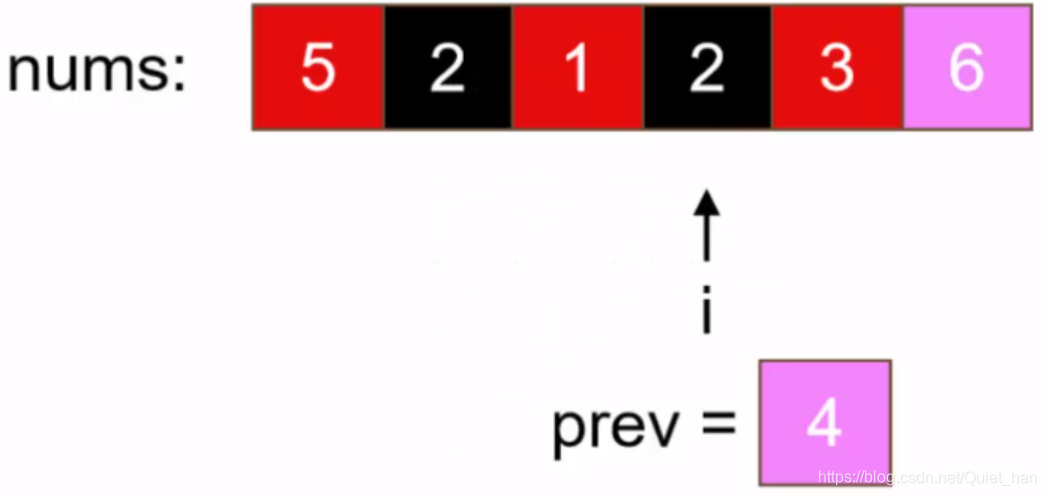
第五步：处理索引为3位置上的值，该位置上的值已经存储到变量prev中了，改值根据公式(i+k)%n应该移动到索引为5的位置上，而索引为5原来的值继续用变量存储：

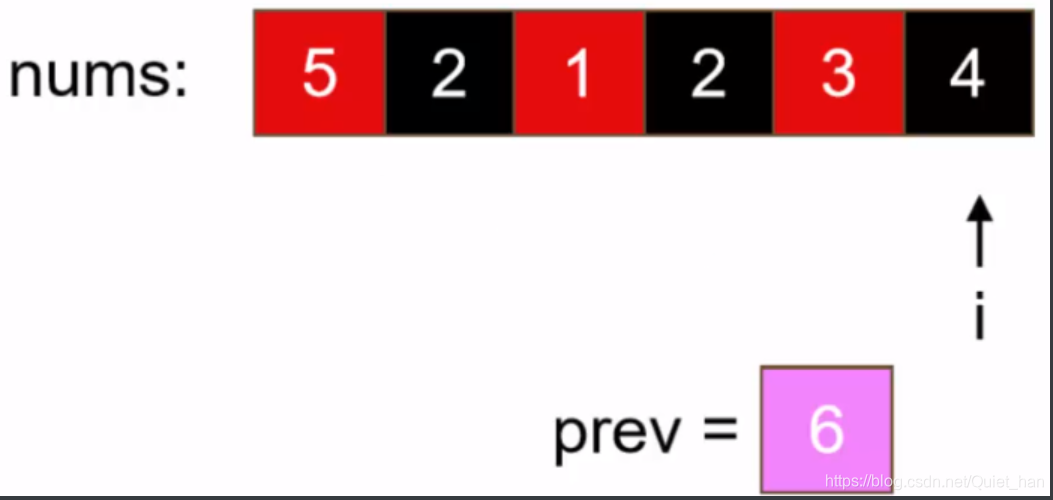
第六步：最后处理索引为5原先的元素，该元素已经用prev存储起来了，根据公式，该位置的元素应该移动到索引为1的位置，最后处理完左右元素，如下：

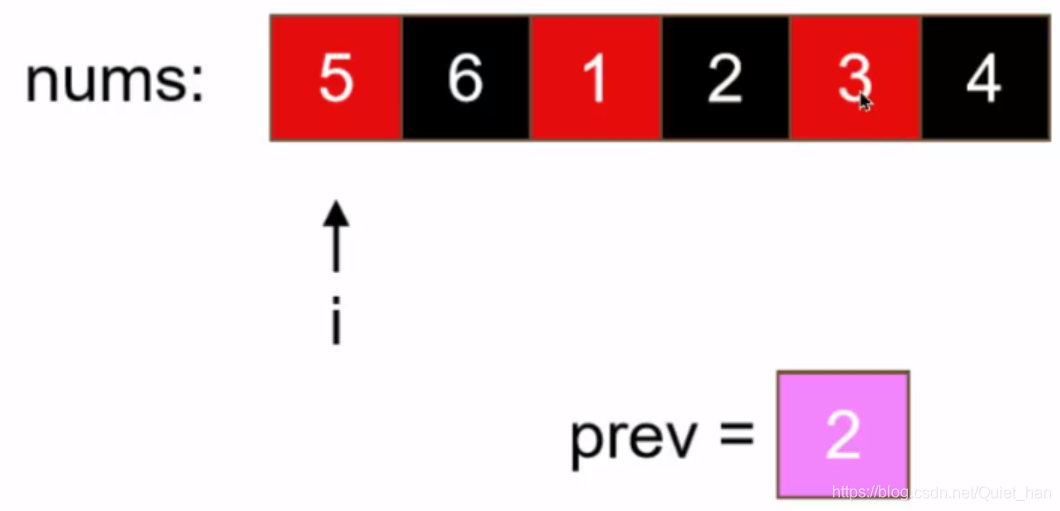
通过上面的步骤不会发现元素的位置替换正好形成一个环状：

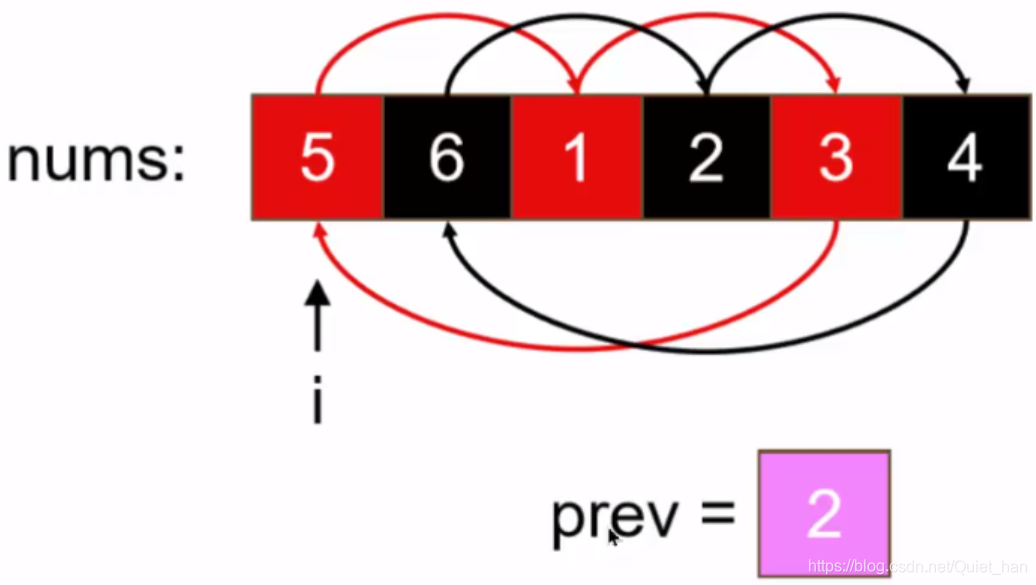
该方法的时间复杂度是O(n)，因为只对数组处理了一遍，空间复杂度是O(1)。

代码实现：

这里需要3个指针一个变量，curr指针用来存储当前元素的索引，start指针是用来循环数组的，next指针是某个元素移动之后的位置索引：

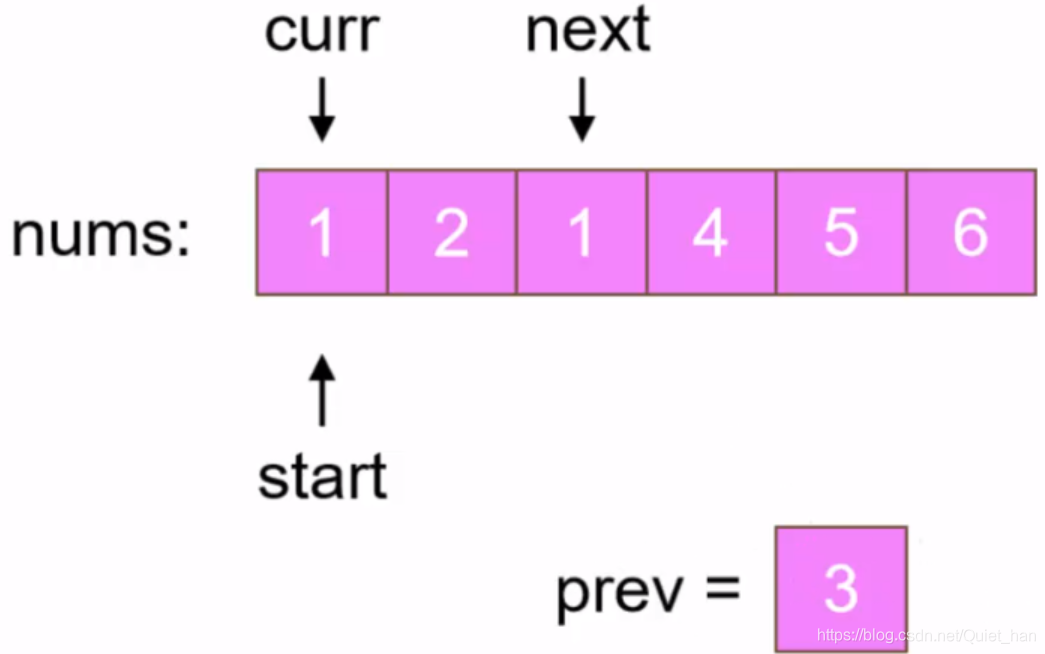
2.3 方案三：数组反转

还是以示例一为例

第一步：先将整个数组反转，反转之后后面三个元素的确是到前面去了，但是还是反的：

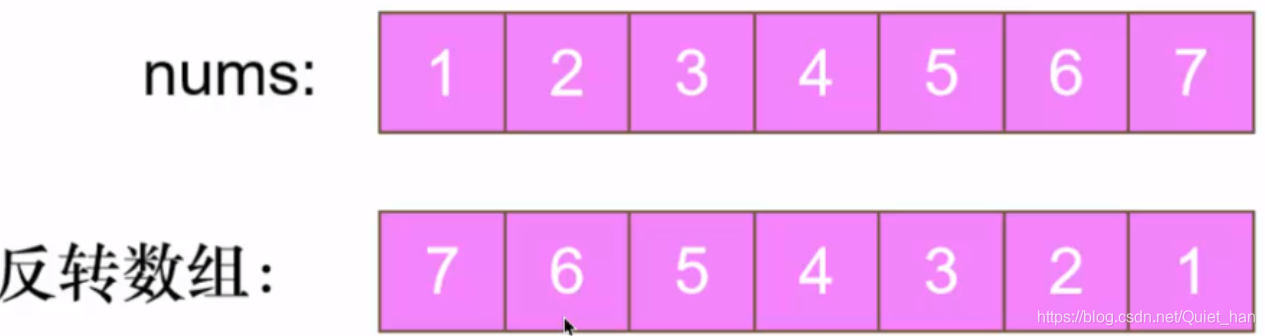
第三步：反转[0,k-1]也就是前面三个元素：

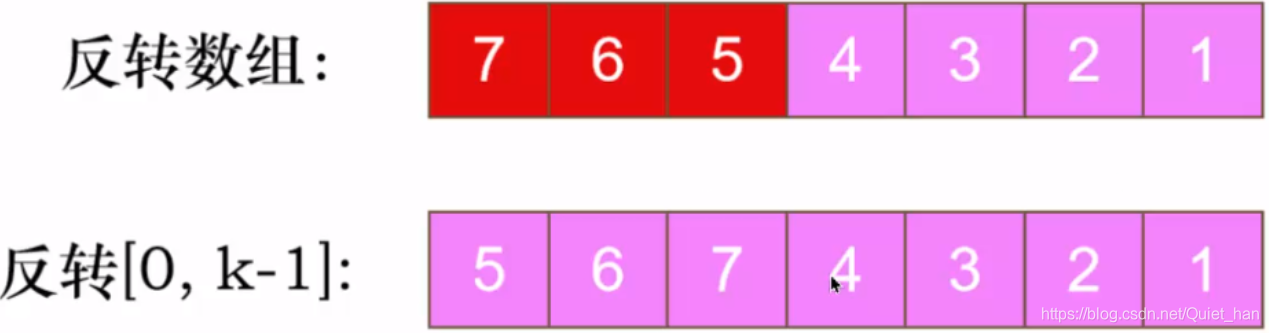
第四步：再反转后面四个元素：

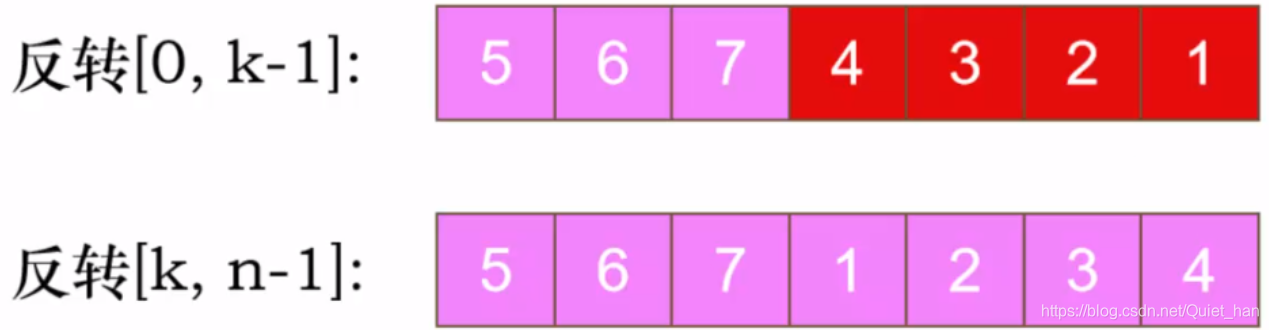
三、代码演示

3.1 使用额外数组

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] newArr = new int[n];
        for (int i=0; i<nums.length; i++){
            //计算每个元素应该移动到那个索引的位置
            int index = (i+k)%n;
            //将这个元素赋值给newArr中索引为index位置上
            newArr[index] = nums[i];
        }
        //将newArr数组从索引为0的位置赋值给nums数组，位置也是从索引为0的位置
        System.arraycopy(newArr,0, nums, 0, n);
    }
}

3.2 环状替换

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        //用来计算处理的元素个数
        int count = 0;
        //start用来标记每一个环的起始点
        for (int start=0; count<n; start++){
            int curr = start;
            int prev = nums[start];
            //循环替换
            do {
                int next = (curr+k)%n;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;

                curr = next;
                count++;
            }while(start != curr);
        }
    }
}

3.3 数组反转

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k = k%n;

        //首先反转整个数组
        reverse(nums,0,n-1);
        //反转前面部分
        reverse(nums, 0,k-1);
        //反转后面部分
        reverse(nums, k, n-1);
    }


    //声明一个方法，用来反转数组
    private void reverse(int[] nums, int start, int end){
        while (start<end){
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }
}