84.除自身以外数组的乘积

一、题目描述

给你一个长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0LynjOvt-1628343493392)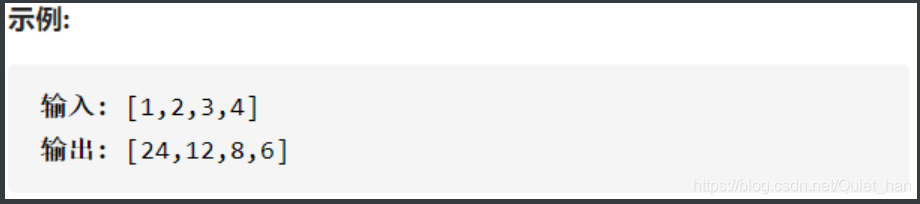
提示：题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内。

说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶：
你可以在常数空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

二、解题思路

方法一：

这道题的思路是对于某个元素，你可以先求出它的左边所有元素的乘积，然后再求出它右边所有元素的乘积。除本身元素以外每个元素的左边元素乘积称之为前缀乘积，右边元素的乘积称之为后缀乘积，可以先把每个元素的前缀后后缀乘积先求出来。

• prefixProduct：对于nums数组中的第一个元素1，它的前缀乘积就是1，第二个元素2的前缀乘积是1，第三个元素3的前缀乘积是1*2=2，第四个元素4的前缀乘积是1*2*3。
• sufixProduct：对于nums数组中的第一个元素1，它的后缀乘积就是2*3*4=24，第二个元素2的后缀乘积是3*4=12，第三个元素3的后缀乘积是4，第四个元素4的后缀乘积是1。
  
  对于遍历的每个元素，要求除它之外的每个元素乘积，只需要将它所在索引对应的前缀后后缀乘积进行相乘不就是索要的结果吗？时间复杂度是O(n)
  
  进阶：
  基于上面的思路，对于前缀乘积，我们就是用题目所给的output数组来存储，就相当于与少开辟一个大小为n的数组来存储前缀乘积，后缀乘积使用一个变量来存储，就不使用数组了，计算每个除本身之外的其它元素乘积时，过程不变，直接看代码演示二。

三、代码演示

代码演示

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;

        //先求所有元素的对应的前缀乘积
        int[] leftProduct = new int[n];
        leftProduct[0] = 1;
        for (int i=1; i<n; i++){
            leftProduct[i] = leftProduct[i-1] * nums[i-1];
        }

        //求所有元素对应的后缀乘积
        int[] rightProduct = new int[n];
        rightProduct[n-1] = 1;
        for (int i=n-2; i>=0; i--){
            rightProduct[i] = rightProduct[i+1] * nums[i+1];
        }
        
        //求每个元素除自身以外所对应的乘积
        int[] output = new int[n];
        for (int i=0; i<n; i++){
            output[i] = leftProduct[i] * rightProduct[i];
        }
        return output;
    }
}

时间复杂度：O(n)

空间复杂度：O(n)，因为开辟了两个数组，并且每个数组空间大小是n，输出的数组不算额外开辟的空间

代码演示二：进阶

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;

        //用output存储前缀乘积
        int[] output = new int[n];
        output[0] = 1;
        for (int i=1; i<n; i++){
            output[i] = output[i-1] * nums[i-1];
        }

        //后缀乘积用一个变量rightProduct来存储，不是数组
        int rightProduct = 1;
        for (int i=n-1; i>=0; i--){
            //计算处本身元素之外的其他元素的乘积
            output[i] = output[i] * rightProduct;
            //更新后缀乘积
            rightProduct = rightProduct * nums[i];
        }
        return output;
    }
}