59.单词拆分

一、题目描述

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

二、解题思路

将这道题翻译一下：如果将字符串s看成是一个背包，单词作为一个个物品，那么这道题就变成了如何取单词能把背包装满，也就是如何取单词能组成字符串s，其中物品（单词可以重复使用，可理解为每个物品无限件），这就相当于一个完全背包问题了。

使用动规五部曲：

第一步：确定dp数组（dp table）以及下标的含义

dp[i]:前 i个字符组成的字符串 s[0..i-1] (或者说字符串长度为i的话)是否能被空格拆分成若干个字典中出现的单词。

第二步：确定递推公式

假设背包中的单词是leetcode，现在dp[i]某个状态是leet（i遍历的长度整好能得出这个），当前的这个状态用dp[j]表示，那么首先我是需要判断dp[j]是否合法，也就是这个leet是不是存在于wordDict中，如果说是存在的，那么我现在再判断dp[i-j]是否也存在wordDict中即可，判断dp[i-j]用字符串的拆分方法就行，使用如下方法：

//表示判断从s中切分的从j到i的单词是否包含在wordDictSet中
wordDictSet.contains(s.substring(j, i))

最后动动态转移方程就是：

if(dp[j] &&  wordDictSet.contains(s.substring(j, i))){
    dp[i] = true;
}

第三步：dp数组如何初始化

从递归公式中可以看出，dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]就是递归的根基，dp[0]⼀定要为true，否则递归下去后⾯都都是false了。

那么dp[0]有没有意义呢？

dp[0]表示如果字符串为空的话，说明出现在字典⾥。但题⽬中说了“给定⼀个⾮空字符串 s” 所以测试数据中不会出现i为0的情况，那么dp[0]初始为true完全就是为了推导公式。下标⾮0的dp[i]初始化为false，只要没有被覆盖说明都是不可拆分为⼀个或多个在字典中出现的单词

第四步：确定遍历顺序

本题的双层for循环先遍历背包还是先遍历物品都是可以的，既不是组合和也不是排列（57_零钱兑换II中有介绍），但是本题中还有特殊性，因为是要求⼦串（比较的是s中每个切分部分），最好是遍历背包放在外循环，将遍历物品放在内循环。如果要是外层for循环遍历物品，内层for遍历背包，就需要把所有的⼦串都预先放在⼀个容器⾥（也就是将s中每种切分的情况对应的字串都先放在一个容器中）。

代码如下：

for(int i=1; i<=s.length(); i++){  //遍历背包
    for(int j=0; j<i; j++){  //遍历物品
        if(dp[j] && wordDictSet.contains(s.substring(j,i))){
            dp[i] = true;
            break;
        }
    }
}

第五步：举例推导dp数组

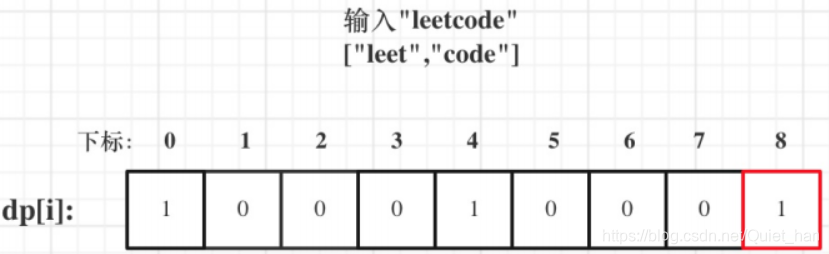
三、代码演示

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        HashSet<String> wordDictSet = new HashSet(wordDict);

        //创建dp
        boolean[] dp = new boolean[s.length()+1];

        //初始化dp
        dp[0] = true;

        //遍历循环
        for(int i=1; i<=s.length(); i++){  //遍历背包
            for(int j=0; j<i; j++){  //遍历物品
                if(dp[j] && wordDictSet.contains(s.substring(j,i))){
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }
}