60.多重背包_60升的背包是多少-优快云博客

本文介绍了如何将背包问题扩展到多重背包场景，通过举例说明多重背包与01背包的相似性。文章提供了一个Java代码实现，展示了如何处理每种物品可拥有多个的情况，并通过动态规划求解最大价值。在代码中，首先处理每种物品的个数，然后应用01背包的策略进行优化。最后，给出了完整的多重背包解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

前言
一、问题描述
二、解题思路
三、代码演示

前言

多重背包在力扣中也没有对应的题目，这里做一个知识扩展，有些题目可以转换成多重背包去解决。

一、问题描述

有N种物品和⼀个容量为V 的背包。第i种物品最多有M(i)件可⽤，每件耗费的空间是C(i)，价值是W(i)。求解将哪些物品装⼊背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最⼤。多重背包和01背包是⾮常像的，为什么和01背包像呢？

每件物品最多有M(i)件可⽤，把M(i)件摊开，其实就是⼀个01背包问题了。

例如：

背包最大重量为10.

物品为：

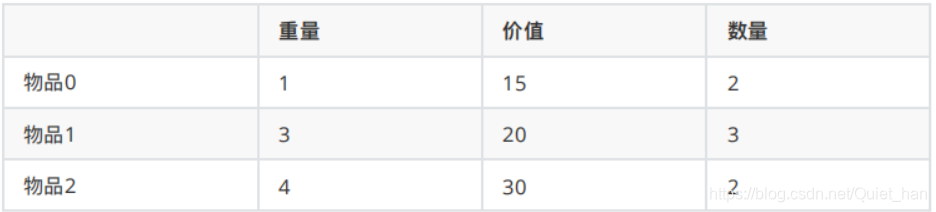
在这里插入图片描述

问背包能背的物品最⼤价值是多少？和如下情况是没区别的：
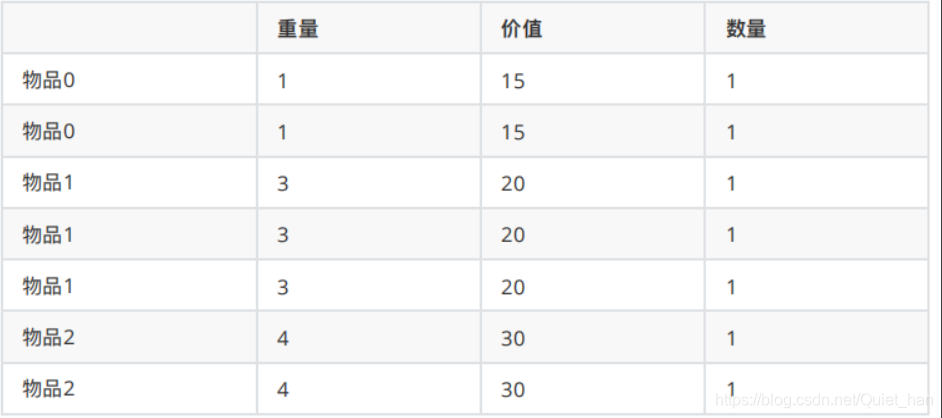
在这里插入图片描述

二、解题思路

其实与01背包的区别不大（49_01背包问题），只是多加了一个方法来计算可选物品的个数，因为每种物品的个数都不只是一个。

详细见代码部分。

三、代码演示

package multiPack;

public class Solution {
    public static void main(String[] args) {
        //主方法
        //背包最大容量
        int bagWeight = 10;

        //表示每种物品的重量
        int weight[] = {1,3,4};
        //每个物品的价值
        int value[] = {15, 20, 30};
        //每种物品的数量
        int nums[] = {2, 3, 2};

        //调用方法传值
        mulPack(weight,value, nums, bagWeight);

    }

    //写一个打印结果的方法
    public static void Print(int[] a) {
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i] + " ");
        }
    }


    //这个方法主要是背包的实现
    public static int[] BackPack_Solution(int bagWeight, int[] weight, int[] value) {
        //dp[i][j]表示前i件物品恰放入一个重量为m的背包可以获得的最大价值
        int dp[] = new int[bagWeight + 1];

        //dp数组的初始化
        for (int j = bagWeight; j >= weight[0]; j--) {
            dp[j] = dp[j - weight[0]] + value[0];
        }

        //遍历部分
        for (int i = 1; i < weight.length; i++) {  //遍历物品
            for (int j = bagWeight; j >= weight[i]; j--) { //遍历背包，注意这里是倒叙
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
            //调用Print打印方法打印每轮循环遍历的结果
            Print(dp);
            System.out.println();
        }
        return dp;
    }

    //下面这个方法实现的是每种物品的个数和价值的赋值
    public static int[] mulPack(int[] weight, int[] value, int[] nums, int bagWeight){
        //记算一共有多少个物品，每种物品*每种物品的个数就是总的物品数
        int sum = 0;
        for (int i=0; i< nums.length; i++){
            sum += nums[i];
        }

        //表示每个物品的重量，注意不是每种是每个
        int[] weightSum = new int[sum];
        //表示每个物品的价值
        int[] valueSum = new int[sum];

        int left = 0;
        for (int i=0; i<weight.length; i++){  //遍历每种物品
            for (int j=1; j<=nums[i]; j++){  //每种物品的个数是nums[i],遍历每个物品
                //给每个物品赋上它所属种类对应的重量
                weightSum[left] = weight[i];
                //给每个物品赋上它所属对应种类的价值
                valueSum[left] = value[i];
                left++;
            }
        }
        //将结果作为参数传递给BackPack_Solution方法
        return BackPack_Solution(bagWeight,weightSum,valueSum);
    }
}