从管理学本科水平开始的统计学进阶

原创已于 2025-03-31 09:04:02 修改 · 873 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #统计学 #数学

于 2023-01-16 13:38:21 首次发布

数学学习笔记专栏收录该内容

6 篇文章

订阅专栏

本文介绍了统计学的基础概念，包括数据类型、科学术语、分布和假设检验。通过Python代码展示了如何进行T检验、相关性检验（Pearson、Spearman和Kendall）以及正态分布检验（Shapiro-Wilk、DAgostinosK2和Anderson-Darling）。文章适合管理学背景的学习者，帮助他们从实战角度掌握统计分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

诸神缄默不语-个人优快云博文目录

（管理学本科水平：指本科学了个锤子的管理学专业毕业生开始从0开始学习统计学）

1. 数据类型

categorical / integer

详情请参考我写的另一篇博文：测量尺度：名义尺度、定序尺度、定距尺度和定比尺度

2. 科学术语

无放回抽样sampling without replacement
偏倚
偏度是对数据分布对称性的测度，衡量数据分布是否左偏或右偏。
峰度是对数据分布平峰或尖峰程度的测度，它是一种简单而常用的正态性统计检验量。
长尾
列联表 / 交互分类表：按照两至多个属性进行分类，列出频数表¹
独立成分分析ICA
统计推断statistical inference
1. 参数估计parameter estimation
2. 假设检验
3. bootstrap：一种抽样方法。大概来说就是放回抽样多次，用多次抽样的指标的平均值作为最终的指标²

3. 分布

正态（高斯）分布
泊松分布

4. 假设检验

1. 参数检验 / 一致性评价

各种用以衡量两组数据是否一致的方法

学生T检验
用于检验两独立样本数据的均值是否存在显著差异。
使用前提：1. 各样本观察值为独立同分布的 2. 样本数据服从正态分布 3. 每个样本观测值的方差相等

from scipy.stats import ttest_ind
data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
stat, p = ttest_ind(data1, data2)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
    print('不能拒绝原假设，两样本集分布相同')
else:
    print('拒绝原假设，样本集分布可能不同')

Bland-Altman分析 / BA分析³：主要用于比较两种不同的测量方法或工具对相同样本的测量准确性和一致性

2. 相关性检验

各种用以衡量两组数据是否相关的方法

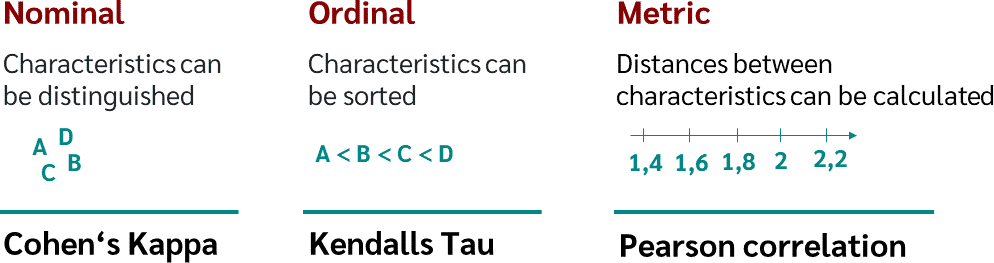
在这里插入图片描述

1. 数值变量

皮尔生(Pearson)乘积矩相关系数r / 皮尔逊相关系数 / 皮尔逊积矩相关系数 / PPMCC / PCCs：衡量线性相关性的强度

该检验将两个变量之间的协方差进行归一化处理以给出可解释的分数，为一个介于-1到1之间的值，-1表示完全负相关，1表示完全正相关，0表示没有相关性。
使用前提：1. 各样本观察值为独立同分布的 2. 样本数据服从正态分布 3. 每个样本观测值的方差相等
原假设：两变量相互独立

PEARSON 函数 - Microsoft 支持

from scipy.stats import pearsonr
data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
data2 = [0.353, 3.517, 0.125, -7.545, -0.555, -1.536, 3.350, -1.578, -3.537, -1.579]
stat, p = pearsonr(data1, data2)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
    print('两变量相互独立')
else:
    print('两变量可能存在线性相关关系')

Spearman等级相关
用于检验两变量是否具有单调关系。
当两变量因非线性关系相关，或者不服从正态分布时，Spearman相关系数可以用来反映变量间的相关性强度。如果存在线性关系，也可以使用这种方法来检验，但是可能导致计算出的相关系数较低。
Spearman不是使用样本数据本身的协方差和标准差来计算相关系数的，而是根据样本值的相对秩次来计算统计量，这是非参数统计中常用的方法。
使用前提：1. 各样本观察值为独立同分布的 2. 各样本数据可定序

from scipy.stats import spearmanr
data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
data2 = [0.353, 3.517, 0.125, -7.545, -0.555, -1.536, 3.350, -1.578, -3.537, -1.579]
stat, p = spearmanr(data1, data2)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
    print('两变量相互独立')
else:
    print('两变量可能存在相关关系')

Kendall等级相关
用于检验两变量是否具有单调关系。
使用前提：1. 各样本观察值为独立同分布的 2. 各样本数据可定序

from scipy.stats import kendalltau
data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
data2 = [0.353, 3.517, 0.125, -7.545, -0.555, -1.536, 3.350, -1.578, -3.537, -1.579]
stat, p = kendalltau(data1, data2)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
    print('两变量相互独立')
else:
    print('两变量可能存在相关关系')

2. 分类变量

Chi-Squared Test卡方检验：用于检验两分类变量是否相关。
卡方检验的零假设是一个分类变量的观测频数与该分类变量的期望频数相吻合。检验统计量服从卡方分布。
使用前提：用于计算两变量的列联表的观测值是独立的
列联表的每个单元格的期望计数不小于5
原假设：两变量相互独立

from scipy.stats import chi2_contingency
from scipy.stats import chi2

# 列联表
table = [[10, 20, 30],
        [6,  9,  17]]
print('列联表')
print(table)

stat, p, dof, expected = chi2_contingency(table)
print('自由度dof=%d' % dof)
print('期望分布')
print(expected)

# [[10.43478261 18.91304348 30.65217391]
#  [ 5.56521739 10.08695652 16.34782609]]

# 采用统计量推断
prob = 0.95
critical = chi2.ppf(prob, dof)
print('probability=%.3f, critical=%.3f, stat=%.3f' % (prob, critical, stat))
if abs(stat) >= critical:
    print('拒绝原假设，两变量存在相关关系')
else:
    print('不能拒绝原假设，两变量相互独立')

# 采用p值推断
alpha = 1.0 - prob
print('significance=%.3f, p=%.3f' % (alpha, p))
if p <= alpha:
    print('拒绝原假设，两变量存在相关关系')
else:
    print('不能拒绝原假设，两变量相互独立')

Cohen’s kappa coefficient：用于度量单标签任务中两个打分者打的分的相似程度（inter-rater reliability），好像做数据标注的时候用这个多。⁴

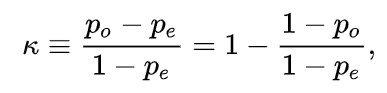
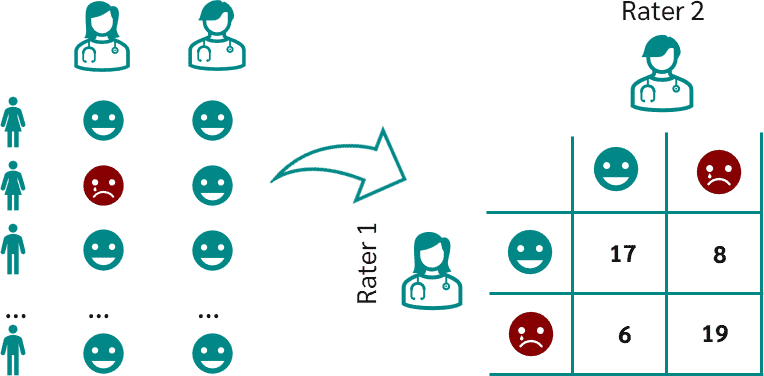
$p_o$ （observed）是两个rater打分相同的频率（accuracy）：
$p_o=\frac{17+19}{17+8+6+19}=72\%$

$p_e$ （expected）是假设两个rater完全独立随机打分时，两个rater打分打出这么多相同打分的概率（每个rater打每个类别的分的频率相乘，再加起来）。可以视作baseline，Kappa指标就是衡量实际频率比这个baseline概率高多少：

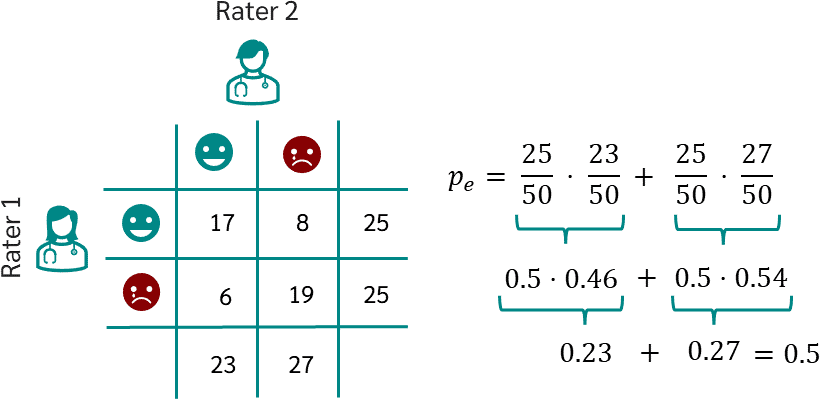
另一种计算逻辑是：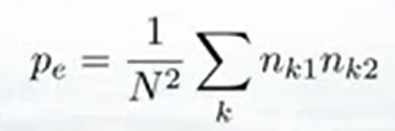
对二分类来说，Kappa公式也可以写成：

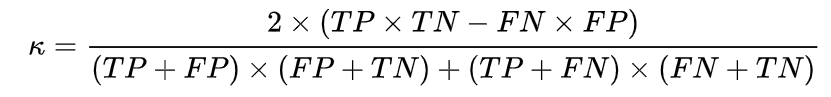
本案Kappa计算结果为：
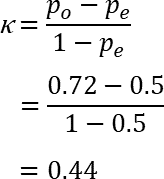
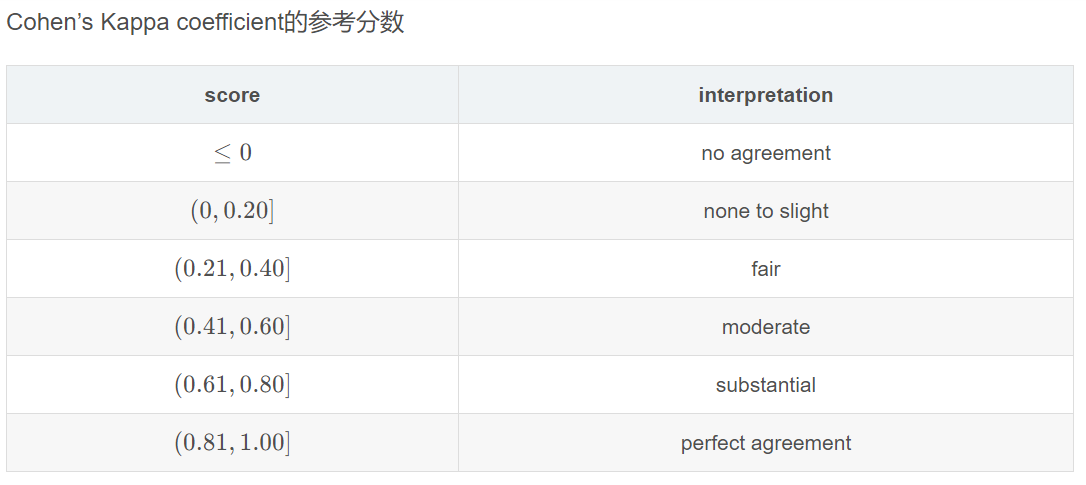
weighted kappa
相当于在混淆矩阵上对每个值都乘一个权重，或者说用混淆矩阵点乘一个权重矩阵。
在有顺序的多标签分类问题上：
Linear Weighted Kappa：误差系数等于两个label之间差的绝对值，如将1预测为3误差权重为2
Quadratic Weighted Kappa：误差系数等于两个label之间差的平方，如将1预测为3误差权重为4

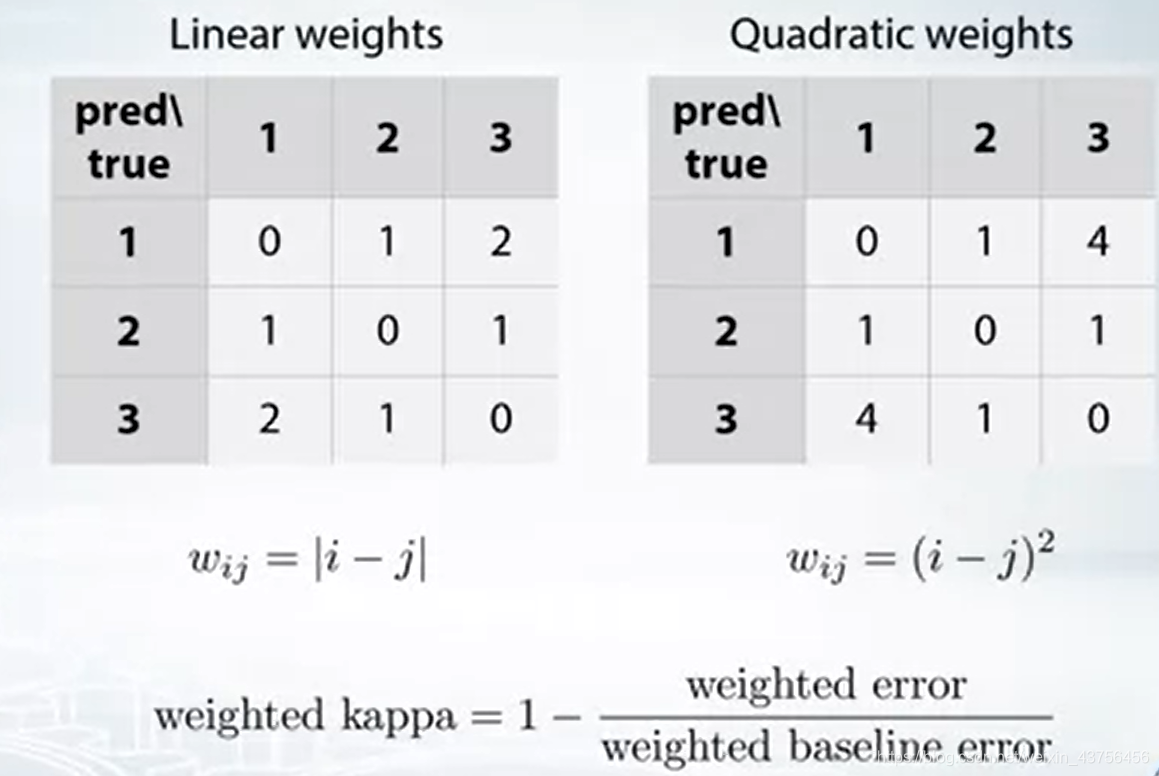
cohen_kappa_score — scikit-learn 1.7.dev0 documentation中就集成了这两种权重计算方式。

3. 显著性检验

方差检验ANOVA
1. one-way ANOVA

4. 正态分布检验

Shapiro-Wilk Test (W 检验)：用于检验样本数据是否来自服从正态分布的总体
在实际应用中，W 检验被认为是一个可靠的正态性检验，但是也有人认为该检验更适用于较小的数据样本（数千个观测值以内）。
使用前提：各样本观察值为独立同分布的

from scipy.stats import shapiro
data = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
stat, p = shapiro(data)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
    print('不能拒绝原假设，样本数据服从正态分布')
else:
    print('不服从正态分布')

D’Agostino’s $K^2$ Test：用于检验样本数据是否来自服从正态分布的总体。
D’Agostino’s $K^2$ Test是通过计算样本数据的峰度和偏度，来判断其分布是否偏离正态分布。
使用前提：各样本观察值为独立同分布的

from scipy.stats import normaltest
data = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
stat, p = normaltest(data)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
    print('不能拒绝原假设，样本数据服从正态分布')
else:
    print('不服从正态分布')

Anderson-Darling Test：用于检验样本数据是否服从某一已知分布。
该检验修改自一种更复杂的非参数的拟合良好的检验统计（Kolmogorov-Smirnov Test）。SciPy中的anderson()函数实现了Anderson-Darling检验，函数参数为样本数据及要检验的分布名称，默认情况下，为’norm’正态分布，还支持对’expon’指数分布，'logistic’分布，以及’gumbel’耿贝尔分布的检验，它会返回一个包含不同显著性水平下的p值的列表，而不是一个单一的p值，因此这可以更全面地解释结果。
使用前提：各样本观察值为独立同分布的

from scipy.stats import anderson
data = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
result = anderson(data)
print('stat=%.3f' % (result.statistic))
for i in range(len(result.critical_values)):
    sl, cv = result.significance_level[i], result.critical_values[i]
    if result.statistic < result.critical_values[i]:
        print('显著性水平为%.2f时，P值为%.1f,不能拒绝原假设，样本数据服从正态分布' % (sl/100, cv))
    else:
        print('显著性水平为%.2f时，P值为%.1f, 拒绝原假设，样本数据不服从正态分布' % (sl/100, cv))

5. 统计绘图（附Python 3代码）

我另外写了一篇博文，请参考：Python 3统计绘图简单示例

6. 统计指标

1. 描述一组数据

均值
1. 算术平均值
2. 调和平均值
中位数
方差
标准差
医学领域的独特指标
1. Positive Predictive Value (PPV)

2. 评估模型预测结果

混淆矩阵 / 混淆表 / 误差矩阵：有监督学习预测结果的可视化
是一种特殊的（二维的）列联表⁵
准确率accuracy
精度precision
召回率recall / 灵敏度sensitivity： $\frac{TP}{TP+FN}$
F值
特异性specificity： $\frac{TN}{TN+FP}$
ROC
Youden’s $J$ static / deltaP’ / 知情性informedness：衡量模型是不是纯纯瞎猜的，就不管是谁都是一样的输出概率（取值范围为[-1,1]）

⁶