为何叫SVM支持向量机？及其有关求解实例

目录

1、距离的计算 

2、数据标签的定义

3、优化目标

4、目标函数

5、拉格朗日乘子法

7、SVM求解

8、求偏导SVM求解

SVM求解实例

为何叫支持向量机？

实验现象：

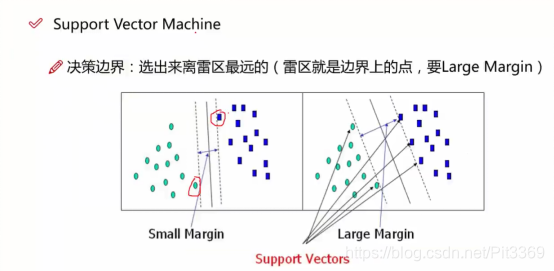
当支持向量没有变化，无论添加多少样本数据，对最终的决策边界是没有影响的。

---

 超详细版数学推导过程见：https://blog.youkuaiyun.com/Pit3369/article/details/88941100

1、距离的计算 

 

 

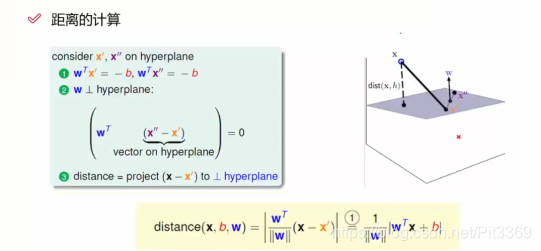
注解：

1. W：垂直于平面的法向量
2. 点x’ x’’均在平面内，故满足平面方程，代入化简得出式子1
3. (x’’-x’)表示平面内部的直线，“平面的法向量垂直于平面内的任意一条直线”，故得出式子2
4. 点x到平面的距离，可等价于，一条直线(x-x’)相对于平面的竖直投影(dist)

向量X/模(X)==单位向量，竖直单位向量*直线(x-x’)长度==点x到平面的距离

又因为x’未知，但x’满足超平面方程，代入化解，得出最后结果

2、数据标签的定义

 

注解：

1. Xi是数据集，Yi是标签。
2. X正例,Y>0;X负例,Y<0。二化为一==数据X、标签Y同号时>0

3、优化目标

 

注解：

1. 通俗解释：找到一条超平面，使得最近的点到该平面的距离相对的足够大
2. 上一页PPT最后将两种情况归一化，使得Yi*Y(xi)恒>0，故可去掉绝对值。

4、目标函数