Coding | [代码随想录][动态规划] 494.目标和

最新推荐文章于 2025-12-07 21:20:15 发布

原创最新推荐文章于 2025-12-07 21:20:15 发布 · 898 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #leetcode #数据结构

题面

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

思路

做了一小部分动态规划题目，初步印象是其难点就在于五部曲中的第一步：

确定dp数组结构、含义以及其下标的含义。

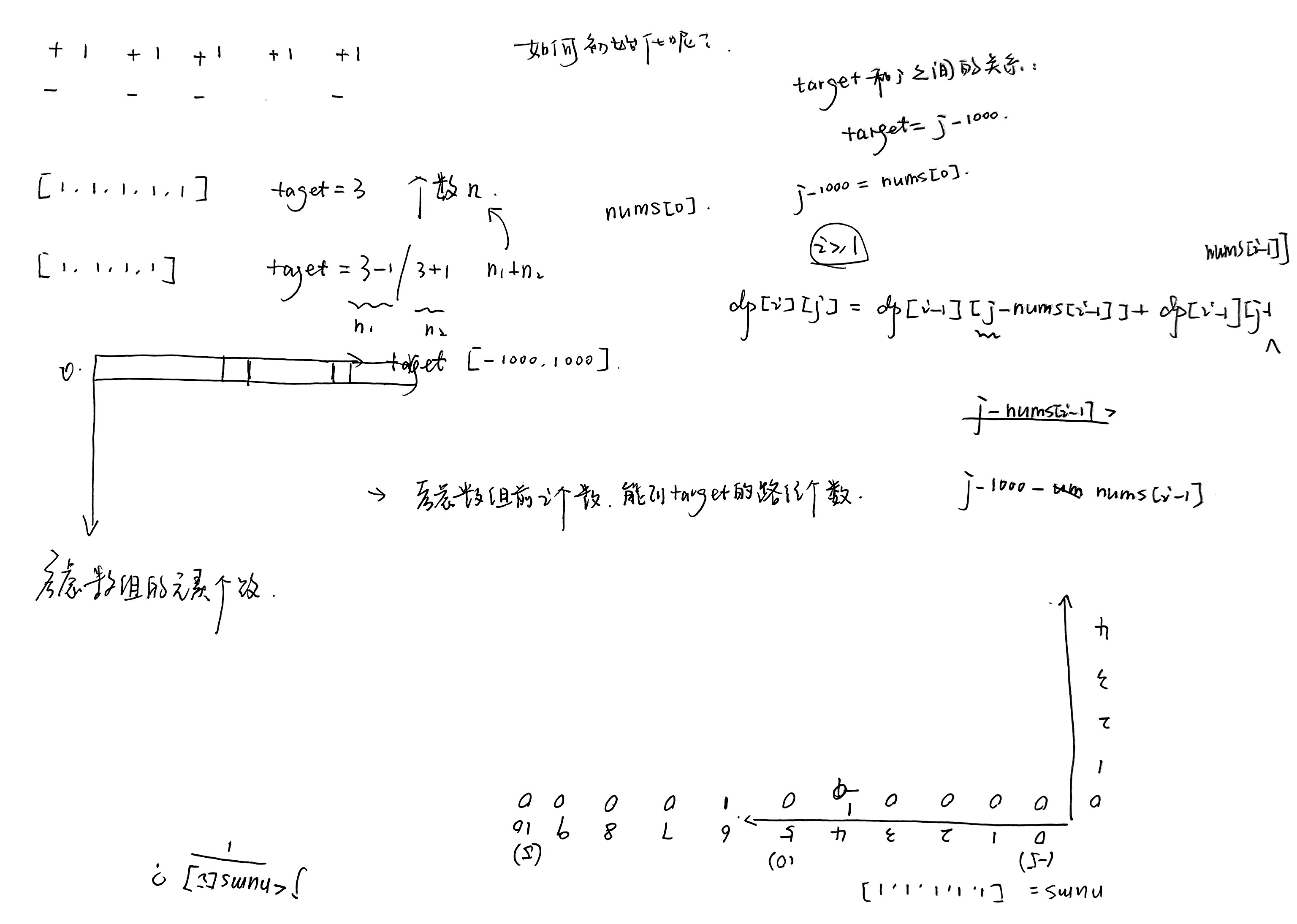
在这里我按照Carl说的，在寻找怎么样构造dp数组(aka Step1)，而怎样构造dp数组也根本取决于能不能产生出一个可以递推迭代的子问题/子表达式。

我的演草纸的左上角便是这一部分的一些探索痕迹。即：target为3的前五个数的表达式个数可以表示为target为2或4的前四个数表达式个数之和。

那接下来其实怎样构造一个dp数组也不成问题了。可以看作一个0-1背包问题，构造一个二维dp数组。而之后的：如何初始化、遍历顺序的确定也就呼之欲出。

调试

其实在这一篇我真正想传达的，是Carl所说的动态规划的调试方法——举例演算。

代码随想录https://www.programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E5%BA%94%E8%AF%A5%E5%A6%82%E4%BD%95debug

思路的清晰设计让我在编码过程中十分顺利，但是一次编码就ac对我来说还是很困难的。有一些大大小小的问题，我都是通过实际举例去手动演算，发现我的代码逻辑和真实的算法逻辑之间的差异。

初始化。我最开始是将dp数组所有初始化为INT_MIN，然后对第一排(i = 0)初始化：nums[i]为正负的时候，dp值为1。这就忽略了±0皆为0的情况，后面就改成了所有初始化为0，满足条件则++。
边界设置。最开始设置边界为题目中规定的[-1000, 1000]，后面发现最大最小也就取决于数组总和，为了控制空间大小，也做了改进。
dp数组更新时的边界处理。最开始我直接把dp数组中超限的元素给置为0，但是调试过程中发现只需要将超限的一半边置为0即可，另一边一样是可以得来的。这也是通过实际模拟发现的逻辑失误。

题解

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int totalSum = 0;
        for(int i = 0; i < nums.size(); i++){
            totalSum += nums[i];
        }
        vector<vector<int>> dp(nums.size(), vector<int>(2 * totalSum + 1, 0));
        for(int j = 0; j < dp[0].size(); j++){
            if(j == totalSum - nums[0]) dp[0][j]++;
            if(j == totalSum + nums[0]) dp[0][j]++;
        }
        for(int i = 1; i < nums.size(); i++){
            for(int j = 0; j < dp[0].size(); j++){
                int left, right;
                if(j < nums[i]) left = 0;
                else left = dp[i - 1][j - nums[i]];
                if(j >= dp[0].size() - nums[i]) right = 0;
                else right = dp[i - 1][j + nums[i]];
                dp[i][j] = left + right;
            }
        }
        if(target + totalSum < 0 || target + totalSum >= dp[0].size()) return 0;
        return dp[nums.size() - 1][target + totalSum];
    }
};

时间复杂度：O(n*totalSum)，空间复杂度：O(n*totalSum)