代码随想录-01|Prepare、数组理论、704.二分查找、27.移除元素

Before Coding

代码随想录
我们在写代码时要注意一些常识：

• a[i++]指的是取完元素a[i]后，再对i进行自增1
• a[++i}指的是先对i自增1，再取元素
• expression1 && expression2，先对expression1进行判断，如果为假就不再进行expression2的判断
• expression1 || expression2，先对expression1进行判断，如果为真就不再进行expression2的判断

总建议

每日精华：

1. 保持刷题节奏（时间紧张可以只AC，时间缺失要抽出时间查看当天题解思路）。
2. 题目可以钻研但不要死磕，因为刷题会有3刷4刷，每一遍的brush会让当初的桎梏化为灰烬，科研是攻坚克难，Coding需要高效输出。
3. 先看视频，事半功倍；不看视频，深度思考。
4. 新手刷题遇到奇怪bug代码全删连备份都不要，原因：这种情况下多数是很低级的手误，比如符号的全角半角，少了一个字母那种的，自己去看很难发现，即便花时间排查出来了也没有什么提高。
5. 多考虑代码鲁棒性， 进入循环打一下日志啥，是很好的一个发现错误的方法。
6. 输出语句debug一下力扣支持,遇到问题一般自己先输出debug,解决不了设计简单case手动debug(一定要是简单case,因为手动理解深但是麻烦),再解决不了群里问别人这样是比较好的,debug也是我们写算法的一个能力,这个能力和边界case的思维对大家的工作也会有一些帮助。

How to Debug？

四个层次，由易到难：

1. 直接对照代码随想录文章中的示例代码，一行行对比看看自己哪里与之不同。看起来是最笨的办法，但是如果你是初学者，通过这个过程可以很快发现自己与好的代码之间的差距，对能力提升也非常快。
2. ChatGPT 或者 new bing 等新 AI 工具，在与其对话中找出代码 bug 并解决自己的其它疑惑。
3. 打印日志到控制台输出并通过观察它们来找出问题所在，下面会给出示例。
4. 使用 IDE 的断点调试功能，学会在代码中打断点然后单步执行，所有变量的中间值一目了然，bug 自然无所遁形，这也是实际工作中常用debug的方式。

• 关于debug：
  • 说明：利用idea或者其他编辑器自带的断点和debug工具调试,当然可以细化debug的粒度,记住核心是先定位问题的行数,出现的轮次,在那个轮次当中进行检查

例子1 for内部出现问题

// for内部出现问题
for (int i = 0; i < n; i++) {
	std::cout << i << " " << "需要查看的变量" << std::endl;
	// 一系列逻辑操作,注意i是必须要有的可以看轮次,如果一系列操作出出现了异常可以定位出第几次
	std::cout << i << " " << "需要查看的变量" << std::endl;
	// 定位出第几次出现异常后,我们就可以细化粒度, 每一个操作逻辑打一个输出语句同时记得标记轮次
}

例子2 链表异常，空针异常建议打法

// 链表异常，空针异常建议打法
ListNode list = new ListNode(传入的值);
ListNode next = list.next;
int cnt = 0;	// 标记轮次
while (逻辑判断) {
	std::cout << cnt << " " << list.val << " " << next.val << " " << "想要查看的变量"  << std::endl;	// 出现空针异常可以看一下上一轮的值
	cnt++;
	std::cout << list.next ==next << << 一系列可能引起空针或者环的操作或者值或者地址 << std::endl;
}

例子3 数组越界问题

// 数组越界问题
int cnt = 0;
while (True) {
	std::cout << cnt << " " << 下标 << std::endl;
	用到下标的任意代码
	std::cout << cnt << " " << 下标 << std::endl;
}

例子4 判断是否进入if

// 判断是否进入if
if () {
    // 任意输出
}
// 如果没进入在if上面打输出语句看你的变量是否正确

例子5 树递归

int cnt = 0;
void f (TreeNode root) {
	if (root == null) std::cout << cnt << std::endl; // 放空针异常
	else std::cout << root.val << " " << cnt << std::endl;
	cnt++;
	if (root == null) std::cout << cnt << std::endl; // 放空针异常
	else std::cout << root.val << " " << cnt << std::endl;
	cnt++;
}
// 再来个层序
while (!q.empty()) {
	//任何获取到TreeNode后的操作和需要用到TreeNode的地方之前打一个输出即可
	f(查看的tree node);
    //操作前操作后都需要打！！！！！！！！！！！ 
}

其他情况

• 一个排查问题的思路: 报错一大串, 也分不清是哪里出错了，这种情况下，你把你的函数一个一个的删（当然之前可以先备份一下），删到哪个函数，没报错了，再去填新的函数，不要整段代码一起看。
• 对于debug 还是大家在自己不理解的地方, 预期不一样的地方之前打一下输出语句就可以了, 因为可能方法没完全理解等问题 。
• 递归的程序用什么方法DEBUG比较好：
  • 第几层的话可以用一个全局变量来记录。每进一层就给这个变量+1，然后顺带把这一层的数据打印出来。当然这个变量也要回溯。

关于题解

题解可以提高刷题效率，通过对比可以高效排错，一般出现bug的地方也只是一些微小的细节，注意得多了自然以后经验丰富了bug率自然也会降低的。

刷题技巧

• 根据题目的数据量范围选择合适的算法，比如数据量是$10^5$，那就只能使用$O(nlogn)$复杂度以下的算法了，使用$O(n^2)$是会超时的；而如果数据量只有100或者1000，则可以果断的采用暴力方法（一般是$O(n^2)$）进行求解。
• 为了特殊情况专门写判断语句？是否需要考虑特殊的情况？
  需要考虑特殊情况，比如容器/数组/指针是否为空等，可以在考虑到特殊情况后先额外判断写出来，整体逻辑写完后看是否能和一般情况进行合并。
• while复杂度分析主要看内部总共执行多少次,for嵌套就成了$O(n^2)$,滑动窗口就是$O(n)$
• 涉及到修改字符串的O(1)算法理论上是只对字符串可以修改的编程语言成立的(如C++)，对于其他编程语言通常参数会给成字符数组的形式
• 对于常数级别复杂度的讨论：不需要纠结固定的什么数量级的复杂度，要从算法的整体复杂度上去考虑。开一千的空间，对于百万的数据量，它就是常数。但对于同样是几千甚至是几百的数据量，认为开这样一个空间是O(1)的复杂度从而认为是一个好的算法明显是不正确的。
• 8/9 明日更

关于 神龍Str 的博客

在record学习的过程中，博主会刻意挖掘问题以Q的形式呈现，并附在每篇博客的最后。这些Q可能是关于基础概念的，可能覆盖八股，也可能是关于一些算法的深入思考，最后会在代码-春秋中给出答案A，包含了一些官方概念或者博主的思考。

---

数组理论基础

数组是非常基础的数据结构，在面试中，考察数组的题目一般在思维上都不难，主要是考察对代码的掌控能力。

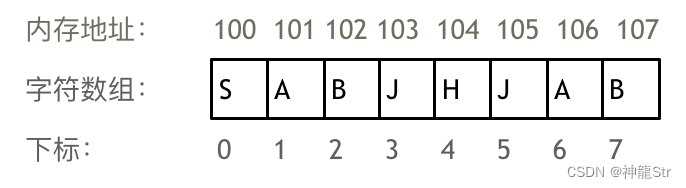
• Q:什么是数组
  数组是存放在连续内存空间的相同数据类型的集合。
  

• Q:数组特性

  • 数组的下标是从0开始的。
  • 数组的内存空间是连续的。
  • 因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。
  • 数组的元素是不能删的，只能覆盖。
  • 注意vecotr和array的区别，vector是容器，底层是通过array实现的。

• 关于二维数组
  

  • Q:二维数组的空间是否连续
    不同编程语言的内存管理是不一样的，以C++为例，在C++中二维数组是连续分布的。

    以cpp为例：

    void test_arr() {
        int array[2][3] = {
    		{0, 1, 2},
    		{3, 4, 5}
        };
        cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
        cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
    }
    
    int main() {
        test_arr();
    }
    

    输出结果：

    0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
    0x7ffee406582c 0x7ffee4065830 0x7ffee4065834
    

    以16进制为例，4个字节，二维数组的地址是连续的0x7ffee4065828 与 0x7ffee406582c 也是差了4个字节，在16进制里8 + 4 = c，c就是12。
    

    补充：像Java是没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。

    public static void test_arr() {
        int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
        System.out.println(arr[0]);
        System.out.println(arr[1]);
        System.out.println(arr[2]);
        System.out.println(arr[3]);
    }
    

    输出地址为：

    [I@7852e922
    [I@4e25154f
    [I@70dea4e
    [I@5c647e05
    

    这里的数值也是16进制，这不是真正的地址，而是经过处理过后的数值了，我们也可以看出，二维数组的每一行头结点的地址是没有规则的，更谈不上连续。

    

Let’s Code

704.二分查找

Q:二分查找使用条件：
这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

Q:二分查找边界定义：

• 左闭右开
• 左闭右闭

算法关键：
二分查找涉及的很多的边界条件，例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

左闭右闭[left, right] ：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
  

左闭右开[left, right)：

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

middle计算时关于(right + left) / 2向下取整

由于middle = (right + left) / 2操作是向下取整，因此在二分到只剩下两个元素区间时注意是向左移动还是向右移动：

• 如果是向左移动，可以直接令right = middle，因为向下取整会自动向左改变下标
• 如果是向右移动，此时middle为向下取整结果，需要加1来完成向右移动left = middle + 1

在本次题目中实现了对向下取整的考虑，当然代码随想录其实用wihle中的逻辑判断已经避免了考虑除法向下取整的case，也可以ac。

代码随想录题解：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

我的题解：

class Solution {
public:
    int search(vector<int>& nums, int target) {

        int mid_idx;
        int up_bound = nums.size() - 1, down_bound = 0;

        if (target < nums[0] || target > nums[nums.size() - 1]) {
            return (-1);
        }
        
        while (up_bound != down_bound) {
            mid_idx = (up_bound + down_bound) / 2;
            if (nums[mid_idx] == target) return (mid_idx);
            else if (nums[mid_idx] < target) down_bound = mid_idx + 1;
            else up_bound = mid_idx;
        }

        // 如果最后范围限定到了最后两个数或者一个数
        if (nums[down_bound] == target) return down_bound;
        else return (-1);
    }
};

27.移除元素

本题较为简单，思路明确，应熟练掌握自增自减运算符

自增自减运算符

Q:双指针的形式

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作

Q:快慢指针

• 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
• 慢指针：指向更新 新数组下标的位置
  
  gif

代码随想录双向指针法：

/**
* 相向双指针方法，基于元素顺序可以改变的题目描述改变了元素相对位置，确保了移动最少元素
* 时间复杂度：O(n)
* 空间复杂度：O(1)
*/
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int leftIndex = 0;
        int rightIndex = nums.size() - 1;
        while (leftIndex <= rightIndex) {
            // 找左边等于val的元素
            while (leftIndex <= rightIndex && nums[leftIndex] != val){
                ++leftIndex;
            }
            // 找右边不等于val的元素
            while (leftIndex <= rightIndex && nums[rightIndex] == val) {
                -- rightIndex;
            }
            // 将右边不等于val的元素覆盖左边等于val的元素
            if (leftIndex < rightIndex) {
                nums[leftIndex++] = nums[rightIndex--];
            }
        }
        return leftIndex;   // leftIndex一定指向了最终数组末尾的下一个元素
    }
};

Q

Q:什么是数组
Q:数组特性
Q:二分查找使用条件
Q:二分查找边界定义
Q:自增自减运算符
Q:双指针的形式
Q:快慢指针