Coding | [代码随想录][贪心] 968.监控二叉树

题面

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

思路

从拿到题一脸懵逼开始，再到彻底放弃，其实我也算做了一些尝试。比如：

1. 叶结点一定不是摄像头
2. 叶结点的父结点一定是摄像头
3. 摄像头与摄像头之间应该隔了两代

但是我在尝试的过程中把二叉树过于理想化，将结点层作为算法的基本单位考虑了。这肯定是不对的。当我认知到这个问题的时候，便果断看题解去了。

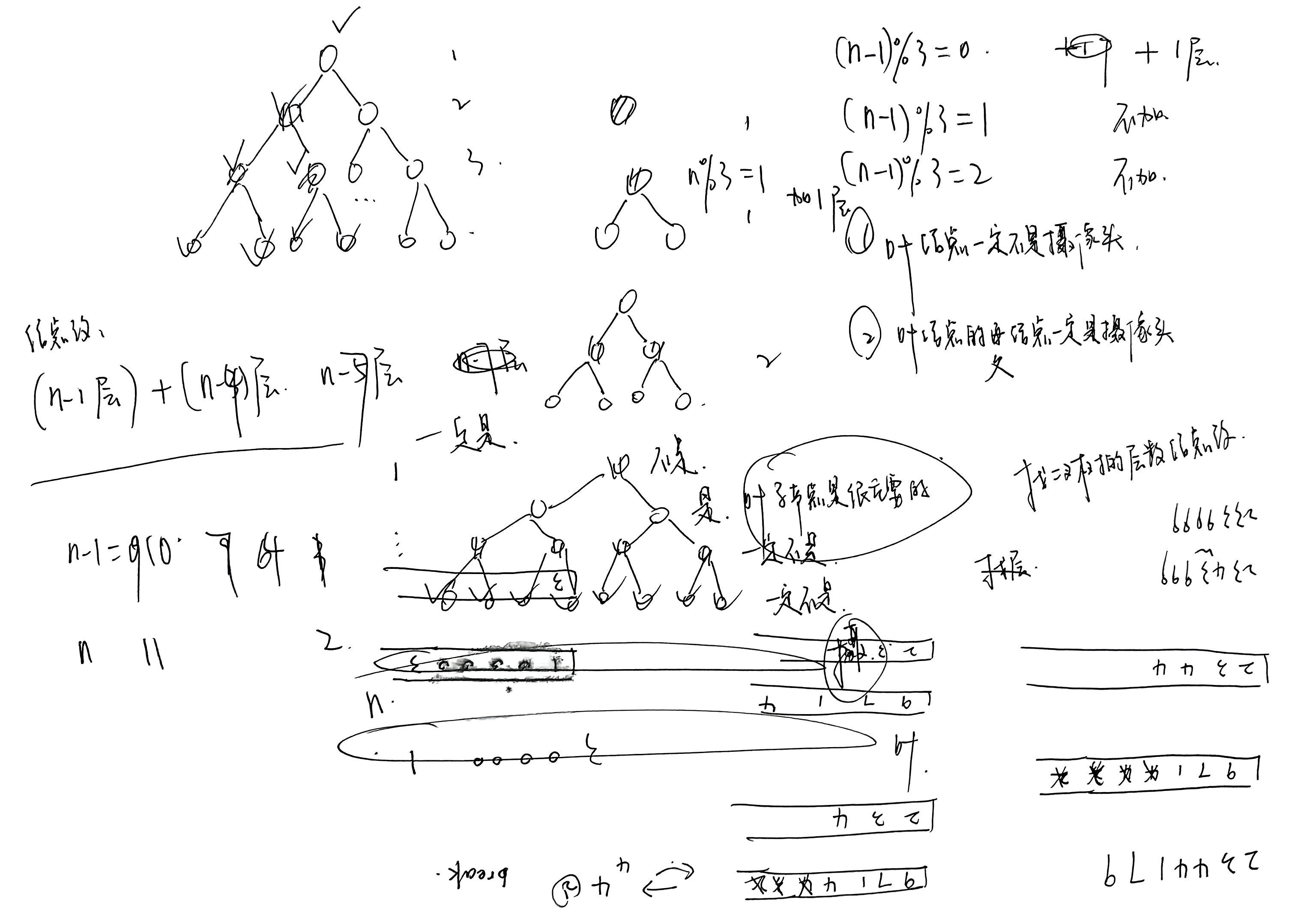
当我理解完Carl的题解之后，我觉得我自己要独立做出这道hard，思路上还需要理解以下点（由浅至深）：

1. 考虑单位。任意的二叉树一定就不能够以层为算法单位，因为你没办法保证每一个子树的叶结点落在哪里，所以一定是一个结点为基本单位。
2. 遍历顺序。从上至下，所以采用后序遍历。
3. 状态标签化。将结点的状态划分类别并将其标签化。
4. 状态转移（静态的）（此处的转移指的是结点之间的依赖关系）。考虑单位是一个个结点，并且自底向上遍历-->父结点的状态由子节点决定。
5. 边界控制。递归的结束条件一定是落到空结点上，而根据“叶结点一定为无覆盖状态”去推得赋予空结点的状态也是很巧妙的。将边界纳入到算法统一考虑的范围内。最后再通过对根结点本身的状态查询来决定是否需要在根结点上加装一个摄像头。

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int traversal(TreeNode* root, int& ans){
        if(root == nullptr) return 2;
        int left = traversal(root->left, ans);
        int right = traversal(root->right, ans);

        if(left == 3 || right == 3){
            ans++;
            return 1;
        }
        else if(left == 1 || right == 1) return 2;
        else if(left == 2 && right == 2) return 3;

        else return 0;
        return 0;
    }

    int minCameraCover(TreeNode* root) {
        int ans = 0;
        if(traversal(root, ans) == 3) ans++;
        return ans;
    }
};