Coding | [代码随想录][动态规划] 377.组合总和Ⅳ —— 爬楼梯是对的

题面

给你一个由不同整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

链接：Leetcode 377.组合总和Ⅳ

思路

首先，逆天题目把组合称为顺序不同的序列。

因为代码随想录顺序的原因，我顺理成章地把它和之前的零钱兑换Ⅱ一块儿思考——从组合数到排列数我需要怎么构造递推公式？dp数组的格式是什么样的？下标的含义是什么？再加上Carl说这道题的递推公式和零钱兑换Ⅱ并无差别，而我在解零钱兑换的时候根本没有参考Carl的压缩版解法，而是采用二维dp数组，我便一直在追求如何用二维数组和原来的递推公式求解。

后来发现零钱兑换Ⅱ的二维dp数组解法的递推公式根本不适用。

危急关头，我幸而在题解中瞄到了这样一个解法：

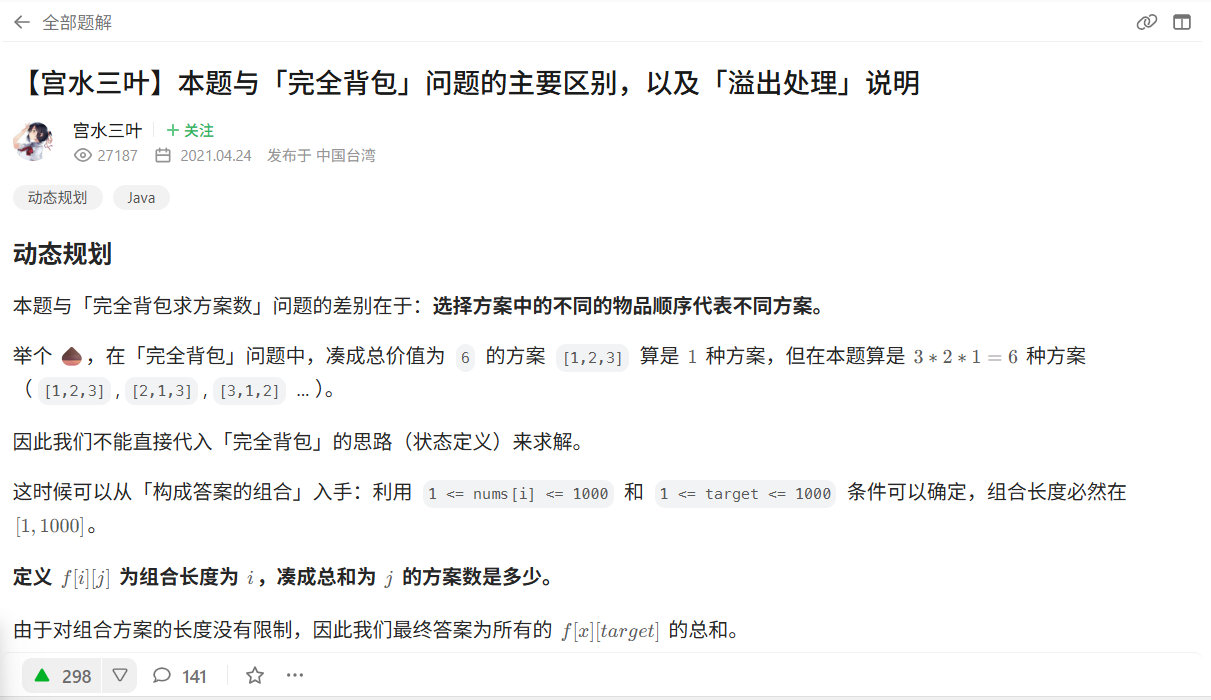
其提出的转移方程让我豁然开朗。

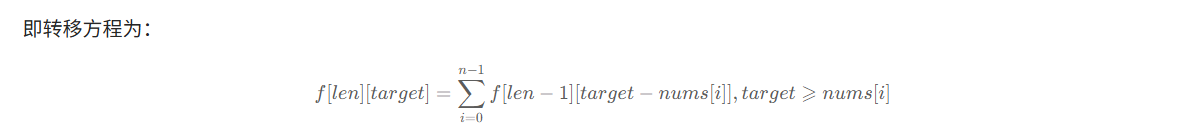
将i的含义从“只考虑前i个数”变为“只考虑i个数”，这样就能避开前者带来的组合数问题，又能得到一个递推公式。dp含义和递推公式的确定之后，编码也很简单了。

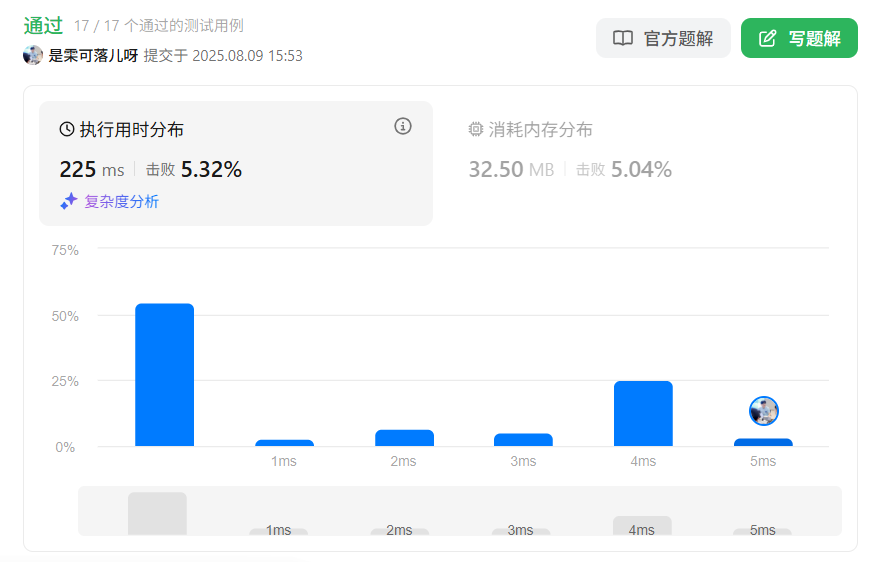
但是当我回头看代码随想录的题解，在心中模拟这个一维数组的时候……

这不就是爬楼梯吗？

dp[j] += dp[j - nums[i]]。

最后一个数采取i = 最后一个台阶用i步上的。那么这一情况下的方案数量即为任何方式到达j - nums[i]的方案数量。

随后通过这一个逻辑，时间和空间上都得到了优化。

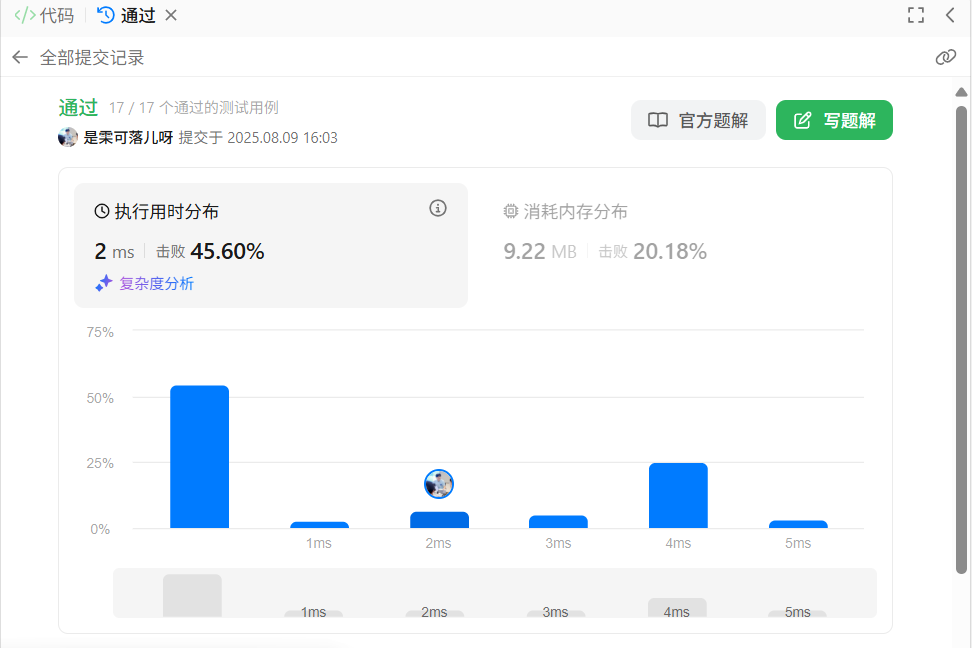
说实话，我并不是说Carl题的顺序安排得有问题，这也很好的提醒了我，若是不按照Carl安排好的题目顺序刷题，我还能在看到这道题的时候就想到用什么方法吗？但是Carl讲这道题确实讲的复杂了，这就是一道爬楼梯和斐波拉契数的问题，完全不用和组合数扯到一块儿。

话又说回来，我想到Carl在某个视频中提到：上台阶有m种方案，m不定。这个问题是完全背包问题。在学习之后我又在怀疑，难道原本的上台阶不是完全背包问题吗？他也允许重复采用一个上台阶的步数啊……

Whatever，想通了总是很爽的。

题解

代码1：二维数组

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<vector<unsigned long long>> dp(target + 1, vector<unsigned long long>(target + 1, 0));
        for(int j = 0; j < dp[0].size(); j++){
            if(j == 0) dp[0][j] = 1;
            else dp[0][j] = 0;
        }

        for(int i = 1; i < dp.size(); i++){
            dp[i][0] = 0;
        }

        for(int i = 1; i < dp.size(); i++){
            for(int j = 1; j < dp[0].size(); j++){
                int total = 0;
                for(int m: nums){
                    if(j >= m) total += dp[i - 1][j - m];
                    else continue;
                }
                dp[i][j] = total;
            }
        }

        int result = 0;
        for(int i = 0; i < dp.size(); i++){
            result += dp[i][target];
        }
        return result;
    }
};

代码2：一维数组爬楼梯

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<unsigned long long> dp(target + 1);

        dp[0] = 1;
        for(int j = 0; j <= target; j++){
            for(int i = 0; i < nums.size(); i++){
                if(j >= nums[i]) dp[j] += dp[j - nums[i]];
                else continue;
            }
        }

        return dp[target];
    }
};