笔记下载
链接:https://pan.baidu.com/s/1bFz8IX6EkFMWTfY9ozvVpg?pwd=deng
提取码:deng
b站视频:408-计算机网络-笔记分享_哔哩哔哩_bilibili
包含了408四门科目(数据结构、操作系统、计算机组成原理、计算机网络)
如果链接失效了,看看b站,或者私信我
408相关资料(真题 模拟卷等)
链接: https://pan.baidu.com/s/1Qga8aMgcrVfCmrry68vqog?pwd=974t提取码: 974t
🌸章节汇总
目录
二、第二章——数据的表示和运算
1、进位制度(二进制、十进制)
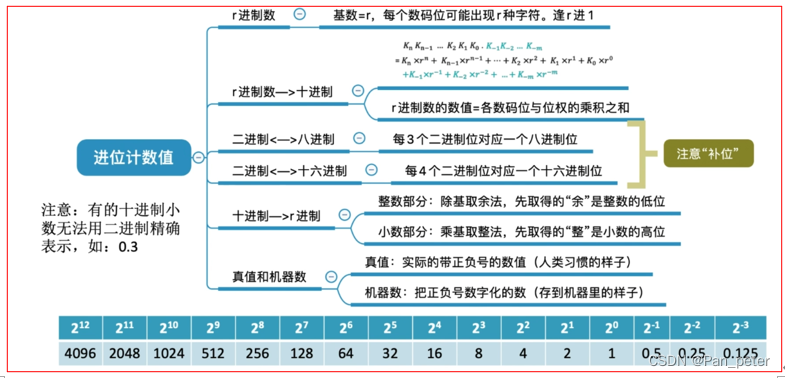
2、BCD码(余三码、2421码)

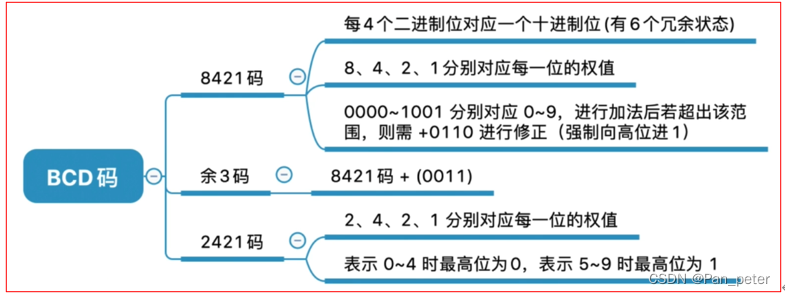
| 编码方式 | 功能 | 好处 | 弊处 |
| BCD码 | 将每个十进制数码转换为4位二进制码 | 精度高,适合直接用于数码管或LED等显示设备 | 编码长度长,占用存储空间多,运算速度慢 |
| 余三码 | 将每个十进制数码转换为3位二进制码 | 编码长度相对BCD码较短,占用存储空间相对较小 | 运算复杂,不易实现,精度较低 |
| 2421码 | 将每个十进制数码分别转换为2位、4位、2位和1位二进制码 | 编码长度短,可减少存储空间的占用 | 运算复杂,不易实现,精度较低 |
3、原码、反码、补码
无论是加法还是减法,都会把数值转为二进制补码进行运算
补码——(符号位)参与运算 !!!——
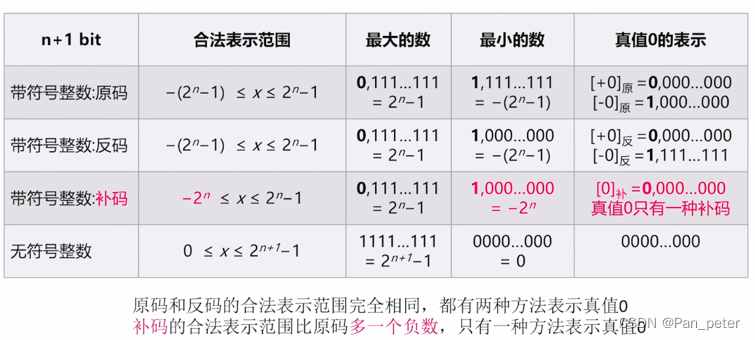
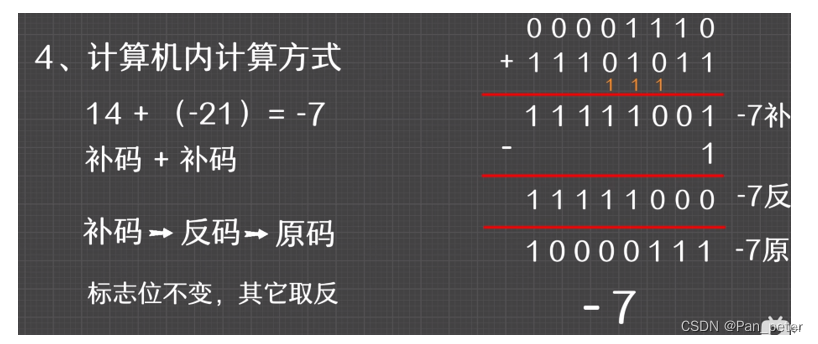
3、定点小数
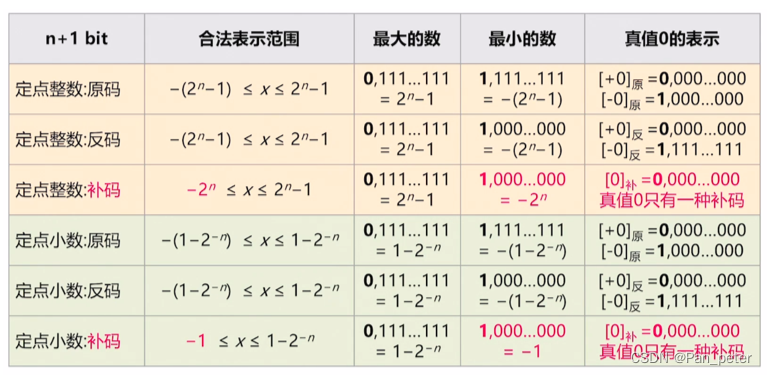
原码表示范围为1.111 1111 ~0.111 1111,即-127/128到127/128
反码表示范围为1.000 0000~0.111 1111,即-127/128到127/128
补码表示范围为1.000 0000~0.111 1111,即-1到127/128
为什么是最小-1,因为这是小数啊!小数就是-1 ~
(1.0000000)原码= (1.0000000)反码 = (1.0000000) 补码 = -1
-1.0的原码通过纯小数的原码表示公式却表示不了,
我们无法得到-1.0的原码
但我们可以通过纯小数的补码表示公式得到-1.0的补码:
[-1.0]补=2+(-1.0)=1.000 0000
3、效验(奇偶校验码——看1)
不足:
只能检测奇数个错误!!!(如果有—偶数个错误位—那么将检测不出来)
只能用来检错,不能纠错!!!
好处:
电路实现简单——使用异或电路——就可以判断出1的个数
 1的总数为偶数—— 异或得到的结果为 0(可以从异或表中看出结果,当为0异或1时,为1)
1的总数为偶数—— 异或得到的结果为 0(可以从异或表中看出结果,当为0异或1时,为1)
4、算术逻辑单元(ALU)
(1)一位全加器(FA – full adder)
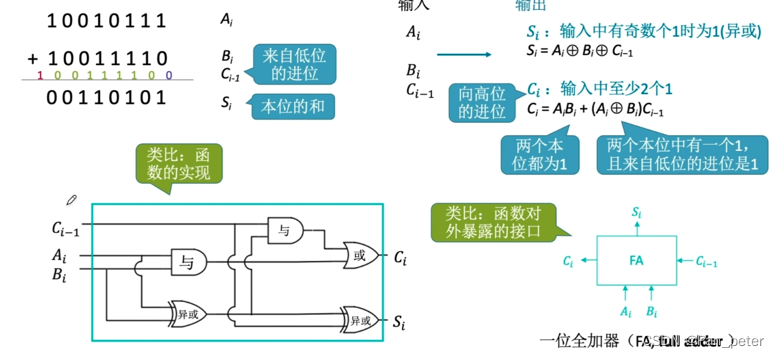
输入: 两个数(0 / 1),低位的进位
输出: 进位信号,输出数(0 / 1)
用了2个与门,2个异或门,1个或门
封装:n个1位全加器,就可以构成n位加法器(串行加法器)——封装好,直接输入数据,就可以获得对应的结果——函数思想 —— 避免重复造轮子 (了解思想 – 自行优化 – 改造 !!!)
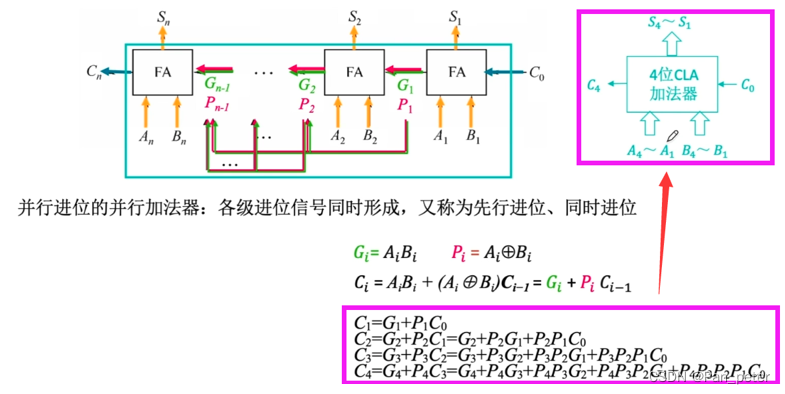
(2)并行加法器
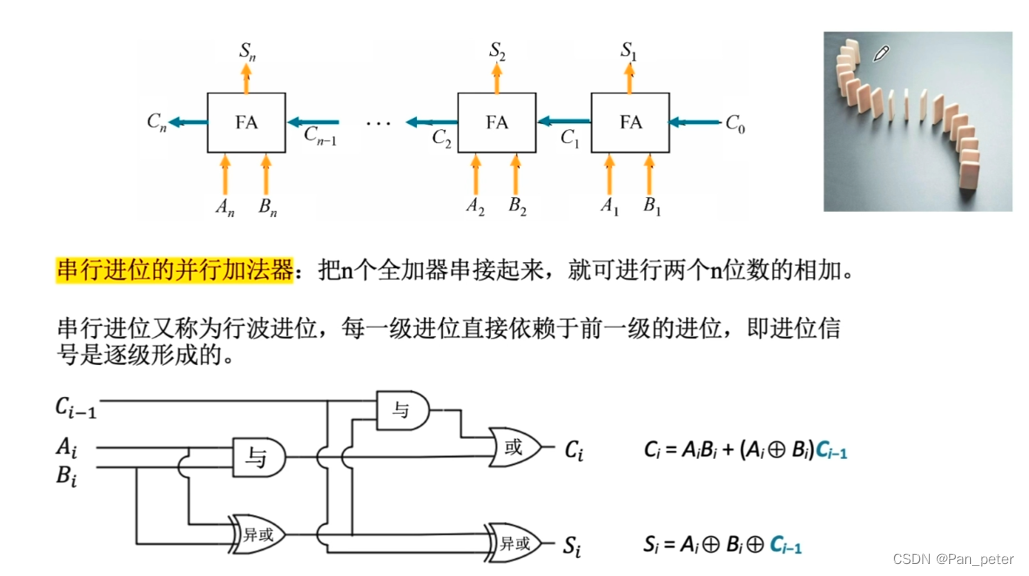
(3)总结
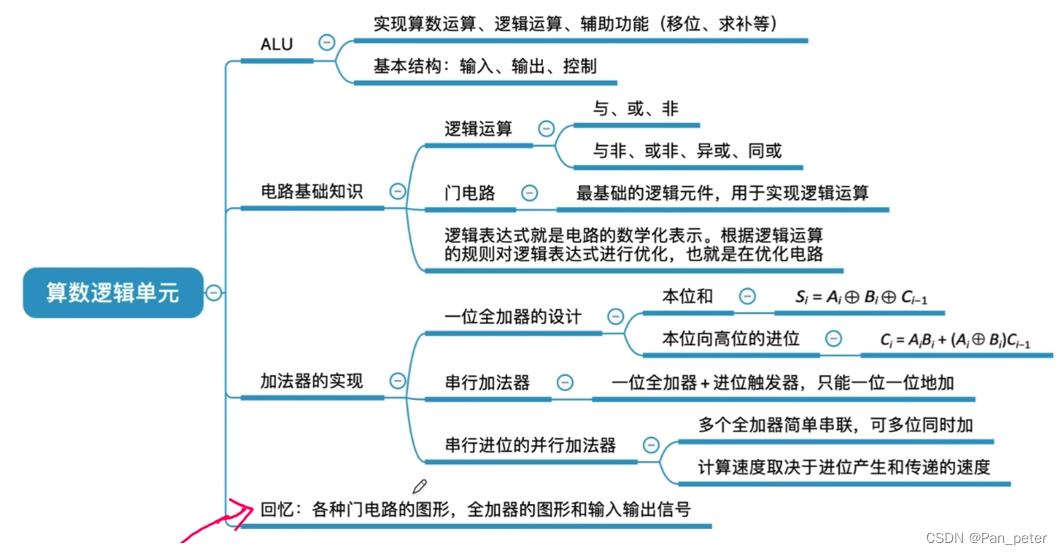
(4)并行加法器(plus)
优点: 并行执行,几乎同时出结果(毕竟硬件的速度-超乎你想象)
缺点: 位数越多——硬件电路越复杂!! —— 成本高
优化: 4位 + 4位 (不往上叠加)
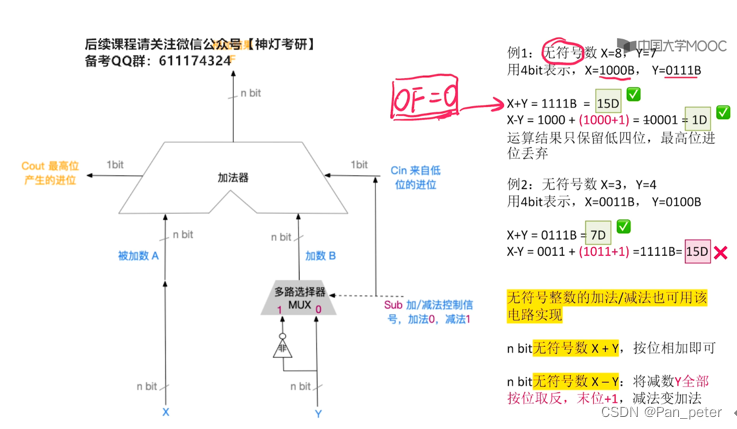
(5)补码加减运算器(含-标志位)
加减法——适用于——无符号 + 有符合 (都适用 !!!)

初级(会溢出——有问题!!!)
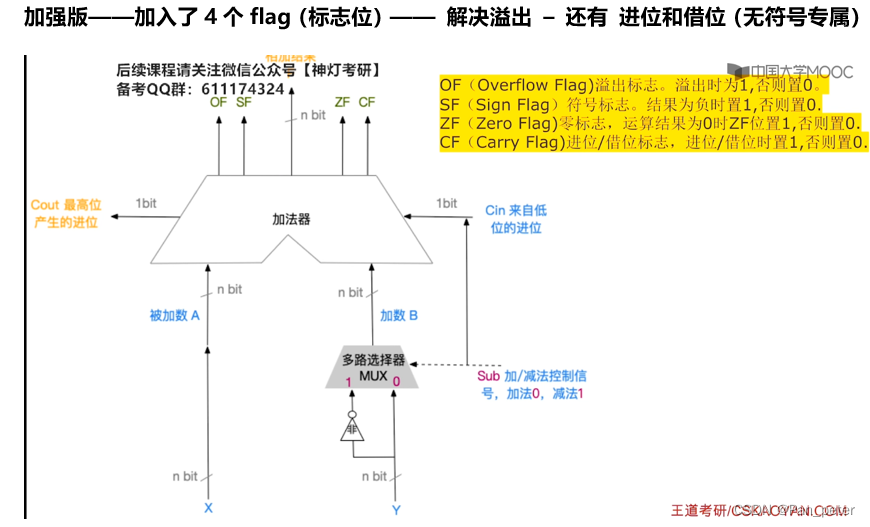
加强版——加入了4个flag(标志位)—— 解决溢出 – 还有 进位和借位(无符号专属)
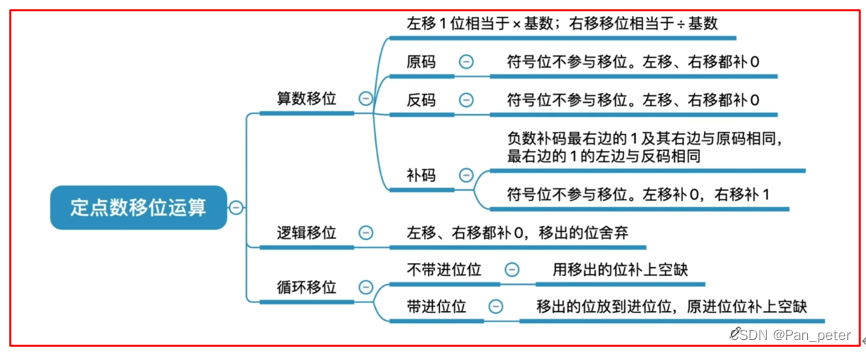
5、定点数的移位运算(讲的略简单)
6、原码——乘法
(1)一位乘法
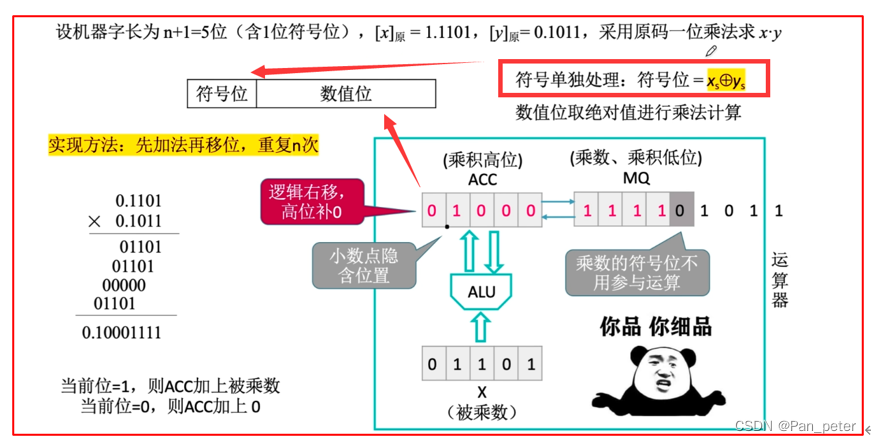
(1)手算(小数和整数——类似)

7、原码——除法
恢复余数法
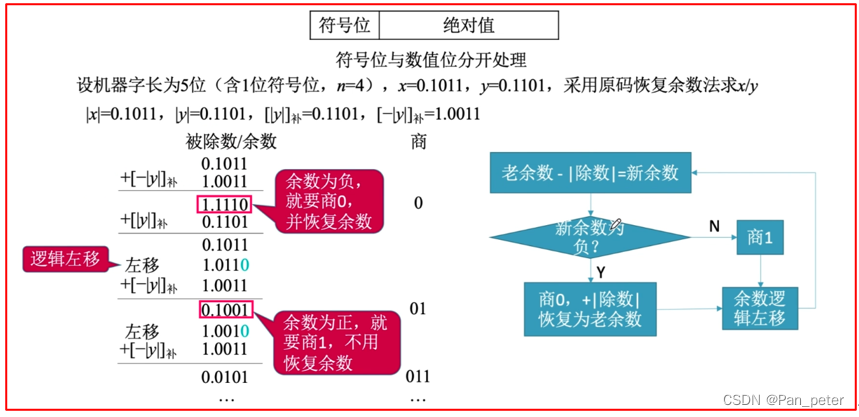
改良——因为当你为负数时!那么必然左移之后就可以被除!!!
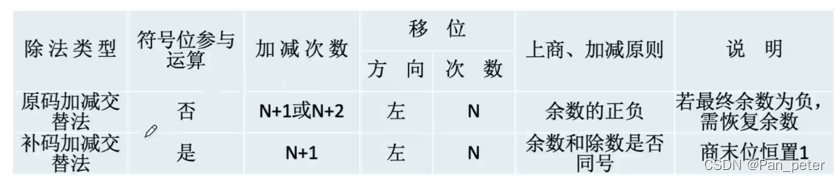
加减交替法(不恢复余数法—but:最后一步需要恢复)

注意:
(左移)要比(加减次数)少一次!
(加减次数)的总次数:(n+1) || (n+2)
(除数)一定要小于(被除数)——如果不是,则会在第一步中被终止!
(因为被除数减除数 小于 0)
(因此——定点小数除法——无法表示除数比被除数大的计算!!!)
8、补码——除法
更正:除数为11.0101
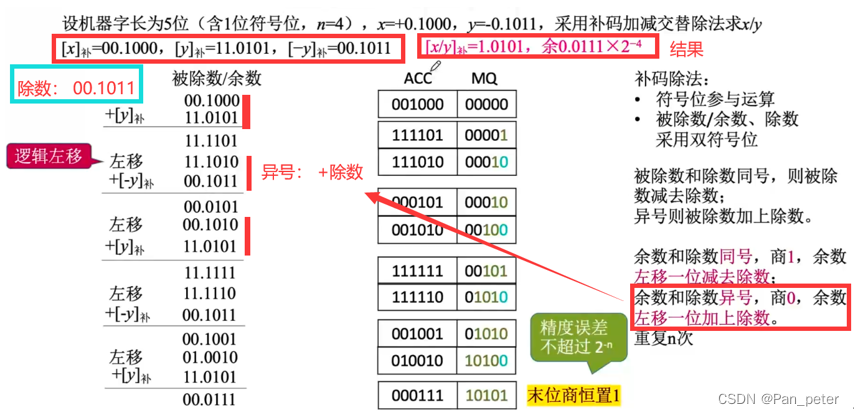
9、数据的存储与排列(大端 & 小端)
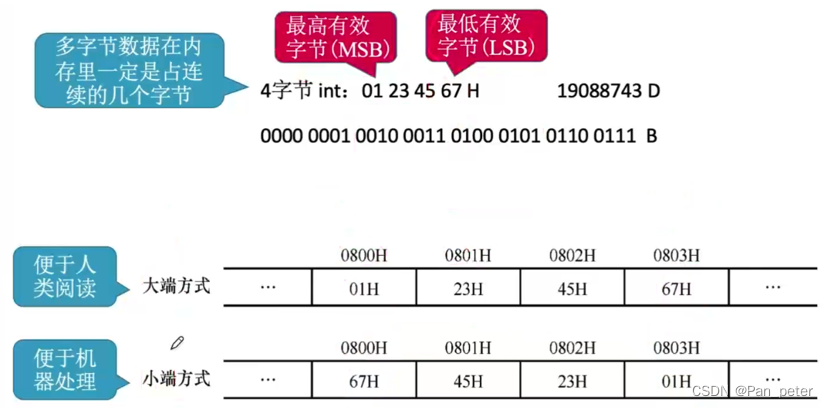
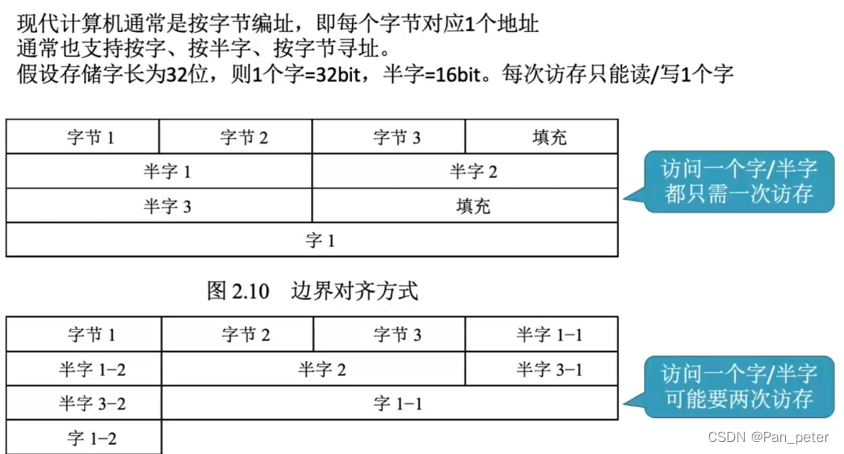
(1)边界对齐(时间 – 空间 – 字节转换)
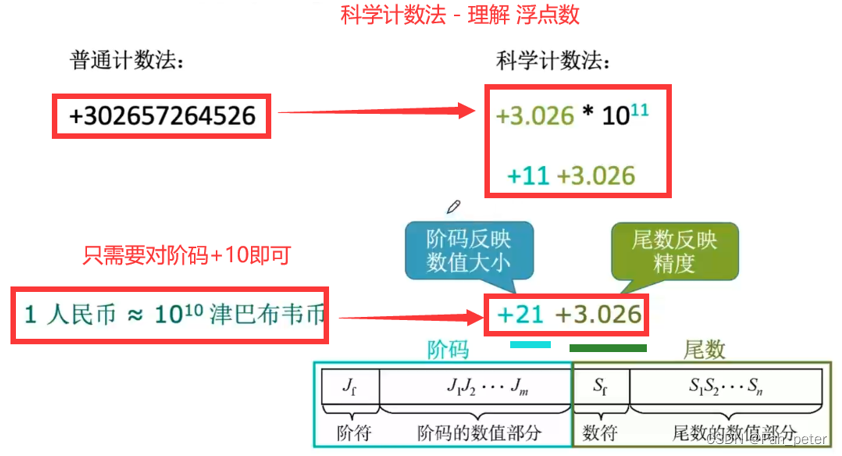
10、浮点数表示(重难点※※※※※)
科学计数法——表示
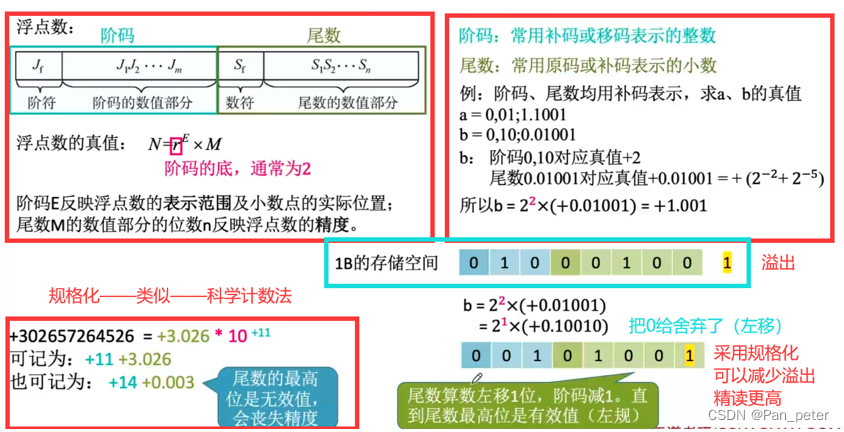
浮点数——表示方法

(1)规格化
2^5 : 304.231 —— 右规 —— 2^7 : 3.042 (小数点不动——尾数右移)
2^5 : 0.00123 —— 左规 —— 2^3 : 0.123 (小数点不动——尾数左移)
好处——增加了精读(避免了无效的0占位置)
弊处——需要改变阶码的数——万一超出了阶码的表示范围呢????
巧妙点:用了双符号位——来防止溢出

不考的点——规格化——有数不能表示——表示
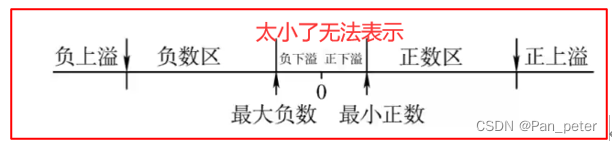
(2)规格化特点

上面写错了:左移三位后——应该是: 1.0100 000
(3)总结
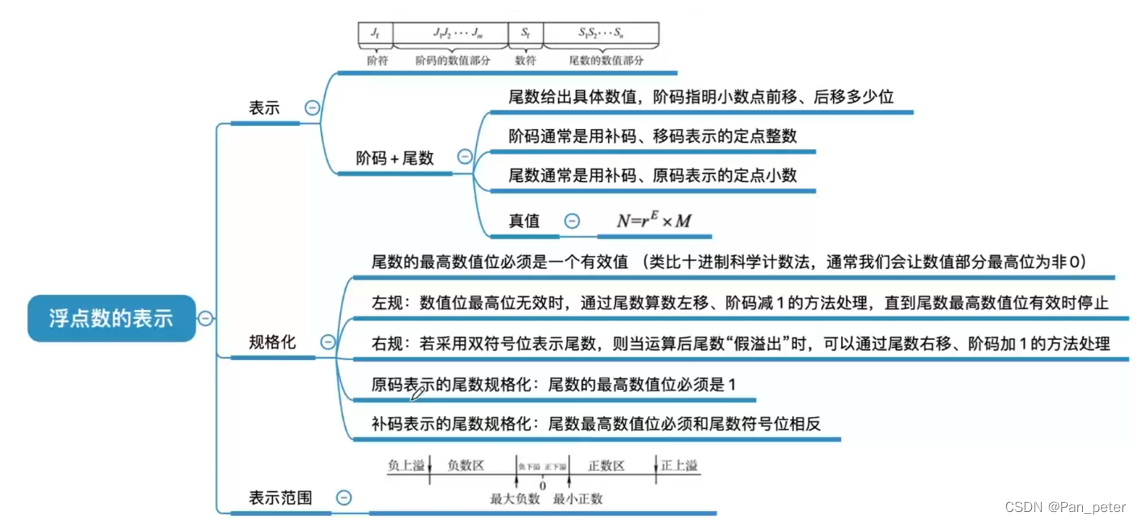
11、IEEE(I triple E)

(1)移码
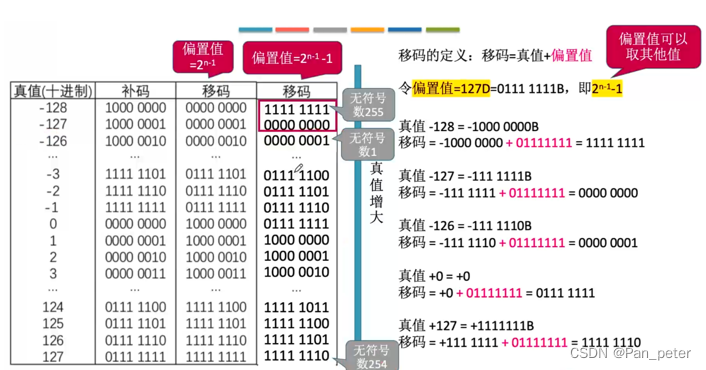
(2)重点(表示范围、转换)
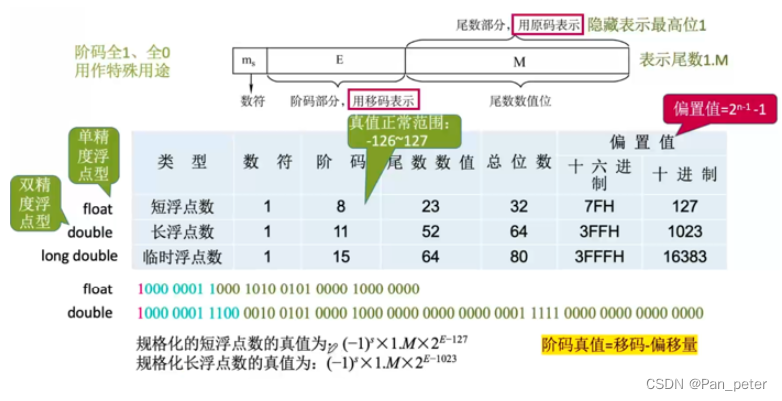
注意:
阶码——全0、全1有特殊用途
真值 = 移码 – 偏移量
二进制数(机器中展示的) —— 十进制数 —— 两者的相互转换!!!


12、浮点数的运算
(1)十进制

(2)二进制计算

(3)【0舍1入法】与【恒置1法】

(4)强制类型转换
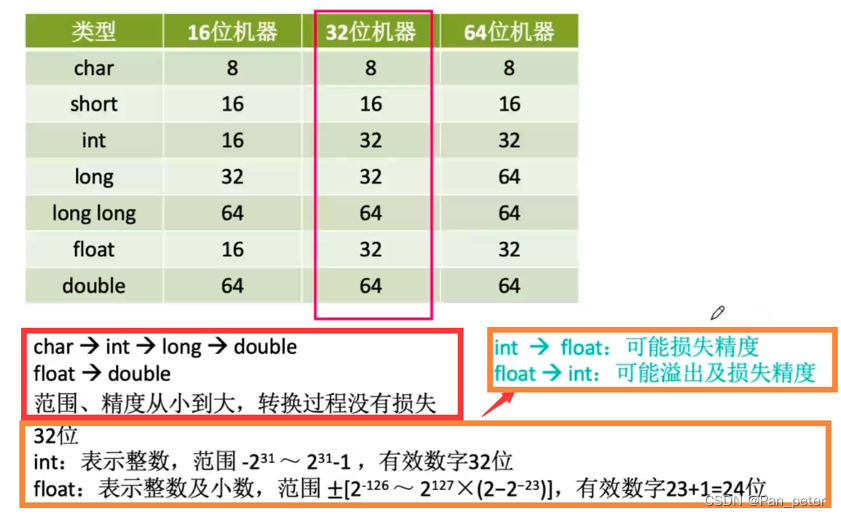
注意:
什么时候会有:精读丢失、溢出
(5)小结
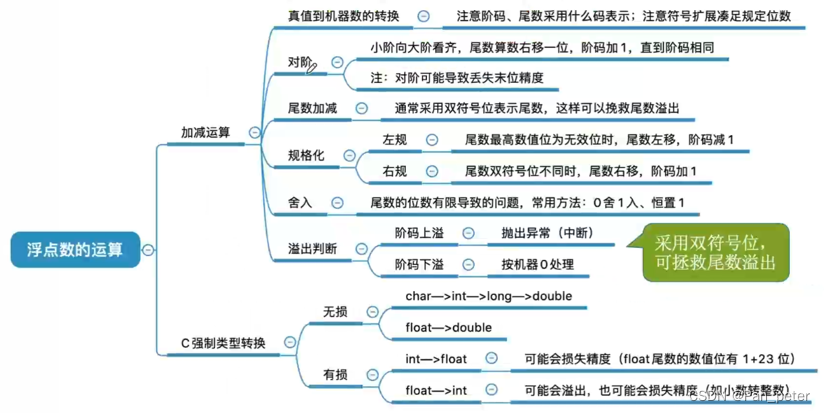





 本文详细介绍了计算机系统中的数据表示与运算,包括进位制度、BCD码、原码、反码、补码、定点数和浮点数的表示方法,以及算术逻辑单元、移位运算、浮点数运算规则等,重点讲解了IEEE标准在浮点数表示中的应用。
本文详细介绍了计算机系统中的数据表示与运算,包括进位制度、BCD码、原码、反码、补码、定点数和浮点数的表示方法,以及算术逻辑单元、移位运算、浮点数运算规则等,重点讲解了IEEE标准在浮点数表示中的应用。

















 2977
2977

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










