树状数组详解（简单超基础超详细c++）

什么是树状数组
树状数组是 一 个查询和修改复杂度都为 log(n) 的数据结构。主要用于： 数组的单点修 改 、 区 间 求 和。
在使用前缀和求区间和的算法中，如果可以做到在0(1)的时间复杂度内查询任意的区 间和，但是如果要修改其中 一个点的值，那么需要修改 一遍前缀和数组，修改的时间复杂度 是 0(n)。
(1)树状数组拆分原理
正如所有的整数都可以表示成2 的幂和，我们也可以把 一 串序列表示成 一 系列子序列 的和。采用这个想法，我们可将 一 个前缀和划分成多个子序列的和，而划分的方法与数的2 的幂和具有极其相似的方式。
比如：整数21的对应的2进制是10101,对应计算=2⁴+2²+21,因此一个长度
为21的数组，可以拆分为三段：

子序列的个数是其二进制表示中1的个数。
根据该理论， 一 个长度为len 的 区 间 [ 1 ,len], 可以采用上述思想划分为log(len) 个 子 区 间 。
从右向左看，每个区间的大小其实是len 对应二进制的最后一个1的2的次幂。

(2)如何求整数x 对应二进制的最后一个1往后的值?
lowbit(x): 代表x 对应2进制的从最后一位1开始向后构成的值。
例如 ：
lowbit(10): 返 回 1 0 。
lowbit(40): 返 回 1000。
计算方法 ：
假设x=270 对应的2进制为：1011,1000。
先将x 取反 = 0100,0111, 再+1 = 0100,1000,此时发现这个值和原来的x 对应的 2进制，最后一个1向后的值一致，前面的值正好相反，只要拿这两个值做&运算，结果就 是lowbit(x) 的值。
在计算机中，负数是以补码的形式存储的，补码就是数值位取反+1的过程。
因此：lowbit(x)=x&(~x+1)=x &-x;

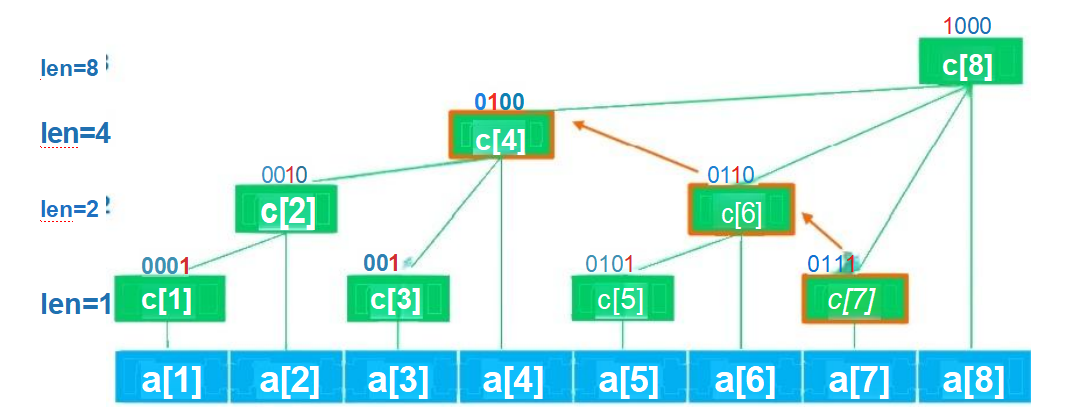
(3)树状数组的划分方法
以 a[x] 结尾的区间，区间长度为x 的 最 后 一 个 1所 对 应 的 2 的 次 幂 。

A. 以 a[x] 结尾的区间，区间长度为x 的最后一个1所对应的2的次幂。
B. 设定 c[x] 表示：a 数组中，长度为 lowbit(x) 的区间和，所管理的区间为[x-
lowbit(x)+1,x]。
C. 该结构的特点：
a. 除树根外，结点x 的 父 结 点 = x+lowbit(x);
b. 长度为n 的数组 a, 所构建的树的深度= log(n);
注意：树状数组的下标一般从1开始，因为如果从0开始， lowbit(0)=0, 容易出 现死循环。

(4)树状数组修改元素
`
代码示例：

//在数组a的第x数上增加数字k
void_update(int x,int k){
	for(int i=x;i<=n;i=i+lowbit(i)) c[×]+=k;
}

(5)树状数组求前缀和

//求[1,x]的前缀和
int qurrey(int x){
	int res=0;
	for(int i=x;i>=1;i-=lowbit(i)){
		res+=c[i];
	}
	return res;
}

典型例题助理解：

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int c[N];
int n,m; 

//求二进制后缀一的值
int lowbit(int x){
	return x&(-x);
}

//在数组的x位置加上p
void add(int x,int p){
	for(int i=x;i<=n;i+=lowbit(i)){
		c[i]+=p;
	}
}

//求和数组[1,x]的和
int qurrey(int x){
	int res=0;
	for(int i=x;i>=1;i-=lowbit(i)){
		res+=c[i];
	}
	return res;
}
int main(){
	scanf("%d%d",&n,&m);
	
	int x;
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		add(i,x);
	}
	
	int y,z;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&x,&y,&z);
		if(x==0){
			printf("%d\n",qurrey(z)-qurrey(y-1));//数组[y,z]的和
		}else if(x==1){
			add(y,z);
		}
	}

    return 0;
}