[Machine Learning] 分类（Classification）

Keywords

• Classification（分类）
• Generative Model（生成模型）
• Gaussian Distribution（高斯分布）
• Maximum Likelihood（极大似然估计）

Classification（分类）

• Input:目标 x
• Output:这个目标x属于n个Class中的哪个Class

Classification的应用

• Credit Scoring（信用评分）

  • Input：income（收入）, savings（存款）, profession（职业）, age（年龄）, past financial history（金融记录） …
  • Output：accept or refuce（接受或者拒绝贷款）

• Medical Diagnosis（医疗诊断）

  • Input：current symptoms（当前症状）, age（年龄）, gender（性别）, past medical history（医疗记录） …
  • Output：which kind of diseases（哪种类型的疾病）

• Handwritten character recognition（手写文字辨识）

  • Input：手写字体
  • Output：字体库中的哪个字

• Face recognition（人脸识别）

  • Input：image of a face（脸部图像）
  • Output：person（人）

Example Application（应用举例）

• Input：某一只Pokemon精灵（数值化，一只Pokemon由以下七个数值表示）
  • Total：总体强度
  • HP：生命值
  • Attack：攻击力
  • Defence：防御力
  • SP Atk：特殊攻击力
  • SP Def：特殊防御力
  • Speed：速度
• Output：这一只Pokemon精灵所属系
  • 皮卡丘——雷
  • 杰尼龟——水
  • 妙蛙草——草

How to do Classification（如何做分类）

• Training data for Calssification（分类所需的训练数据）

  将已经收集的Pokemon精灵转化为元组训练数据（如下图）

• Classification as Regression（用Regression的方法进行分类）

  可能这时候你会想，我们可不可以用之前学过的《[Machine Learning] Regression（回归）》的方法来进行Classification（分类）呢？

  假设我们现在只需要将Pokemon精灵分成两类，那么：

  • 训练过程：将Class 1代表$\hat{y}=1$，Class 2代表$\hat{y}=2$的数据作为训练数据，然后对Model进行训练
  • 测试过程：将测试数据代入训练好的Model，将最终Model输出值以0为分界点，Model输出值接近1即为Class 1，Model输出值接近-1即为Class 2

  如果这样做我们会遇到什么问题呢？下面我们来探究一下！

  

  如上图所示，假设我们现在的Model为$y=b+{\omega }_1{x}_1+{\omega }_2{x}_2$，蓝色点为Class 1（$\hat{y}=1$），红色点为Class 2（$\hat{y}=-1$），那么我们最终可以训练出一个类似图中绿色线（$b+{\omega }_1{x}_1+{\omega }_2{x}_2=0$）的Model，Model输出值接近1（比如0.98）的点在线的一边，而Model输出值接近-1（比如-0.52）的点在线的另一边，这显然是个不错的结果。

  但是！如果现在我们的训练数据像下图一样分布，然而我们依旧用Regression（回归）的方法的话，那么结果并不会这么完美。

  可以发现，图中多出了一些蓝色点Class 1（$\hat{y}=1$）的训练数据，它们距离绿色线（$b+{\omega }_1{x}_1+{\omega }_2{x}_2=0$）很远，即$b+{\omega }_1{x}_1+{\omega }_2{x}_2>>1$，那么在训练过程中，机器就会认为它们是错误的点，因为这些点并不接近1，而是远大于1，这会使得Loss Funtion（损失函数）很大。

  所以在用Model为$y=b+{\omega }_1{x}_1+{\omega }_2{x}_2$做Regularization（回归）的时候，最终的Model并不会得到向绿色那样的线，而是会向下倾斜，类似紫色线，机器认为这样的好处就是让那些远大于1的点接近1，使得Loss Funtion（损失函数）变小。

  

  显然，现在出现了一种情况，对于Regularization（回归来说），紫色的线是一个好的Function；但是对于Classification（分类）来说，绿色的线才是一个好的Function。因此，用Regularization（回归）的方法来做Classification（分类）并不是一个好的办法！

  现在还有一个问题！就是在做多分类问题的时候，训练数据会出现一种情况：将Class 1代表$\hat{y}=1$，Class 2代表$\hat{y}=2$，Class 3代表$\hat{y}=3$…其实这样做是有问题的。机器会认为，Class 1和Class2接近，因此会有某种关系，Class 2和Class3接近，一次你又会有某种关系…但是，如果实际上这些关系并不存在的话，那么最终训练出来的模型会是一个糟糕的模型！

  那我们应该怎么做呢？

Generative Model（生成模型）

Two Box

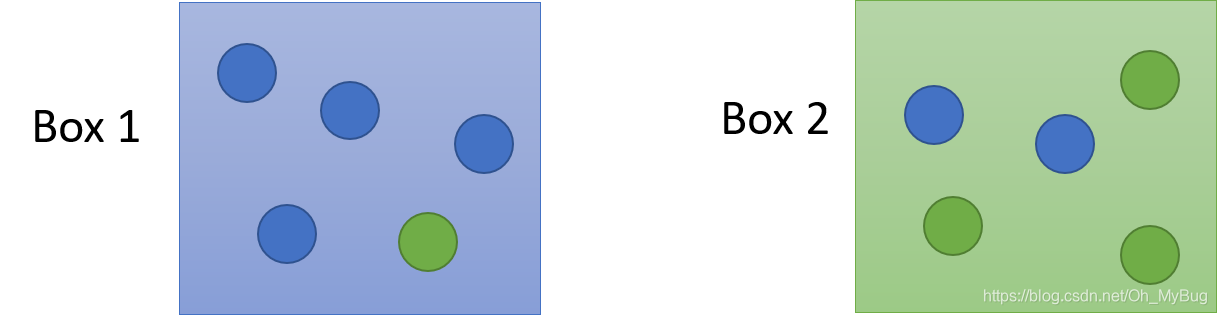
首先我们来看两个一模一样的盒子（Box 1 & Box 2），盒子里面放有蓝球和绿球，现在已知：

• 从Box 1中抽出一个球的概率$P(B_1)=\frac{2}{3}$
• 从Box 2中抽出一个球的概率$P(B_2)=\frac{1}{3}$
• 在Box 1里，蓝球占$P(Blue|B_1)=\frac{4}{5}P(Green|B_1)=\frac{1}{5}$
• 在Box 2里，蓝球占$P(Blue|B_2)=\frac{2}{5}P(Green|B_2)=\frac{3}{5}$

现在让你求一个蓝球在Box 1中抽中的概率，即$P(B_1|Blue)$，学过概率论与数理统计的都知道全概率公式（具体可看《[Machine Learning] 贝叶斯公式 & 全概率公式（Bayes Rule & Total Probability Theorem）》）：

$$P(B_1|Blue)=\frac{P(Blue|B_1)P(B_1)}{P(Blue|B_1)P(B_1)+P(Blue|B_2)P(B_2)}$$

那这个跟Classification（分类）有什么关系呢？我们再来看一下！

Two Class

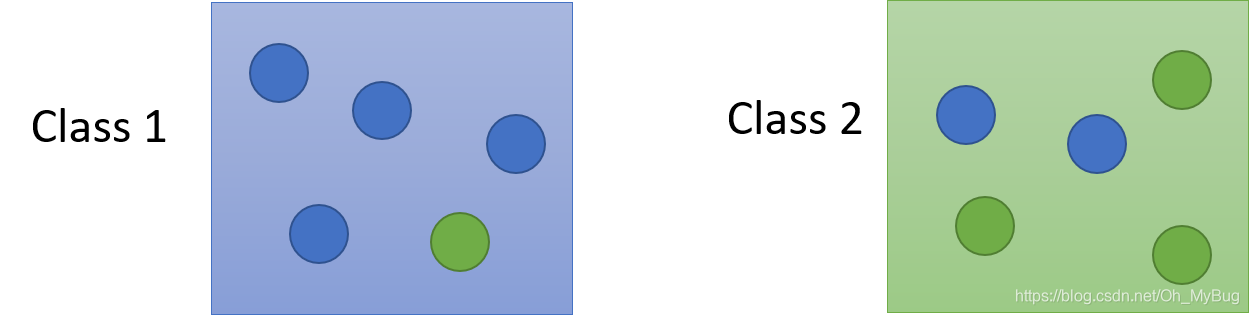
我们把Box换成Class，里面装了两种不同系的Pokemon精灵。现在已知一个Pokemon精灵$x$，问这个Pokemon精灵$x$在某一个Class中的几率各自是多少呢？

这时候我们就需要知道以下条件：

• 从Class 1抽出一个Pokemon精灵的概率$P(C_1)$
• 从Class 2抽出一个Pokemon精灵的概率$P(C_2)$
• 在Class 1中，抽出（Sample）是$x$的概率$P(x|C_1)$
• 在Class 2中，抽出（Sample）是$x$的概率$P(x|C_2)$

有了这些条件，我们就可以确定Pokemon精灵$x$来自Class 1的概率：

$$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$$

知道了这些，我们就可以比较一只Pokemon精灵，它来自Class 1和来自Class 2的概率哪个更大，概率最大的那个就是正确答案！

所以如果我们考虑二元分类的话，我们现在需要算的就是那四个值$P(C_1)$、$P(C_2)$、$P(x|C_1)$、$P(x|C_2)$

那怎么知道这些值呢？我们就希望从Training Data中去把这些值估测出来。这种方法就是Generative Model（生成模型）。

有了Generative Model（生成模型），我们就可以计算某个$x$出现的概率:
$$P(x)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2)$$

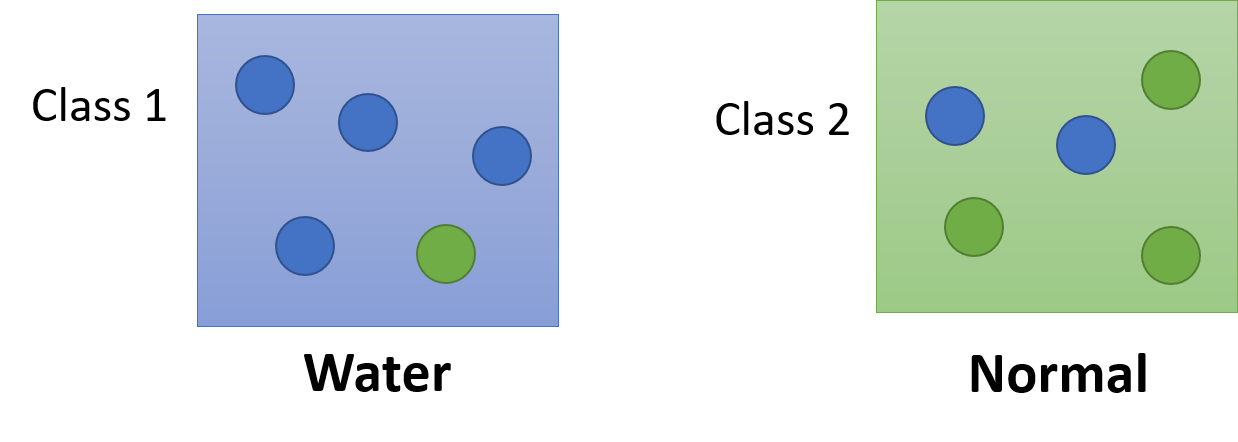
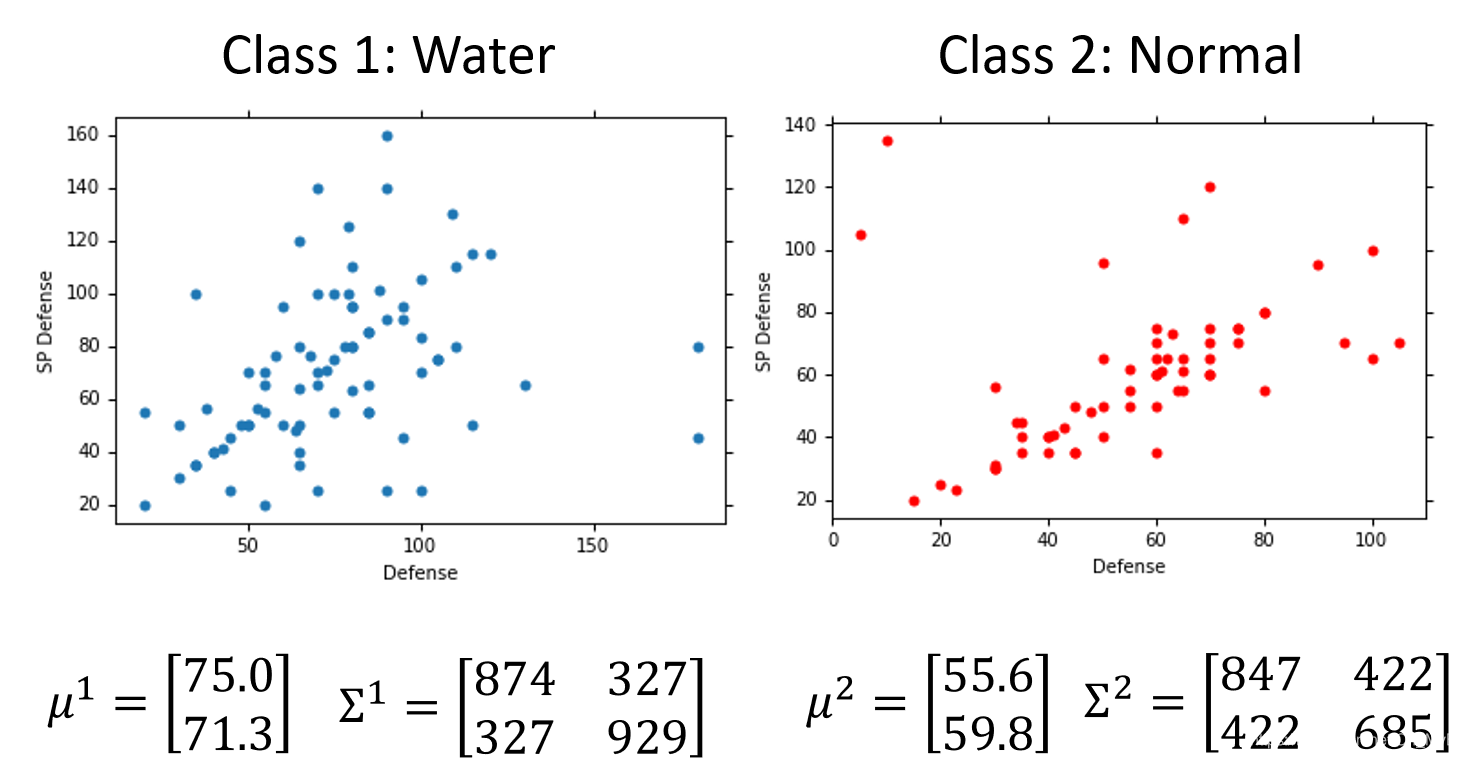
现在假设Class 1为Water（水）系，Class 2为Normal（一般）系，在Training Data（训练集）中：由79只Pokemon精灵为Water（水）系还有61只Pokemon精灵为Normal（一般）系。则：

• $P(C_1)=79/(79+61)=0.56$
• $P(C_2)=61/(79+61)=0.44$

那我们现在怎么计算一只未知的Pokemon精灵$x$分别来自在Class 1和Class 2中的概率呢？

Probability from class

我们知道，每一个Pokemon精灵都被一个向量所表示，而向量中的值就是Pokemon精灵的特征值（feature）。

为了可视化，我们暂时先考虑两个特征值：Defence（防御力）和SP Defence（特殊防御力）。

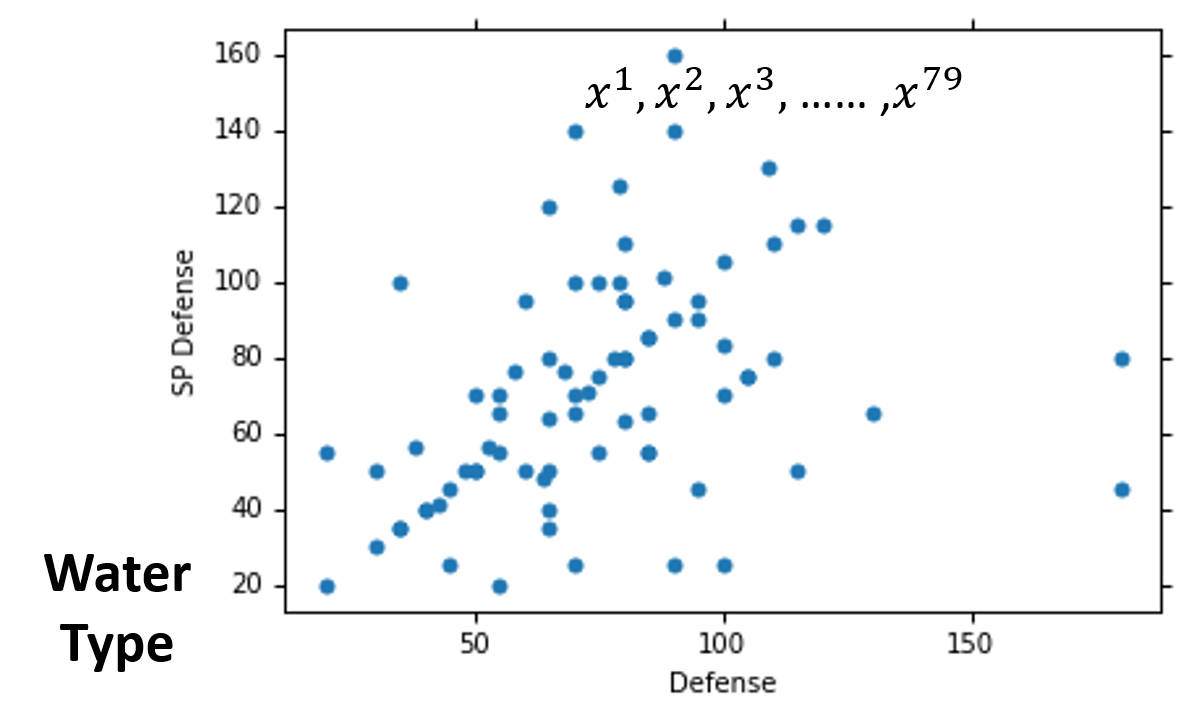
首先，我们将79只Water（水）系精灵的Defence（防御力）和SP Defence（特殊防御力）可视化（如上图）。所以图中每一个点都代表了一只Water（水）系Pokemon精灵。

现在，出现了一只未知系的Pokemon精灵$x$，我们要想办法估测出这只Pokemon精灵$x$是Water（水）系的概率。

我们可以假设Water（水）系Pokemon精灵的概率分布满足Gaussian Distribution（高斯分布），而这79只Water（水）系精灵就是为了让我们算出这个Gaussian Distribution（高斯分布）的具体公式（自变量为Pokemon精灵的Defence和SP Defence），从而估测出这只Pokemon精灵$x$是Water（水）系的概率。

可能这里你会问，Gaussian Distribution（高斯分布）是什么呢？

Gaussian Distribution（高斯分布）

如果你不知道Gaussian Distribution（高斯分布），这里你可以简单把它理解成一个公式：
f μ , Σ ( x ) = 1 ( 2 π ) D 2 1 ∣ ∑ ∣ 1 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu,\Sigma}(x) = \frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\sum|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\} fμ,Σ​(x)=(2π)2D​1​∣∑∣21​1​exp{−21​(x−μ)TΣ−1(x−μ)}

其中:

• Input：向量x
• Output：取样为x的概率密度
• Gaussian Distribution（高斯分布）的形状决定因素：mean（期望）$\mu$和covariance matrix（协方差矩阵）$\Sigma$
• $\mu$不同，$\Sigma$相同，代表几率分布最高点的地方是不一样的

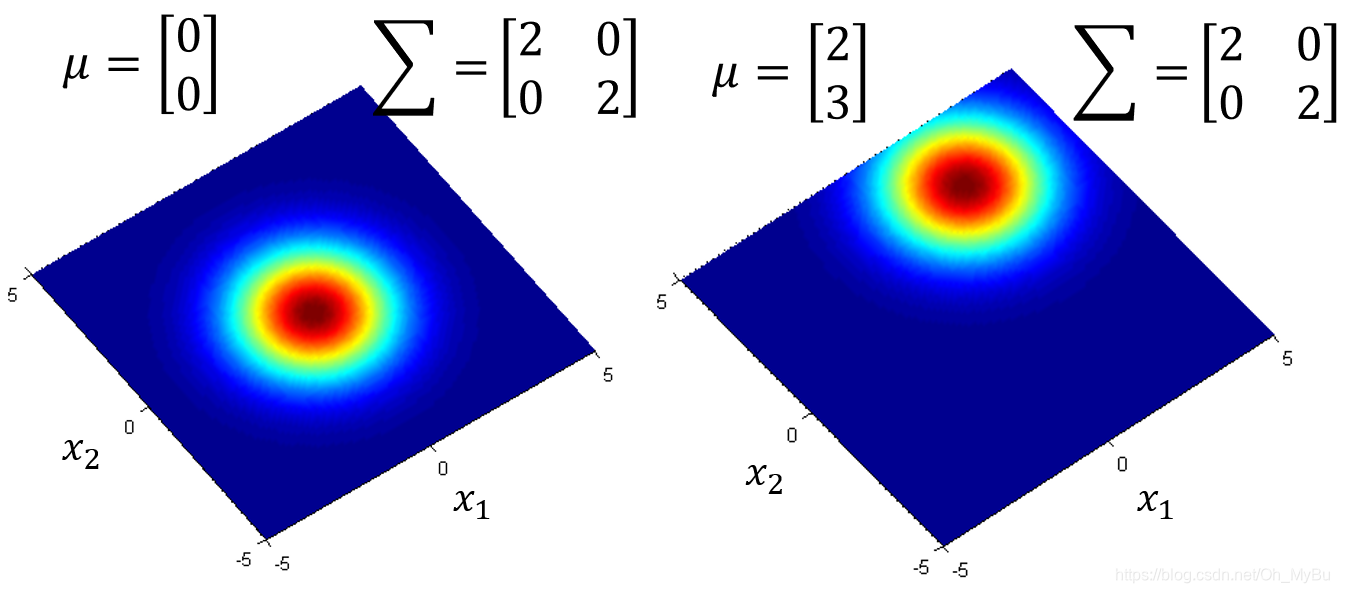
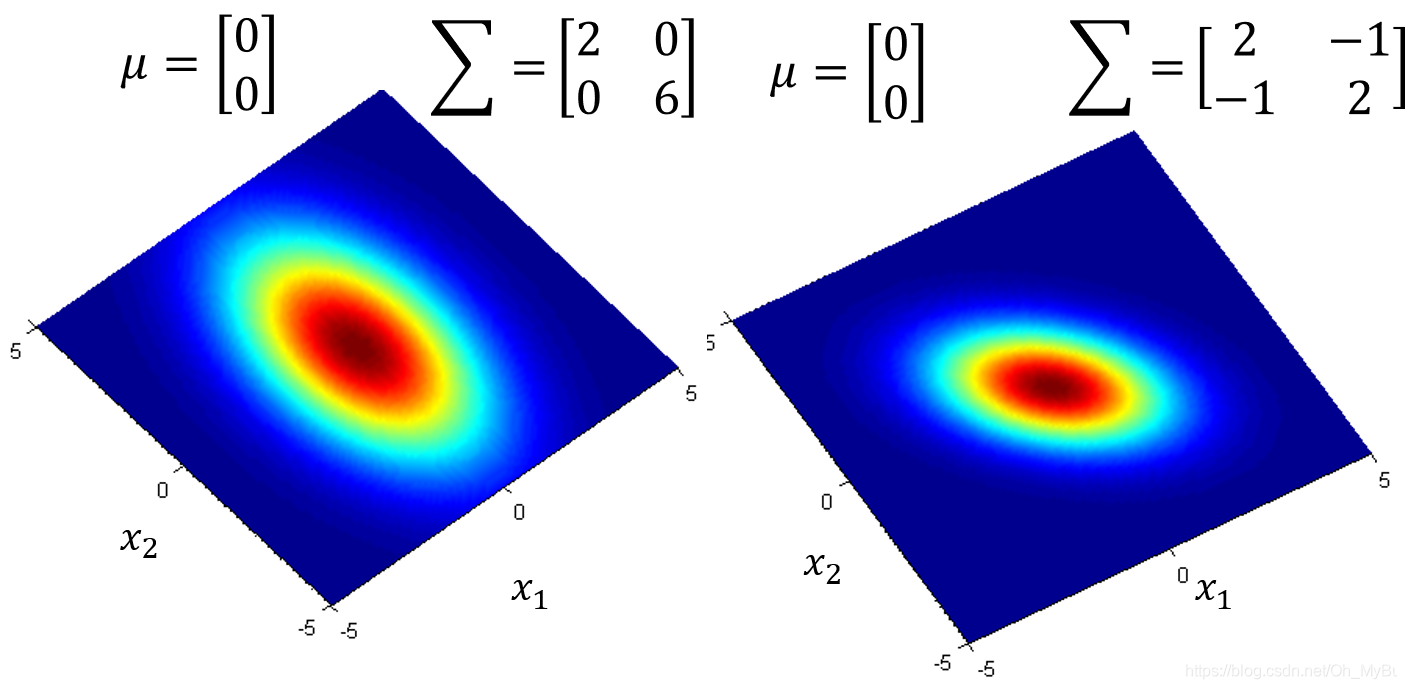
• $\mu$相同，$\Sigma$不同，代表几率分布最高点是一样的，但是分散程度是不一样的

Gaussian Distribution（高斯分布）举例说明

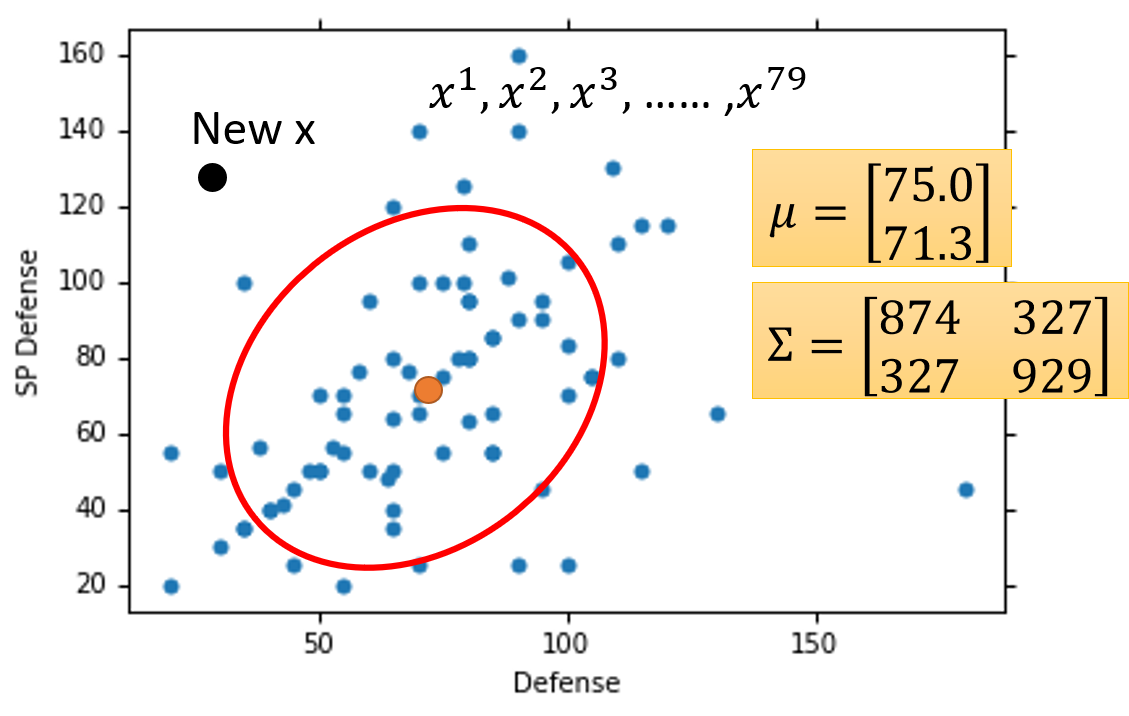
如上图，假设现在我们已知$\mu$（确定Gaussian Distribution最高点的位置）和$\Sigma$（确定Gaussian Distribution的形状），那我们就可以在Defence（防御力）和SP Defence（特殊防御力）分布图中确定Gaussian Distribution（高斯分布）的位置，现在如果有一个New $x$（新的Pokemon精灵$x$）出现，那么我们就可以将这个Pokemon精灵$x$代入一致的Gaussian Distribution（高斯分布）公式中，从而计算出这个新的Pokemon精灵$x$的是Water（水）系的概率。
f μ , Σ ( x ) = 1 ( 2 π ) D 2 1 ∣ ∑ ∣ 1 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } \\ f_{\mu,\Sigma}(x) = \frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\sum|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\} \\ fμ,Σ​(x)=(2π)2D​1​∣∑∣21​1​exp{−21​(x−μ)TΣ−1(x−μ)}

所以现在我们需要确定mean（期望）$\mu$和covariance matrix（协方差矩阵）$\Sigma$。

那怎么计算呢？

Maximum likelihood（极大似然估计）

我们现在已经知道，不同的$\mu$和$\Sigma$可以确定Gaussian Distribution（高斯分布），而不同的Gaussian Distribution（高斯分布）对于图中79个点得到的概率是不同的（different likelihood）。

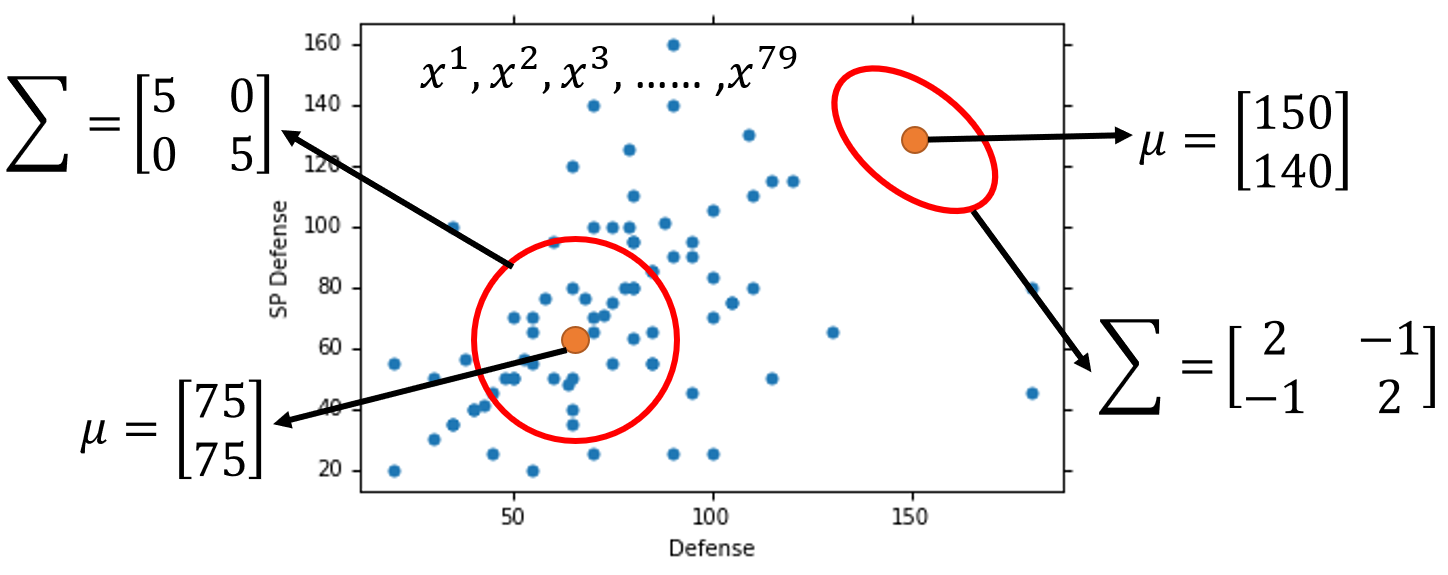
因为现在的这79个Pokemon精灵已经确定是Water（水）系的，所以我们最终得到的Gaussian Distribution（高斯分布）应该是能够让这79个点代入后概率是最大的。

即有Maximum likelihood（极大似然估计）式子：

$$L(\mu ,\Sigma )=f_{\mu ,\Sigma }(x^1)f_{\mu ,\Sigma }(x^2)f_{\mu ,\Sigma }(x^3)...f_{\mu ,\Sigma }(x^{7}9)$$
f μ , Σ ( x ) = 1 ( 2 π ) D 2 1 ∣ ∑ ∣ 1 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu,\Sigma}(x) = \frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\sum|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\}\\ fμ,Σ​(x)=(2π)2D​1​∣∑∣21​1​exp{−21​(x−μ)TΣ−1(x−μ)}
$${\mu }^{\ast },{\Sigma }^{\ast }=arg\underset{\mu ,\Sigma }{\max }L(\mu ,\Sigma )$$

这个式子由固定公式解（假装我们记住了这个公式解），即：
$${\mu }^{\ast }=\frac{1}{79}\sum _{n=1}^{79}{x}^n$$
$${\Sigma }^{\ast }=\frac{1}{79}\sum _{n=1}^{79}(x^n-{\mu }^{\ast })(x^n-{\mu }^{\ast }{)}^T$$

最终，我们将Water（水）系和Normal（一般）系的结果都计算出来后（如下图）

现在，我们就可以使用以下公式进行分类了。比如：如果$P(C_1|x)>0.5$，那么就可以说明$x$是属于Class 1（Water）

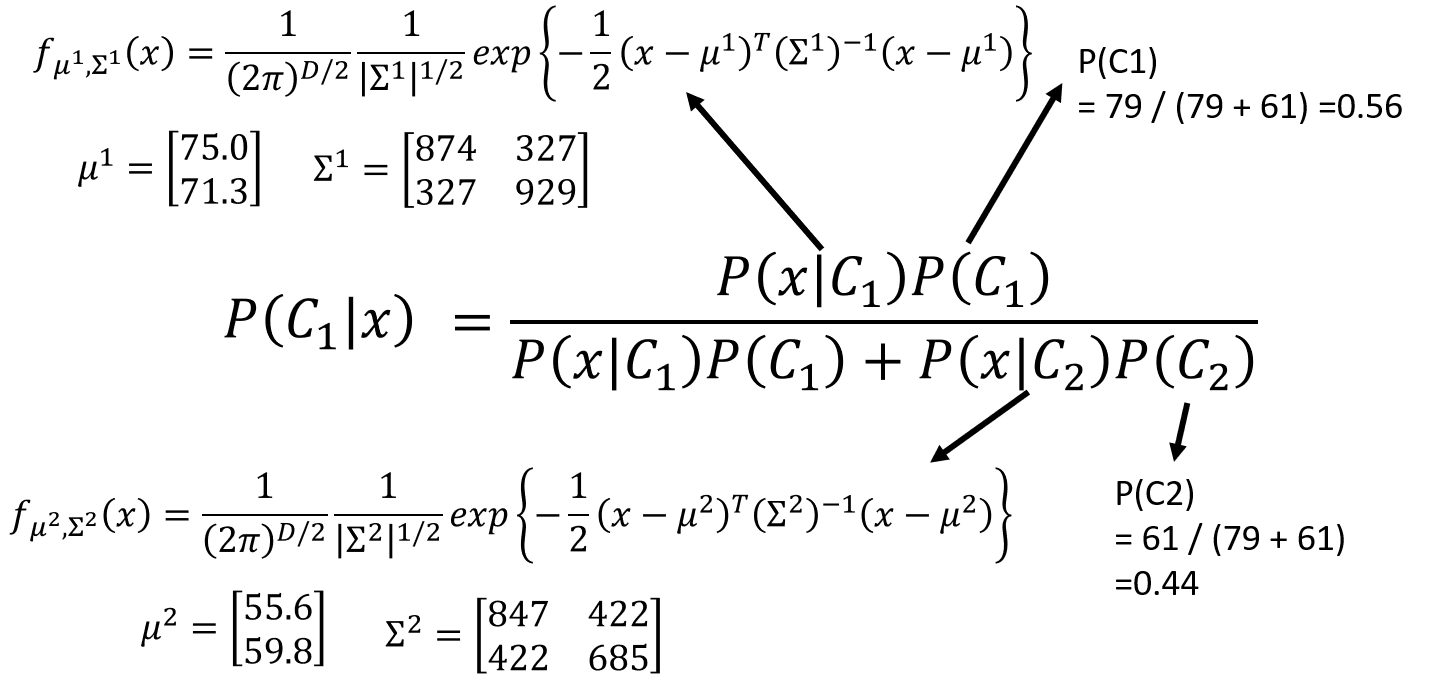
那最终结果怎么样呢？

How’s the results?

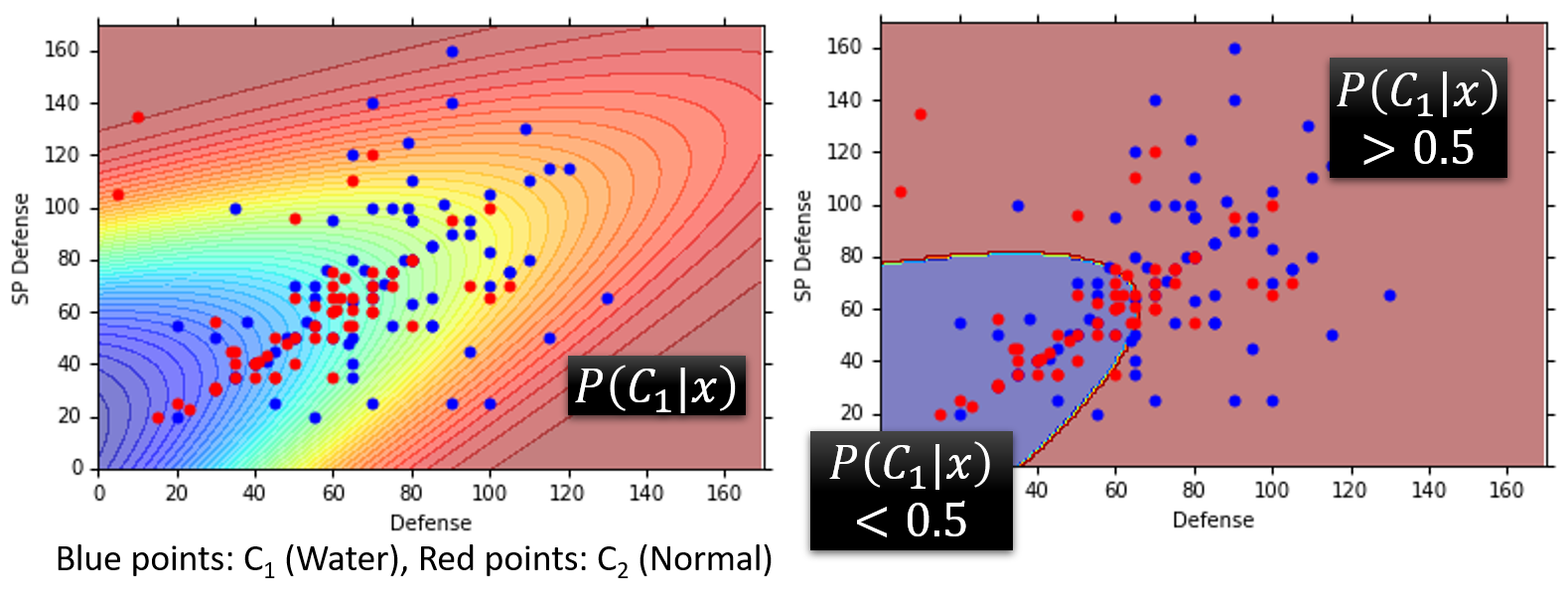
如上图，我们用两种图来表示最终的结果（图中的结果是对于Training Data而言的）

• 左图：图中红色点代表Class 2（Normal），蓝色点代表Class 1（Water），而图中不同的颜色代表不同的$P(C_1|x)$（红颜色代表概率大，蓝颜色代表概率小）
• 右图：图中以$P(C_1|x)=0.5$为分界线，蓝颜色代表$P(C_1|x)<0.5$，红颜色代表$P(C_1|x)>0.5$

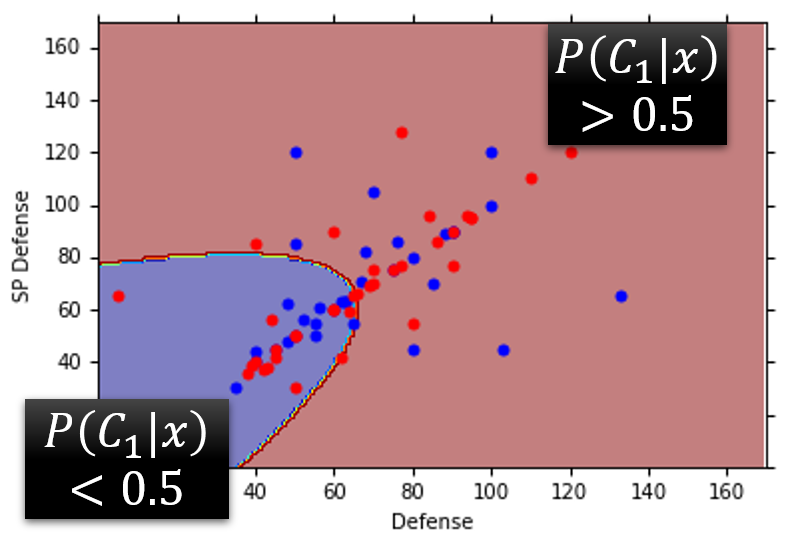
我们再来看一下Model在Testing Data中的结果，发现效果其实并不是这么好，准确率最终只有47%，不过没有关系，这也只是取了两个特征值Defence（防御力）和SP Defence（特殊防御力）的情况下的准确率。

如果我们将所有的特征值（Total、HP、Attack、SP Att、Defence、SP De、Speed）都放进Model进行Classification（分类）Testing Data结果会怎样呢？

• ${\mu }^1、{\mu }^2：7-dimvector$
• ${\Sigma }^1、{\Sigma }^2：7\times 7matrix$

最终准确率为54%…很糟糕，但是没关系！我们学习了Classification（分类）的过程！

文章就到这里，还请大家帮忙勘误！

（如果文章对您有帮助，您的点赞或评论就是对我写Blog最大的支持！谢谢~）