[Machine Learning] 回归（Regression）

回归(Regression)

---

KeyWords

• Linear Model（线性模型）
• Loss Function（损失函数）
• Gradient Descent（梯度下降）
• Generalization（泛化）
• Overfitting（过拟合）
• Regularization（正则化）

Regression可以做什么

如果说机器学习（Meachine Learning）要做的事情是要找一个Function，那么Regression要做的事情就是我们要找的那个Function是一个数值（Scalar）。如果我们要找的Function是一个数值，那么这种任务就叫做Regression。

那么Regression应用有哪些呢？

• 股票市场的预测

例如：找一个Function，Input是过去十年的股票市场的变动情况或资讯，Output是明天道琼工业指数的数值。

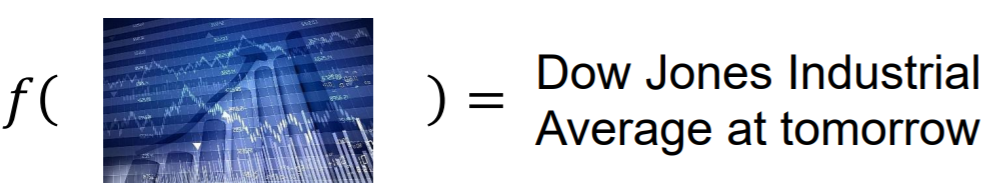
• 无人驾驶

例如：找一个Function，Input是无人车上的各个传感器（Sensor）所感应到的数据，Output是方向盘的角度。

• 推荐系统

例如：找一个Function，Input是某一个使用者A的特性和购买记录以及商品B的特性，Output是使用者A购买商品B的可能性

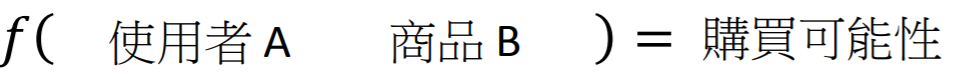
Regression应用举例

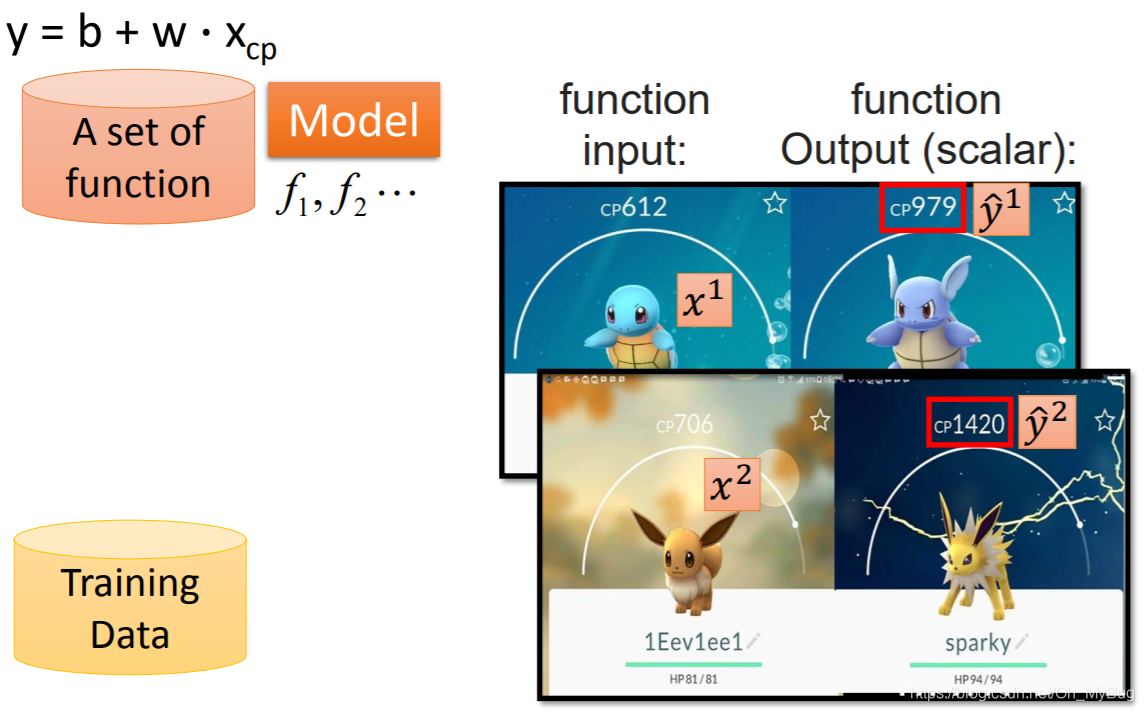
目标：预测进化后的Pokemon精灵的攻击力（CP值）

Input：Pokemon精灵的种种特性$x$（例如：当前Pokemon精灵进化前的CP值$x_{cp}$、物种$x_s$、HP值$x_{hp}$、重量$x_w$、高度$x_h$…）

Output：Pokemon精灵进化后的攻击力（CP值）

Step 1：Model—Linear Model（线性模型）

第一步是找一个模型（Model），所谓的模型，其实就是一个Function Set。这里的模型我们可以取作$y=b+\omega \cdot x_{cp}$（假设我们相信Pokemon精灵进化后的CP值与进化前的CP值有很大的关系）。

为什么说模型是一个Function Set呢？

这是因为当前我们的模型已经确认是$y=b+\omega \cdot x_{cp}$，而$\omega$和$b$就是模型的参数（Parameters），如果我们将一组特定的$\omega$和$b$值代入我们的模型$y=b+\omega \cdot x_{cp}$，那么就可以确定一个Function。因为我们的$\omega$和$b$可以取任何值，所以这些Function就构成了一个Function Set。因此，模型其实就是一个Function Set。而机器要做的，就是在这些无穷多的Function构成的Function Set中，挑选出一个最合适的Function。

这里所确定的模型$y=b+\omega \cdot x_{cp}$，我们称之为Linear Model（线性模型）

$$y=b+\sum {\omega }_i{x}_i$$
其中$x_i:x_{cp},x_{hp},x_w,x_h$，${\omega }_i:weight$（权重），$b:bias$（偏置）

这里可能会问，明明有这么多特征（$x_i$，$i=1,2,3,...$）可以用，为什么只选择$x_{cp}$呢？

这取决于你的Domain Knowledge(对一些领域的了解)，模型的特征并不是越多越好的，这会让计算变得复杂，所以我们在挑选特征的时候往往会选择认为和预测的目标关系比较大的特征。这里我们认为Pokemon精灵进化后的CP值与进化前的CP值有很大的关系，而对其他的信息缺少一定的认知或者认为关系很小。

Step 2：Goodness of Function

我们已经确定了一个Model，现在我们要做的是确定Funtion Set中的Function对预测结果是好是坏，并把好的Function挑选出来。

首先，我们需要收集一些Training Data（训练数据），Training Data内容包括：
$$((x^1,{\hat{y}}^1),(x^2,{\hat{y}}^2),...,(x^{n-1},{\hat{y}}^{n-1}),(x^n,{\hat{y}}^n))$$
其中，$x^i$代表第$i$只Pokemon精灵所包含的特征（目前只有进化前的CP值$x_{cp}$），${\hat{y}}^i$代表第$i$只Pokemon精灵进化后的实际CP值。

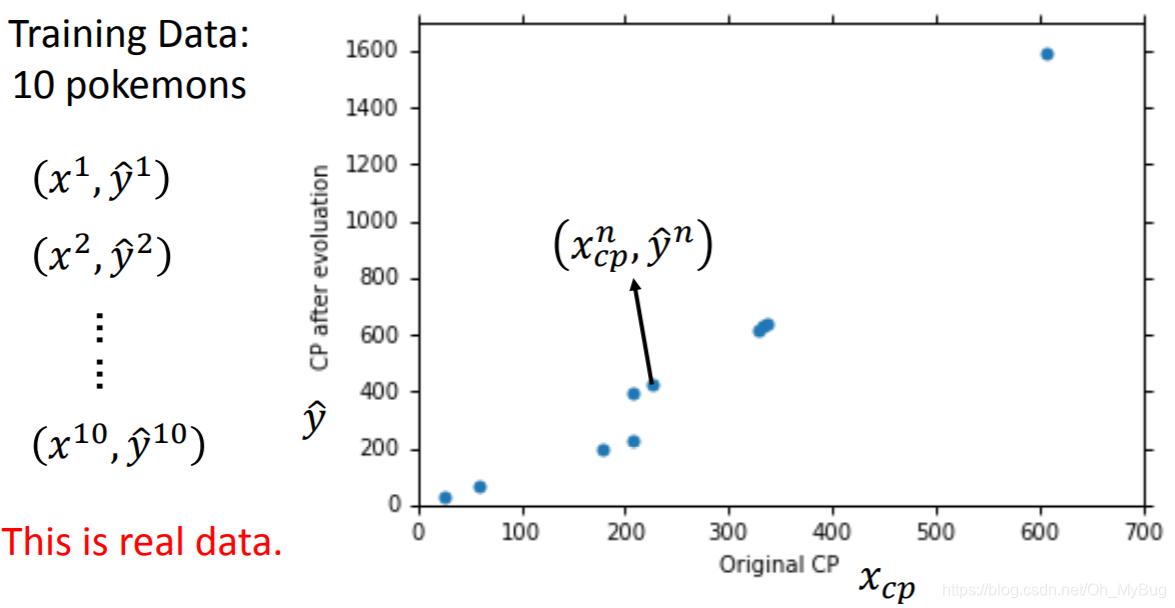
现在我们有十个关于Pokemon精灵的真实数据(n=10)，我们将它作为我们的训练数据，并作图（横坐标代表Pokemon精灵进化前的CP值，纵坐标代表Pokemon进化后的CP值）。

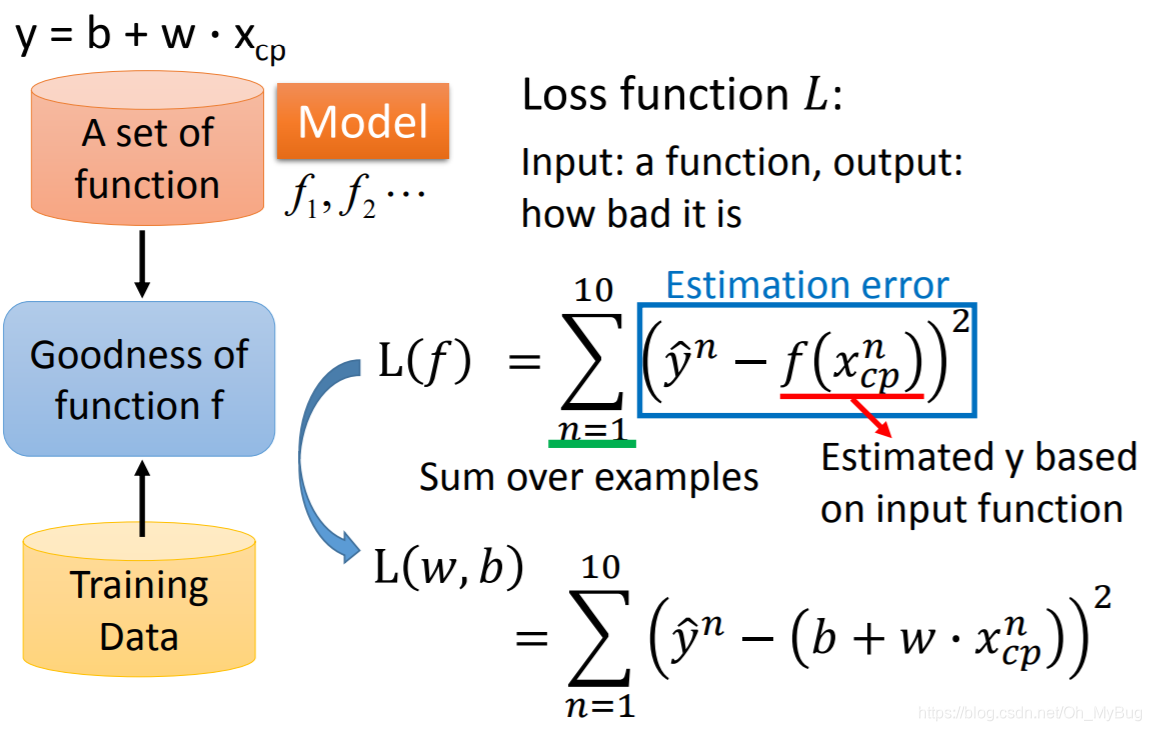
有了这些Data以后，我们就可以来衡量Function Set中的Function中的好坏。为了衡量这些Function中的好坏，我们需要引入一个新的Function—Loss Function。Loss Function的Input是Model（Function Set）里的一个Function，Output是这个Function的好坏。

这里Loss Function定义为：
$$L(f)=\sum _{n=1}^{10}({\hat{y}}^n-f(x_{cp}^n){)}^2$$
其中，$f(x_{cp}^n)$是Function Set中的Function基于输入Pokemon精灵进化前的CP值预测出来的Pokemon精灵进化后的CP值$y$。

因为$y=b+\omega \cdot x_{cp}$，所以Loss Function可以写作：
$$L(\omega ,b)=\sum _{n=1}^{10}({\hat{y}}^n-(b+\omega \cdot x_{cp}^n){)}^2$$

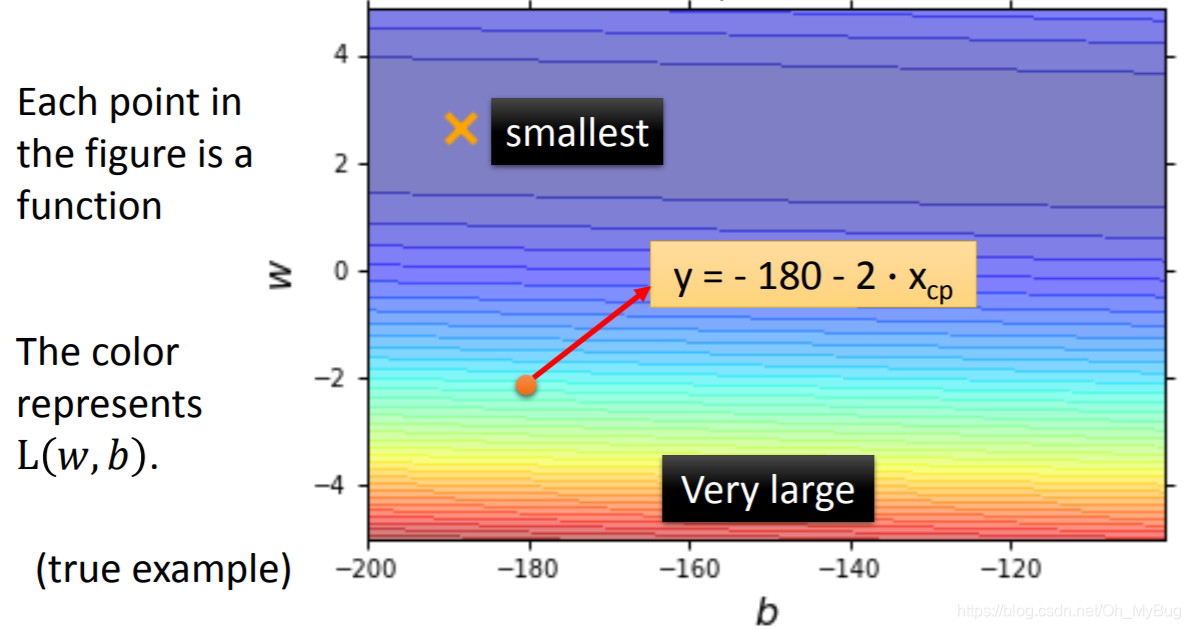
将Loss Function进行可视化（穷举在一定范围内的所有$\omega$和$b$），如上图，横坐标代表$b$值，纵坐标代表$\omega$，则图中的每个点代表一个Fuction，而颜色代表Loss Function在特定$\omega$和