Machine Learning —— Classification

Machine Learning —— Classification: Probabilistic Generative Model

Classification

基本概念

分类问题是找一个function，它的input是一个object，它的输出时这个object属于哪一个class。以宝可梦为例，已知宝可梦有18种属性，现在要解决的分类问题就是做一个宝可梦种类的分类器，我们要找到一个function，这个function的input是某只宝可梦，它的output是这只宝可梦属于哪一个类别。

输入数值化

对于宝可梦的分类问题，我们需要解决的第一个问题：怎么把某只宝可梦当做input
于是我们将宝可梦利用特性数值化：用一组数字来描述一只宝可梦的特性
以皮卡丘为例，我们可以用七种特性所组成的vector来描述它

How to classification

Training data for Classification

假设我们把编号400以下的宝可梦当做training data，编号400以上的当做testing data

Classification as Regression?

以binary classification为例，我们在training时让输入class1的输出为1，输入class2的输出为-1，那么在testing的时候，regression的output是一个数值，它接近1则说明它是class1，它接近-1说明是class2
如果这样做，会遇到什么问题
假设现在我们的model是$y=b+w_1{x}_1+w_2{x}_2$，input是两个feature，$x_1$和$x_2$
有两个class，蓝色的是class1，红色的是class2，假设我们真的找到这个function，如下图左边所示，绿色的线表示$0=b+w_1{x}_1+w_2{x}_2$，这种情况下，值接近-1的宝可梦都集中在绿线左上方，值接近1的宝可梦都集中在绿线的右下方
但是如果想下图右侧所示，如果要考虑右下角那些点的话，通过regression训练出来的model会是紫色这条分界线，因为相对于绿线，它“减小”了由右下角这些点所带来的error
Regression的output是连续性的数值，而classification要求的output是离散性质的点，很难找到一个Regression的function使大部分样本点的output都集中在某几个离散的点附近
因此Regression定义model的好坏的方式并不适用于classification

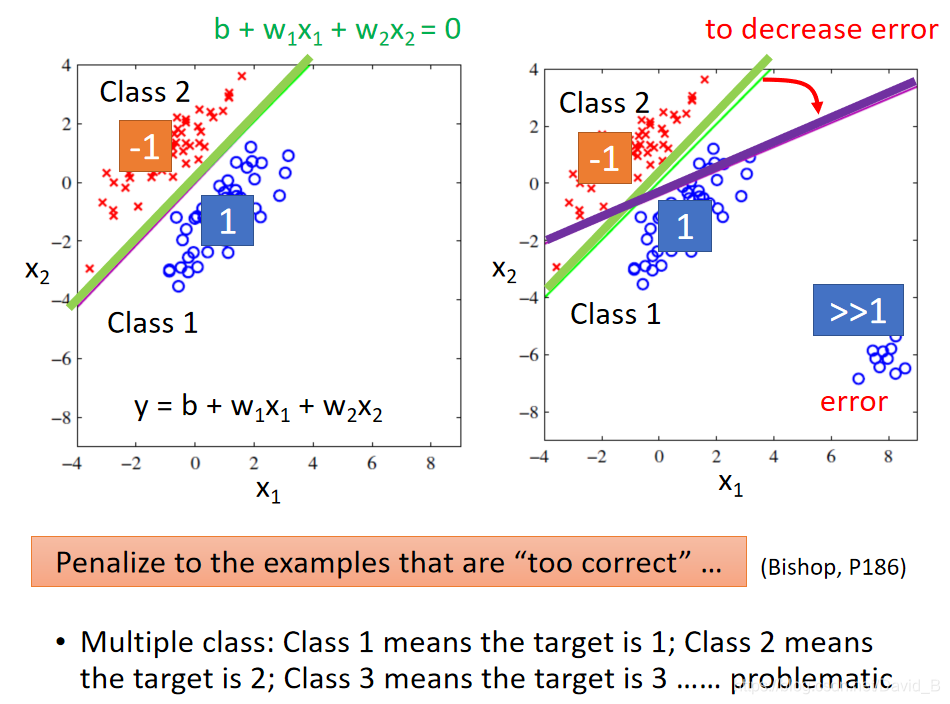
而且如果是多元分类的问题，把class1的target当做1，class2的target当做2，class3的target当做3，这样的做法是错误的，因为当这样做时，就会被Regression认为class1和class2的关系比较接近，class2和class3的关系比较接近，而class1和class3的关系比较疏远，但当这些class之间并没有什么特殊关系时，这样的标签用Regression是没有办法得到好的结果的

Ideal Alternative

Regression的output是一个real number，但在classification时，它的output是discrete
理想的方法是这样：
我们要找的function f(x) 里面会有另外一个function g(x)，当我们的input x输入后，如果g(x)>0，那么f(x)的输出就是class1，如果g(x)<0，那么就是class2

Loss function

我们可以把loss function定义成$L(f)={\sum }_n\delta (f(x^n)\ne {\hat{y}}^n)$，即这个model在所有的training data上predict预测错误的次数，也就是说分类错误的次数越少，这个function表现越好
这个loss function没有办法微分，于是用另一个solution来解决

Solution: Generative model

概率理论解释

假设我们考虑一个二元分类的问题，我们拿到一个input x，想知道这个x属于class1或class2的概率
这实际上是一个贝叶斯公式

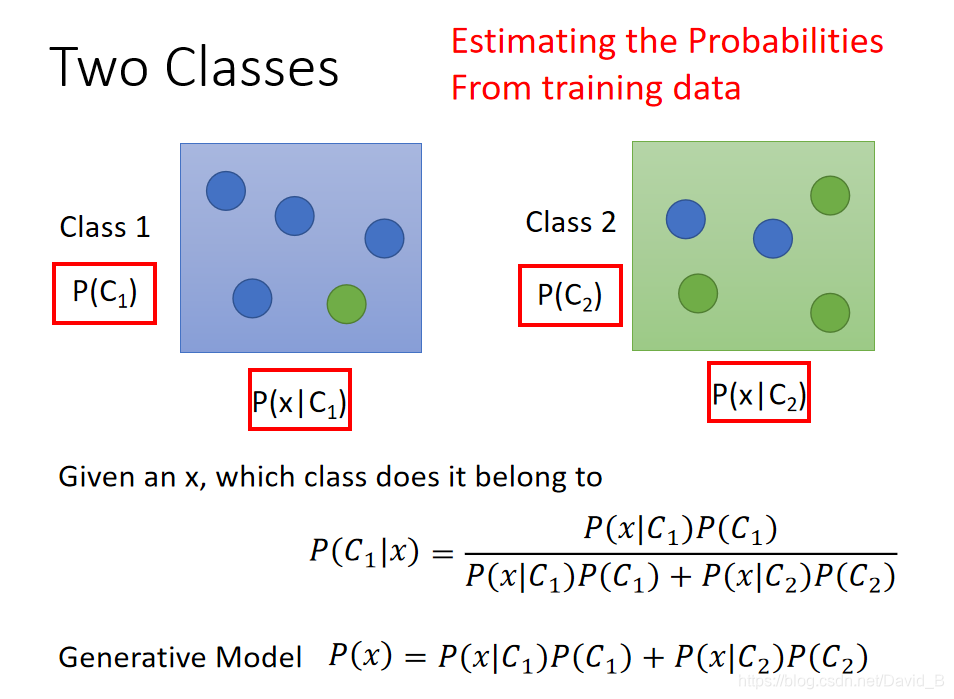
因此我们要知道x属于class1或class2的概率，只需要知道4个值：$P(C_1),P(x|C_1),P(C_2),P(x|C_2)$
我们可以从training data中估计出这四个值
这一整套想法叫做Generative model(生成模型)，有这个model的话，就可以拿它来生成x（如果可以计算每一个x出现的概率，就可以用这个distribution分布来生成x和sample x）

Prior

$P(C_1),P(C_2)$这两个概率被称为prior
在training data中，有79只水系宝可梦和61只一般系宝可梦，那么
$P(C_1)=79/(79+61)=0.56$
$P(C_1)=61/(79+61)=0.44$

问题是$P(x|C_1),,P(x|C_2)$怎么得到

Probability from Class

其实每一只宝可梦都可用一组特征值组成的向量来表示，在这个vector里一共有七种不同的feature，为了方便可视化，这里先只考虑Defense和SP Defense两种feature
假设图上的海龟的vector是[103 45]，虽然这个点在已有的数据中没有出现过，但是不可以认为它出现的概率为0，我们需要用已有的数据去估测海龟出现的可能性
假定水系宝可梦的Defense和SP Defense是从一个Gaussian的distribution里面sample出来的，上图只是采样了79个点之后得到的分布，但是从高斯分布里采样出海龟这个点的几率并不为0
那么如果从这79个已有的点，找到Gaussian distribution函数呢

Gaussian Distribution

高斯分布，里面的$\mu$表示均值，$\Sigma$表示方差，两者都是矩阵matrix，那么高斯函数的概率密度函数是：
$f_{\mu ,\Sigma }(x)=\frac{1}{(2\pi {)}^{\frac{D}{2}}}\frac{1}{|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$
从下图中可以看出，同样的$\Sigma$，不同的$\mu$，概率分布最高点的位置时不一样的

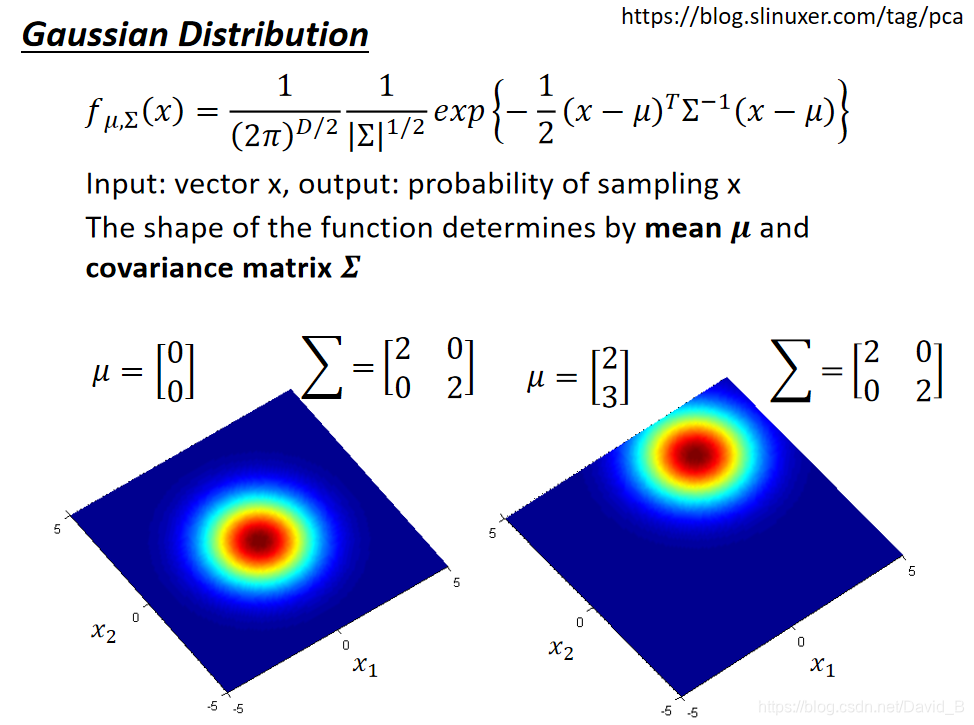
同样的$\mu$，不同的$\Sigma$，概率分布最高点的位置的位置一样，但是分布的密集程度不一样

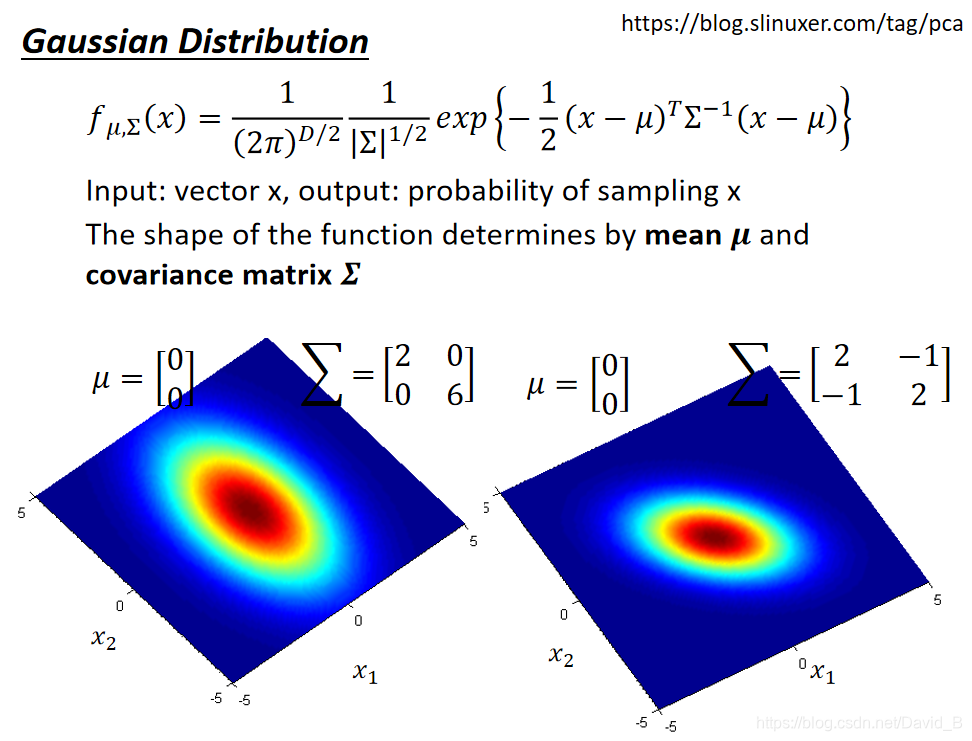
要找到这个Gaussian，只需要去估测出其均值$\mu$和协方差$\Sigma$即可
估计均值$\mu$和协方差$\Sigma$的方法就是极大似然估计法（Maximum Likelihood）：找出最特殊的那对$\mu$和$\Sigma$，从它们共同决定的高斯函数中再次采样出79个点，使“得到的分布情况与当前已知79个点的分布情况相同”这件事发生的可能性最大

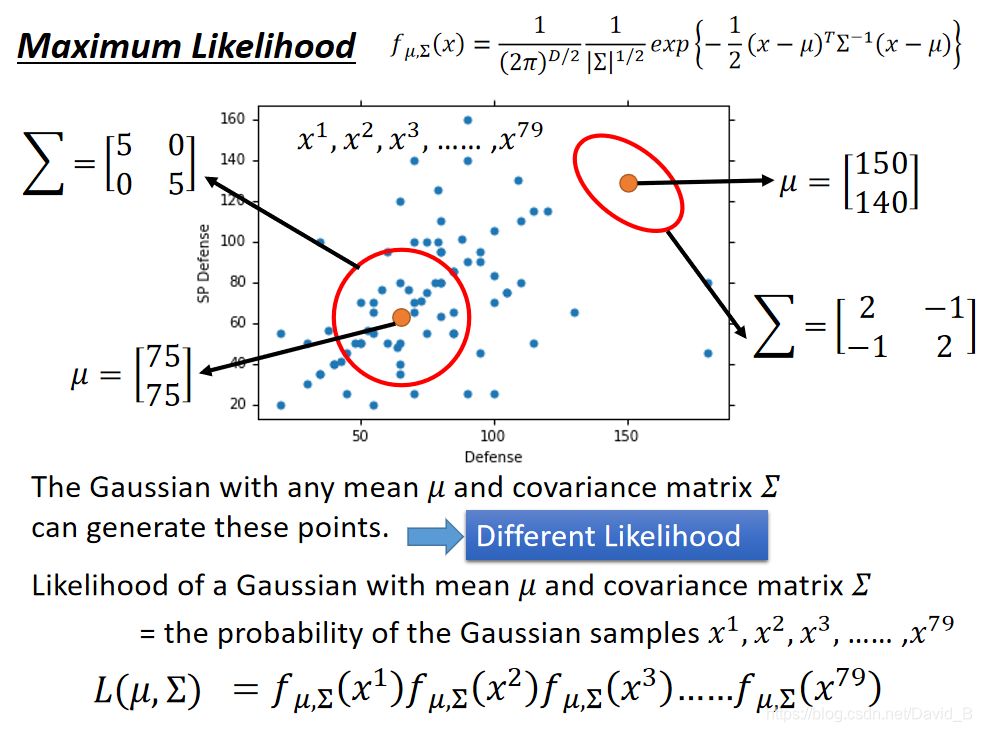
实际上$\mu$和$\Sigma$对应的高斯函数都有可能sample出和当前分布一致的样本点，就像上图中两个红色圆圈所代表的高斯函数，但肯定存在着发生概率最大的那一个Gaussian

ML：$L(\mu ,\Sigma )=f_{\mu ,\Sigma }(x^1)f_{\mu ,\Sigma }(x^2)...f_{\mu ,\Sigma }(x^{7}9)$，就是每个点都发生的概率之积，我们只需要将每一个点的data都代进去，分别对$\mu$和$\Sigma$求偏导，解出微分是0的点，即使L最大的那组参数，通过微分得到的高斯函数的$\mu$和$\Sigma$的最优解如下：

${\mu }^{\ast },{\Sigma }^{\ast }=arg\underset{\mu ,\Sigma }{\max }L(\mu ,\Sigma )$
$u^{\ast }=\frac{1}{79}{\sum }_{n=1}^{79}{x}^n{\Sigma }^{\ast }=\frac{1}{79}{\sum }_{n=1}^{79}(x^n-u^{\ast })(x^n-u^{\ast }{)}^T$

注：数学期望：$u=E(X)$，协方差：$\Sigma =cov(X,Y)=E[(X-Y)(X-Y{)}^T]$

根据上述的公式和数据，计算出class1的两个参数：

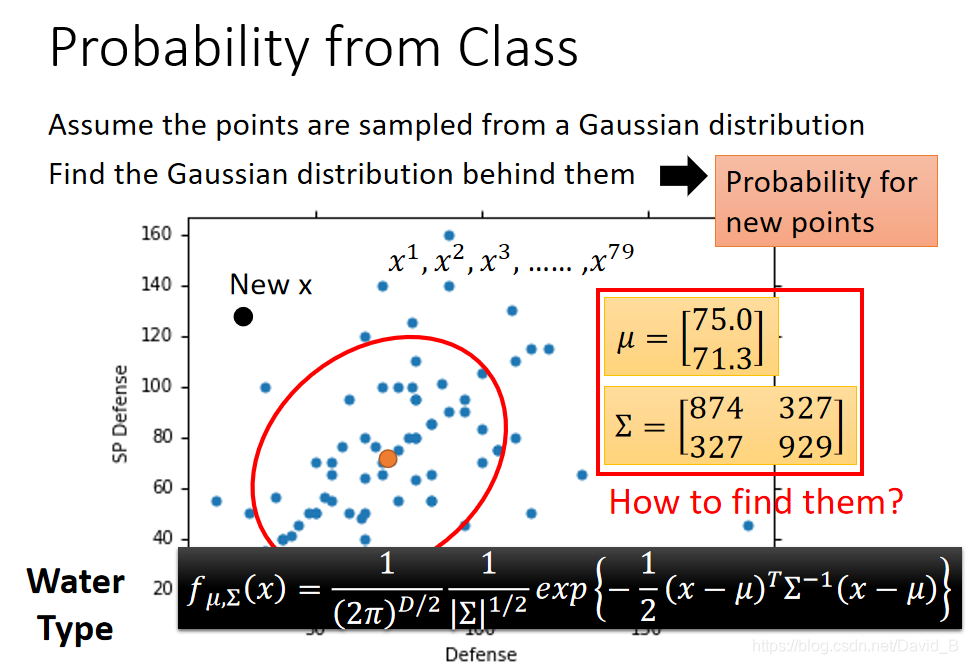
同理，用极大似然估计法计算出class2的两个参数，得到两个class的结果：

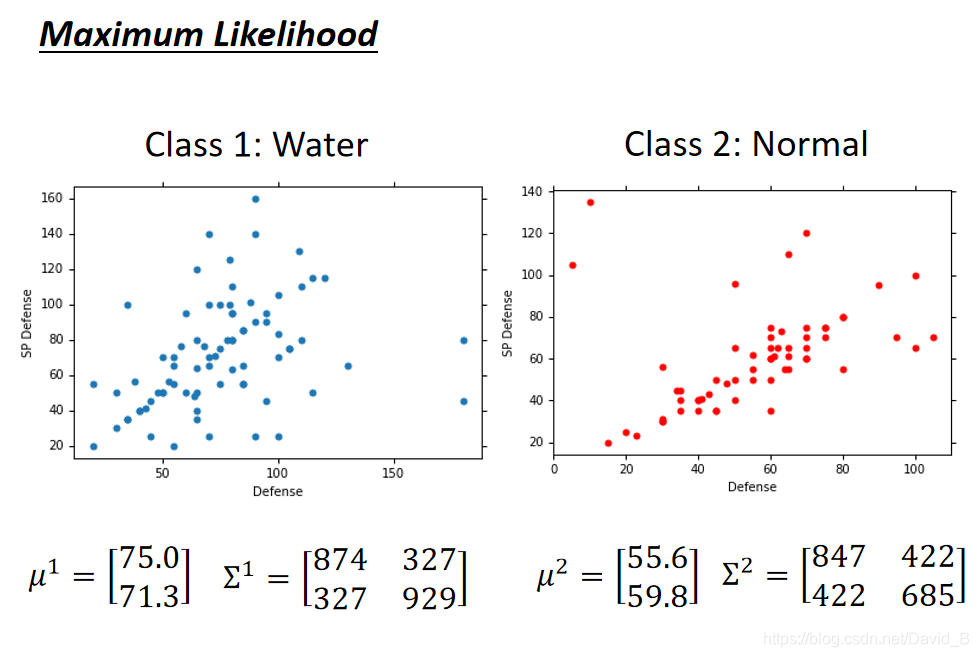
有了这些之后，我们可以得到$P(C_1),P(x|C_1),P(C_2),P(x|C_2)$，就可以开始做分类的问题了

Do Classification

现有的数据和具体分布

通过可视化得到的结果如下：

在左上角的图中，横轴是Defense，纵轴是SP Defense，蓝色的点是水系宝可梦的分布，红色的点是一般系宝可梦的分布，对图中的每一点都计算它是class1的概率$P(x|C_1)$，这个概率用颜色来表示，如果某点在红色区域，表示它是水系宝可梦的概率更大；如果该点在其他颜色的区域，表示它是水系宝可梦的概率比较小

因为我们做的是分类问题，因此令几率>0.5的点类别为1，几率<0.5的点类别为2，分出右上角图中的红色和蓝色两块区域

再把testing data上得到的结果可视化出来，即右下角的图，发现分的不是太好，正确率才是47%

我们之前用的只是Defense和SP Defense这两个参数，在二维空间上得到的效果不太好，也许在六维空间上看它们也许会分得更好，于是我们的$\mu$是一个6-dim的vector，$\Sigma$则是一个6*6的matrix，发现得到的准确率才64%，是否有办法改进的更好呢？

Modifying Model

之前使用的model并不常见，比较常见的做法是，不同的class可以share同一个covariance matrix
其实variance是跟input的feature size的平方成正比的，所以当feature的数量很大时，$\Sigma$的增加可以非常快，在这种情况下，给不同的Gaussian以不同的covariance matrix，会造成model的参数太多，而参数多会导致model的variance过大，出现overfitting的现象，因此Udine不同的class使用同一个covariance matrix，可以有效减小参数

把${\mu }_1$、${\mu }_2$和$\Sigma$合成一个极大似然函数，$\Sigma$是原先的${\Sigma }_1$和${\Sigma }_2$的加权
观察结果可以发现，class1和class2在没有用共同的$\Sigma$之前，分界线是一条曲线；在共用covariance matrix后，它们之间的分界线变成一条直线，这样的model，也可以称之为linear model（尽管Gaussian不是linear的，但是它分类的boundary是linear）

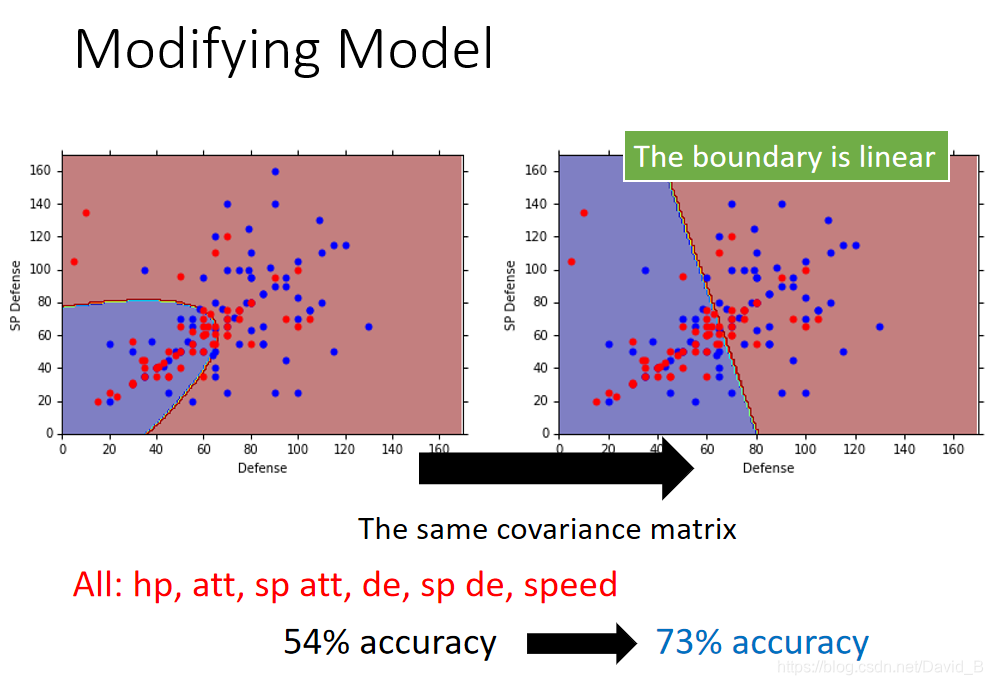
如果考虑所有的feature，并共用covariance的话，原来的54%的正确率会变成73%

Three Steps of Classification

回顾一下classification的三个步骤：

• Find a function set(model)
  这些required probability $P(C)$和probability distribution $P(x|C)$就是model的参数，选择不同的probability distribution就会得到不同的function，把这些不同参数的Gaussian distribution集合起来，就是一个model，如果不选择高数函数而选择其他分布函数，就会有新的model
• Goodness of function
  对于Gaussian distribution这个model来说，我们要评价的是决定这个高斯函数形状的均值$\mu$和协方差$\Sigma$两个参数的好坏，而极大似然函数$L(\mu ,\Sigma )$的输出值，可以用来评价参数好坏
• Find the best function
  找到最好的function，就是使$L(\mu ,\Sigma )$值最大的那组参数，实际上就是所有样本点的均值和协方差

$u^{\ast }=\frac{1}{n}{\sum }_{i=1}^n{x}^i{\Sigma }^{\ast }=\frac{1}{n}{\sum }_{n=1}^n(x^i-u^{\ast })(x^i-u^{\ast }{)}^T$

此处上标i表示第i个点，这里x是一个features的vector，用下标表示这个vector中的某个feature

Probability Distribution

Why Gaussian distribution

为什么使用Gaussian的model，而不选择其他的分布函数，当然也可以选择其他的分布函数，如果选择简单的分布函数（参数较少），那么bias就大，variance就小；如果选择复杂的分布函数，那么bias小，variance就大

Naive Bayes Classification（朴素贝叶斯分类法）

我们可以考虑这样一件事，假设$x=[x_1,x_2,x_3,...,x_k,...]$中的每一个dimension$x_k$的分布都是相互独立的，他们之间covariance都是0，那我们就可以把x产生的几率拆解成$x_1,x_2,x_3,...,x_k,...$产生的几率之积

这里每一个dimension的分布函数都是一维的Gaussian distribution，如果这样假设的话，原来多维度的Gaussian的covariance matrix变成是diagonal，在不是对角线的地方，都是0，这样就可以更加减少需要的参数量，就可以得到一个简单的model，这种方法称为朴素贝叶斯分类法

如果真的明确了所有feature之间是相互独立的，那么使用朴素贝叶斯分类法是很好的，但是如果feature之间不独立的话，那么bias就会很大

总之，寻找model的原则是尽量减少不必要的参数，但是必要的参数不能少

Analysis Posterior Probability

分析后验概率的表达式：
表达式上下同除以分子，得到$\sigma (z)=\frac{1}{1+e^{-z}}$，这个function叫做sigmoid function

这个S函数是已知逻辑函数，继续推导一下z真正的样子：



虽然推导过程比较复杂，但是得到的结果（当${\Sigma }_1$和${\Sigma }_2$加权组合成一个$\Sigma$），经过化简相消z就变成了一个linear的function，x的系数是一个vector w

$P(C_1|x)=\sigma (wx+b)$这个式子解释了当class1和class2共用$\Sigma$时，它们之间的boundary是linear的

在Generative model中，我们做的事情是，用某些方法找出$N_1,N_2,{\mu }_1,{\mu }_2,\Sigma$，找到这些参数之后就可以算出w和b，代入到$P(C_1|x)=\sigma (wx+b)$中，就可以计算概率

参考文章

https://github.com/Sakura-gh/ML-notes