[Machine Learning] 方向导数&梯度（Directional Derivative & Gradient）

Oh_MyBug

于 2020-02-13 17:09:03 发布

阅读量2.2k

点赞数 1

CC 4.0 BY-SA版权

分类专栏： Machine Learning 文章标签：机器学习线性代数

本文链接：https://blog.youkuaiyun.com/Oh_MyBug/article/details/104298853

本文详细探讨了方向导数和梯度的概念。方向导数描述了多元函数在特定方向上的变化率，而梯度则指向函数增长最快的方向。通过二元和三元函数的例子，解释了如何计算和理解这两个重要的数学工具，对于理解和优化机器学习中的损失函数具有重要意义。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

方向导数

首先，我们先来讨论一下函数 $y = f(x_1,x_2)$ 在一点P沿某一方向的变化率问题。

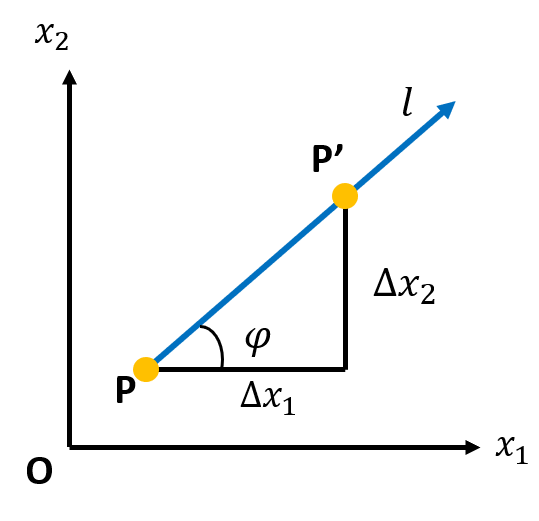
假设函数 $y = f(x_1,x_2)$ 在点 $P(x_1,x_2)$ 的某一邻域 $U (P)$ 内有定义，自点P引射线 $l$ 。设 $x$ 轴正向到射线 $l$ 的转角为 $φ\varphi$ ，并设 $P′(x1+Δx1,x2+Δx2)P'(x_1+\Delta x_1,x_2+\Delta x_2)$ 为 $l$ 上的另一点且 $P′∈U(P)P'\in U(P)$ (如图)。

那么我们可以定义：

函数的增量 $f(x1+Δx1,x2+Δx2)−f(x1,x2)f(x_1+\Delta x_1,x_2+\Delta x_2)-f(x_1,x_2)$ 与 $P P^{'}$ 两点间的距离 $ρ=(Δx1)2+(Δx2)2\rho = \sqrt{(\Delta x_1)^2+(\Delta x_2)^2}$ 的比值，当 $P^{'}$ 沿着 $l$ 趋于 $P$ 时，如果这个比值的极限存在，则称这个极限为函数在点 $P$ 沿方向 $l$ 的方向导数。记为：
$∂f∂l=lim⁡ρ→0f(x1+Δx1,x2+Δx2)−f(x1,x2)ρ\frac{\partial{f}}{\partial{l}} = \lim_{\rho\rightarrow 0} \frac{f(x_1+\Delta x_1,x_2+\Delta x_2)-f(x_1,x_2)}{\rho}$