论文阅读：Bone metastasis scintigram generation using generative adversarial learning with multi‐receptiv

Abstract

---

背景：

需要一种能扩大SPECT骨显像数据集的数据生成方法。

方法：

一种基于深度学习的SPECT骨显像生成模型。
采用生成对抗学习结构，提出骨转移显像生成模型（bone metastasis scintigram generation model，BMS-Gen）。
BMS-Gen采用多输入条件和多感受野学习来确保生成样本的真实性。
BMS-Gen采用生成对抗学习来保持生成样本的多样性。
BMS-Gen采用两阶段训练策略来提高生成样本的质量。

结果：

在 SPECT 骨转移显像图的临床数据上进行的实验评估显示了BMS-Gen的性能。
在FID（Fréchet初始距离）、MSE（均方误差）和PSNR（峰值信噪比）指标上获得了最好的总分。
在图像分类和分割任务中，BMS-Gen生成的样本的引入使F-1得分最大（最小）增加了3.01%（0.15%），DSC得分最大（最小）增加了6.83%（2.21%）。

1. Introduction

---

• ${}^{99m}\text{Tc-MDP}$ (technetium-99 methylene phosphonic acid)——锝-99亚甲基二膦酸盐
• $\text{SPECT}$ (single photon emission computed tomography)——单光子发射计算机断层扫描
• $\text{PET}$ (Positron Emission Tomography )——正电子发射断层扫描
• $\text{BM}$ (bone metastasis)——骨转移
• $\text{BMS-Gen}$ (bone metastasis scintigram generation model)——骨转移显像生成模型

使用 ${}^{99m}\text{Tc-MDP}$ 和 $\text{SPECT}$ 成像设备，可以在显像图中识别和显示 $\text{BM}$ 病变区域，该区域表现为放射性药物高摄取区域，通常称为“热点”。
SPECT骨显像的典型特征是空间分辨率低，骨转移病变在位置、大小和形状上不规则和不可预测。

两类CNN用于SPECT骨显像的自动分析：

1. 用于自动确定图像中是否存在骨转移，将其分类到相应的类别。
2. 用于通过分割图像来自动分离BM病灶。
   都需要大规模的SPECT骨显像样本。

生成对抗网络（GAN）是深度生成学习中最强大的框架之一，包含一个将潜在噪声空间映射为真实图像的生成器和一个用于区分数据库中样本与生成器生成样本的判别器。

主要挑战有两点：

1. SPECT骨显像较低的空间分辨率对从原始数据中生成细粒度的样本提出了很高的要求；
2. 骨转移病灶在位置、大小和形状方面的不可预测性和不规则性，使得基于深度学习的模型很难表征低分辨率的骨显像图像。

BMS-Gen特点：

1. 采用多输入条件和多感受野学习来确保生成样本的真实性。
2. 采用生成对抗学习来保持生成样本的多样性。
3. 采用两阶段训练策略来提高生成样本的质量。

贡献：

1. 确定了BM显像自动生成这一研究问题，基于深度学习的医学图像分析领域中的首个相关研究。
2. 提出了基于GAN的BMS-Gen模型。
3. 评估并验证了生成样本在提升下游任务性能中的实用性。

2. Methods

---

2.1 An overview——概述

---

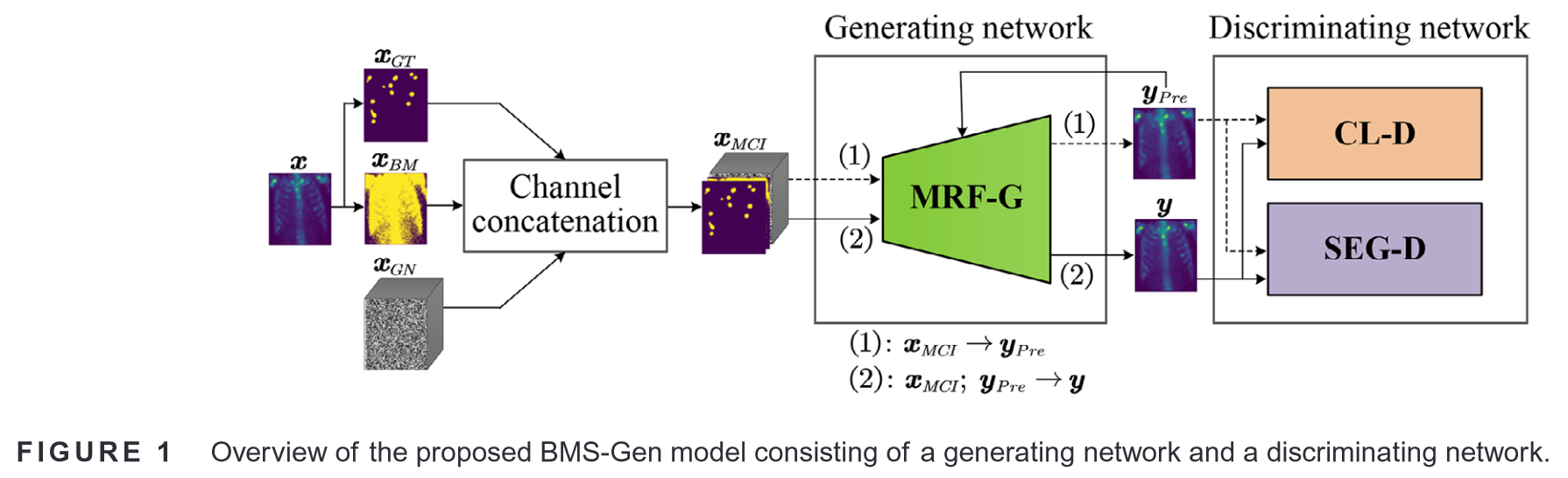
• $\text{MRF-G}$ (multi-receptive field generator)——多感受野生成器

组成：
生成网络和判别网络，生成网络使用定制的生成器——MRF-G。

样本：
病灶标签 $x_{GT}$ ，由经验丰富的专家使用开源工具LabelMe获取；
二值矩阵 $x_{BM}$ ，将x中的所有非零元素设为1、所有零元素设为0来创建二值矩阵；
3D高斯噪声 $x_{GN}$ ；
$x_{GT}$ 和 $x_{BM}$ 集成到 $x_{GN}$ 形成多通道输入 $x_{MCI}$ 。集成的 $x_{GT}$ 和 $x_{BM}$ 可视为3D噪声 $x_{GN}$ 的条件信息，代表多种条件。

初步训练阶段：
基于 $x_{MCI}$ 生成初步样本 $y_{Pre}$（即， $x_{MCI}\to y_{Pre}$）。

精炼训练阶段：
生成器MRF-G利用 $y_{Pre}$ 和 $x_{}$