\, \, \, \, \,之前提到过,在处理很多实际应用中的线性系统Ax=bAx=bAx=b求解问题的时候,由于采集大量样本导致矩阵AAA的行数大于列数,意味着方差的个数远远大于未知数个数,在这种情况下,由于数据偏差,方程之间就容易出现矛盾,因此真实情况建立的线性系统Ax=bAx=bAx=b大概率是无解的。
\, \, \, \, \,但是当我们并不需要一个十分精确的解,而只需一个接近解也足够用于研究的情况下。在线性系统Ax=bAx=bAx=b中,单单对于AxAxAx来说,其实AxAxAx表示的就是矩阵AAA的列空间,从向量乘法看AxAxAx表示成xxx中的未知数与矩阵AAA的列向量相乘再相加的形式x1⋅v⃗1+x2⋅v⃗2+x3⋅v⃗3⋯x_1 \cdot \vec v_1+x_2 \cdot \vec v_2+x_3 \cdot \vec v_3 \cdotsx1⋅v1+x2⋅v2+x3⋅v3⋯,而这个表示形式的就是矩阵AAA的列向量的生成空间。既然AxAxAx是矩阵AAA的列空间,继而线性系统Ax=bAx=bAx=b的求解问题可以理解成在AxAxAx这个列空间中找到向量bbb,如果向量bbb在矩阵AAA的列空间中的话,那么就肯定会有一个或多个xxx与它相对应。所以在获取一个实际线性问题的近似解的时候,通常是在矩阵AAA的列空间中找到一个离bbb最近的b′b'b′,转而求解线性系统Ax=b′Ax=b'Ax=b′的解来近似Ax=bAx=bAx=b。
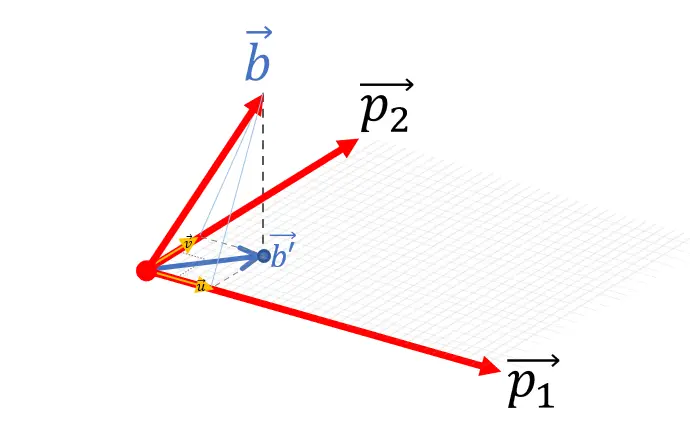
在矩阵AAA的列空间中寻找一个离b⃗\vec bb最近的向量b⃗′\vec b'b′,这个b⃗′\vec b'b′其实就是b⃗\vec bb在AAA的列空间的投影;
根据高中的几何知识可知b⃗\vec bb在AAA的列空间的投影b⃗′\vec b'b′是AAA的列空间中与向量b⃗\vec bb夹角最小的向量,也即方向上最接近的向量。
求出矩阵AAA的列空间的一组正交基(Gram-Schmidt过程),然后求出b⃗\vec bb分别到这组正交基各个分量的投影(一维投影问题),然后把这些投影分量加和在一起就是b⃗\vec bb在AAA的列空间的投影b⃗′\vec b'b′























 131
131

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










