线性代数：坐标系，坐标转换和线性变换

原创已于 2024-11-23 16:50:39 修改 · 2.7k 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数

于 2024-11-23 15:42:49 首次发布

线性代数专栏收录该内容

38 篇文章

订阅专栏

1、坐标系与坐标

(1)坐标系与空间的基

空间的基和坐标系两者之间属于一种一一对应的关系，坐标系也即空间的基，坐标系是理解空间的基的一种视角。 向量(点)在空间内的绝对位置不受坐标系的影响，坐标系只是改变描述点的相对位置信息。

我们通常描述一个点的坐标的时候都是基于一个参考标准进行描述的。当我们在说一个点的坐标的时候，如点 $A (12, 8)$ ，就已经是基于标准坐标系给出的二维欧式空间中 $A$ 点描述了。

二维平面的标准坐标系为 $e⃗2=(1,0)T\vec e_1 =(1,0)^{T} ,\ \vec e_2 =(1,0)^{T}$
三维平面的标准坐标系为 $e⃗3=(0,0,1)T\vec e_1 =(1,0,0)^{T} ,\ \vec e_2 =(0,1,0)^{T},\ \vec e_3 =(0,0,1)^{T}$
四维平面的标准坐标系为 $e⃗4=(0,0,0,1)T\vec e_1 =(1,0,0,0)^{T} ,\ \vec e_2 =(0,1,0,0)^{T},\ \vec e_3 =(0,0,1,0)^{T},\ \vec e_4 =(0,0,0,1)^{T}$
…

[ $例：点A(12,8)这个坐标是基于标准坐标系给出的A点在二维欧式空间的位置信息\color {darkred} {\small {例：点A(12,8)这个坐标是基于标准坐标系给出的A点在二维欧式空间的位置信息}}$ ]
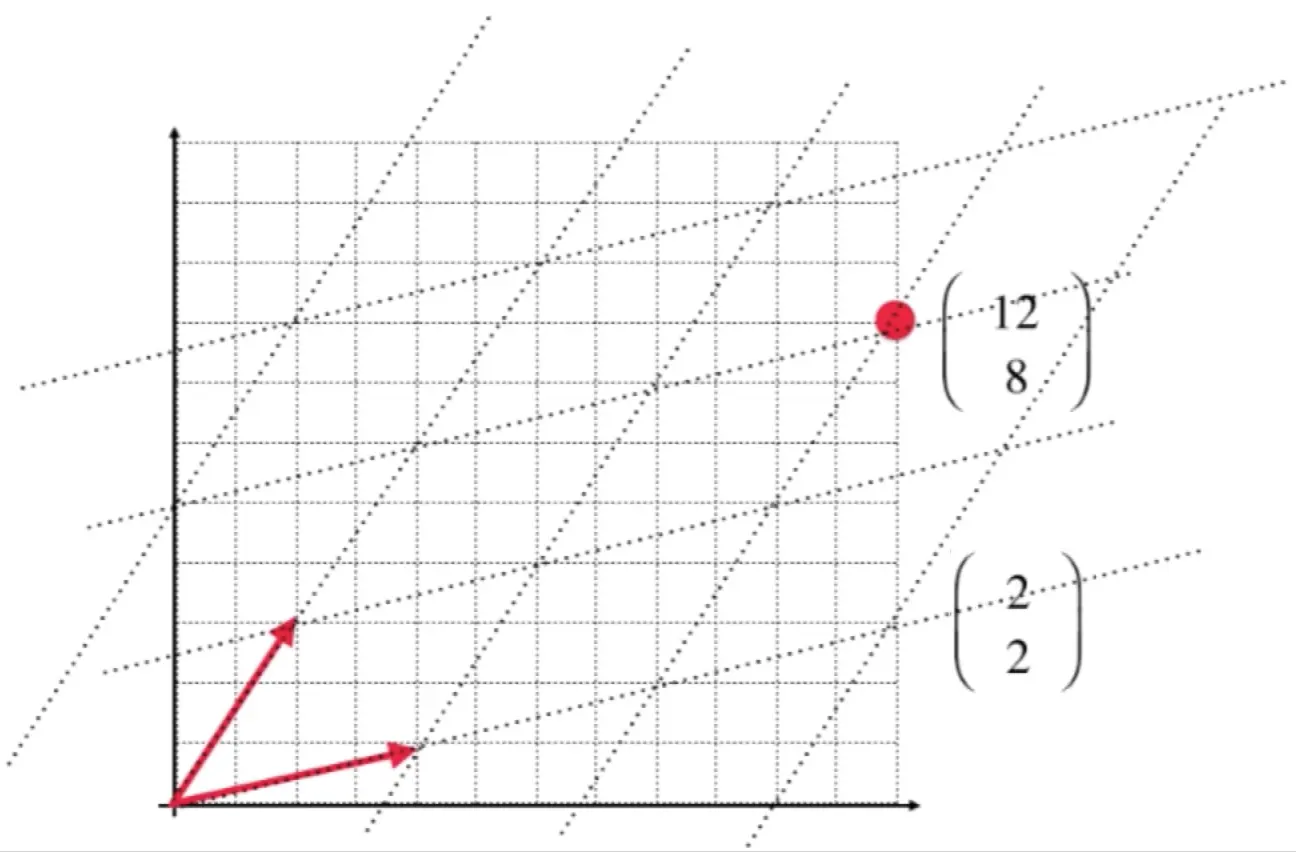
在一个二维平面直角坐标系，对于这个坐标系当我们定义了这个坐标系的两个坐标轴一个水平向右，一个竖直向上，并且定义好了什么是一个单位的概念，然后就能够描述在该坐标系下二维平面中 $A$ 点的坐标为 $A (12, 8)$ 。对于一个二维平面它有无数组基，那么当换一组基如 $u⃗(4,1),v⃗(2,3)\vec u(4,1) ,\vec v(2,3)$ 来表示整个二维平面，那么就建立一个新的坐标系,在这个坐标系下 $A$ 点的坐标又被描述为 $A (2, 2)$ ，这样来对于二维平面中的同一个点，就有了两种不同的描述方式。

在平面直角坐标系下描述点 $A (12, 8)$ $1208)\,\,\,\,\,\,\,\,\,\,\,\left (\begin{array} {c} \ 1&0 \\ 0&1 \end{array} \right ) \to \left (\begin{array}{c} \ 12 \\ 08 \end{array} \right )$
在 $u⃗(4,1),v⃗(2,3)\vec u(4,1) ,\vec v(2,3)$ 所表示的坐标系下描述点 $A (12, 8)$ $0202)\left (\begin{array}{c} \ 4&2 \\ 1&3 \end{array} \right ) \to \left (\begin{array}{c} \ 02\\ 02 \end{array} \right )$

在 $n$ 维空间中，当给定一组基， $任何一个向量都可以表示成这组基的线性组合\color {red} {{任何一个向量都可以表示成这组基的线性组合}}$ ，且表示方法唯一。

那么对于标准坐标系下的点 $A (12, 8)$ ，在向量组 $u⃗=(4,1)T,v⃗=(2,3)T\vec u=(4,1)^{T} ,\vec v=(2,3)^{T}$ 所表示的坐标系下，
就有: $(12,8)T=2⋅(4,1)T+2⋅(2,3)T=2⋅u⃗+2⋅v⃗(12,8)^{T} = 2\cdot (4,1)^{T} + 2 \cdot (2,3)^{T} = 2\cdot \vec u + 2\cdot \vec v$
$∴\therefore$ 在 $u⃗=(4,1)T,v⃗=(2,3)T\vec u=(4,1)^{T} ,\vec v=(2,3)^{T}$ 这组基下， $A$ 点可以表示为 $2$ 倍的 $u⃗\vec u$ 和 $v⃗\vec v$ 的线性组合，因此表示为 $A (2, 2)$

(2)坐标

如果给定向量空间 $V$ 的一组基 $,b⃗n}B=\{\vec b_1, \vec b_2,\vec b_3 , \cdots, \vec b_n \}$ ，以及 $V$ 中的一个向量 $x⃗\vec x$ ，则 $x⃗\vec x$ 一定可以被这组基线性表示。
假设: $x⃗=c1⋅b⃗1+c2⋅b⃗2+c3⋅b⃗3+⋯+cn⋅b⃗n\vec x = c_{1} \cdot \vec b_{1} + c_{2} \cdot \vec b_{2} + c_{3} \cdot \vec b_{3} + \cdots + c_{n} \cdot \vec b_{n}$
则称 $x⃗\vec x$ 在这组基 $B$ 下的坐标，为** $c_{1}, c_{2}, c_{3}, \cdots ,c_{n})^{T}$ **，记为： $[x⃗]B[\vec x]_{B}$ ，意思是当前给出的向量 $x⃗\vec x$ 的坐标是基于空间 $V$ 的 $B$ 这组基下给出的坐标。

一般情况下，当我们不写出参考基来标识一个向量，如向量 $x⃗=(12,8)\vec x= (12,8)$ ，就是因为我们描述向量都是默认参考 标准坐标系 $ε\varepsilon$ 给出的坐标,也即 $x⃗=[x⃗]ε=(12,8)\vec x = [\vec x]_{\varepsilon} = (12,8)$ ，而且即使空间的基是类似 $,v⃗\vec u ,\ , \vec v$ 这样的两个向量 $x⃗=(12,8)\vec x = (12,8)$ ，我们也还是用 标准坐标系 $ε\varepsilon$ 下的坐标来描述向量，不会用像 $[x⃗]B=(2,2)[\vec x]_{B} = (2,2)$ 这样的坐标来描述向量 $x⃗\vec x$ 。

标准基

$n$ 维标准基(Standard Basis) : 也即 $n$ 维标准坐标系 $,e⃗n}\varepsilon =\{\vec e_1 , \vec e_2 , \cdots ,\vec e_n \}$ ,最常用的坐标系。一个向量空间，只有一组标准基。

标准正交基(Orthonormal Basis): 一个向量空间，可以有无数组标准正交基。

正交基(Orthogonal Basis): 一个向量空间，可以有无数组正交基。

2、非标准坐标系坐标转换标准坐标系坐标

假设有一组基： $,b⃗n}B=\{\vec b_1, \vec b_2,\vec b_3 , \cdots, \vec b_n \}$ ，设立坐标转换矩阵 $∣)P_B== \left (\begin{array} {c} \ | \ \ \ \ |\ \ \ \ |\ \ \ \ \cdots \ \ \ | \\ \vec b_1,\vec b_2,\vec b_3,\cdots ,\vec b_n \\ \ | \ \ \ \ |\ \ \ \ |\ \ \ \ \cdots \ \ \ |\end{array} \right )$

对于在这组基下的一个向量 $[x⃗]B[\vec x]_{B}$ ，就有： $[x⃗]ε=PB⋅[x⃗]B[\vec x]_{\varepsilon} = P_{B} \cdot [\vec x]_{B}$ ，把 $B$ 坐标系下向量的坐标转换为标准坐标系下相应的坐标

结论证明:
对于一个二维平面的一组基 $u⃗(4,1),v⃗(2,3)\vec u(4,1) ,\vec v(2,3)$ ，在这组基所表示的坐标系下描述一个点 $x⃗=(2,2)\vec x = (2,2)$ 。
$∵\because$ 当不作特殊说明描述向量的时候都是在标准坐标系下进行描述的,所以基向量 $u⃗(4,1),v⃗(2,3)\vec u(4,1) ,\vec v(2,3)$ 都是在标准坐标系下进行表示的。
$∴\therefore$ $u⃗=(4,1)T=4e⃗1+1e⃗2\vec u = (4,1)^{T} =4 \vec e_{1} + 1\vec e_{2}$ $∴\therefore$ $v⃗=(2,3)T=2e⃗1+3e⃗2\vec v = (2,3)^{T} =2 \vec e_{1} + 3\vec e_{2}$

$∴[x⃗]B=[(2,2)T]B=2u⃗+2v⃗=2(4e⃗1+1e⃗2)+2(2e⃗1+3e⃗2)=12e⃗1+8e⃗2=[(12,8)T]ε\therefore [\vec x]_{B} = [(2,2)^{T}]_{B} = 2\vec u + 2\vec v = 2(4 \vec e_{1} + 1\vec e_{2}) + 2(2 \vec e_{1} + 3\vec e_{2}) = 12\vec e_{1} + 8\vec e_{2} = [(12,8)^{T}]_{\varepsilon}$

所以就有： $[x⃗]ε=PB⋅[x⃗]B[\vec x]_{\varepsilon} = P_{B} \cdot [\vec x]_{B}$

3、标准坐标系坐标准换非标准坐标系坐标

$PB−1⋅[x⃗]ε=PB−1⋅PB⋅[x⃗]B=[x⃗]BP_{B}^{-1} \cdot [\vec x]_{\varepsilon} = P_{B}^{-1} \cdot P_{B} \cdot [\vec x]_{B} = [\vec x]_{B}$ 该过程需要求矩阵 $P_{B}$ 的逆

4、任意两非标准坐标系之间的转换

假设有一组基 $,b⃗n}B=\{\vec b_1, \vec b_2,\vec b_3 , \cdots, \vec b_n \}$ 另一组基 $,c⃗n}C=\{\vec c_1, \vec c_2,\vec c_3 , \cdots, \vec c_n \}$
在 $B$ 这组基下表示的一个向量 $[x⃗]B[\vec x]_{B}$ ，求这个向量在 $C$ 这组基下的表示 $[x⃗]C[\vec x]_{C}$
借助标准坐标系与非标准坐标系的转换关系 $[x⃗]ε=PB⋅[x⃗]B[\vec x]_{\varepsilon} = P_{B} \cdot [\vec x]_{B}$
就有 $PB⋅[x⃗]B=[x⃗]ε=PC⋅[x⃗]CP_{B} \cdot [\vec x]_{B} = [\vec x]_{\varepsilon} = P_{C} \cdot [\vec x]_{C}$

$∴[x⃗]C=PC−1⋅PB⋅[x⃗]B\therefore [\vec x]_{C} = P^{-1}_{C} \cdot P_{B} \cdot [\vec x]_{B}$
其中 $PC−1⋅PBP^{-1}_{C} \cdot P_{B}$ 可以表示成 $PB→CP_{B \to C}$

对于空间 $V$ 两组基 $,b⃗n}B=\{\vec b_1, \vec b_2,\vec b_3 , \cdots, \vec b_n \}$ 和 $,e⃗n}C=\{\vec e_1, \vec e_2,\vec e_3 , \cdots, \vec e_n \}$ ,在这里，首先对于这两组基来说，里面的向量都是表示在标准坐标系下的，也即它们本应该写成 “ $[b⃗i]ε,[e⃗i]ε[\vec b_i]_{\varepsilon},[\vec e_i]_{\varepsilon}$ ” 这样的形式，只是我们省略了这组写法，默认它们就是标准坐标系下的向量表示。那么在这种情况下，由非标准坐标系转标准坐标系的推导 $[x⃗]ε=PB⋅[x⃗]B[\vec x]_{\varepsilon} = P_{B} \cdot [\vec x]_{B}$ ，其中转换矩阵 $PB→C=PBP_{B \to C} = P_{B}$ ，而这里的 $PB→CP_{B \to C}$ 矩阵就是在标准坐标系下表示的 $B$ 这组基的向量组成的矩阵 $[b⃗n]ε)P_{B \to C} = P_{B} = ( \begin{array}{c} \ [\vec b_1]_{\varepsilon} \ \ [\vec b_2]_{\varepsilon} \ \ [\vec b_3]_{\varepsilon} \ \ \cdots \ \ [\vec b_n]_{\varepsilon} \end{array} )$

据此，当我们知道了空间的一组基 $\{\vec b_1, \vec b_2,\vec b_3 , \cdots, \vec b_n \}$ 内的向量在另一组基 $\{\vec c_1, \vec c_2,\vec c_3 , \cdots, \vec c_n \}$ 所代表的坐标系下的表示的情况下，即 $⋯[b⃗n]C[\vec b_1]_{C},[\vec b_2]_{C} [\vec b_3]_{C} \ \ \cdots [\vec b_n]_{C}$ ，那么就有 $)P_{B \to C} = ( \ \ \ [\vec b_1]_{C}\ ,[\vec b_2]_{C} \ ,[\vec b_3]_{C} \ \ \cdots [\vec b_n]_{C} \ \ \ )$ ，B坐标系的向量转换C坐标系下的向量即 $[x⃗]B=PB→C⋅[x⃗]B[\vec x]_{B} = P_{B \to C} \cdot [\vec x]_{B}$ ，从而不借助标准坐标系完成转换非标准坐标系之间的转换。

示例说明

假设一组基 $\{ \vec b_{1} , \vec b_{2} \}\, \, \,$ 另一组基 $\{\vec c_{1} , \vec c_{2} \}$
其中知道 $b⃗2=3c⃗1+4c⃗2\vec b_{1} = 1\vec c_{1} + 2\vec c_{2} \ \ \ \ \ \vec b_{2} = 3\vec c_{1} + 4\vec c_{2}$
对于一个B坐标系的向量 $[x⃗]B=(2,2)T[\vec x]_B = (2,2)^T$ ，表示为C坐标系下，也即由C这组基线性表示即为
$)[\vec x]_B = (2,2)^T = 2\vec b_1 + 2 \vec b_2 = 2(\ 1\vec c_{1} + 2\vec c_{2} \ ) + 2(\ 3\vec c_{1} + 4\vec c_{2} \, )$
这对应的也就是以下矩阵乘法：
$1324)P_{B \to C} = ( \begin{array}{c} \ [\vec b_{1}]_{C} & [\vec b_{2}]_{C} \end{array} ) = \left( \begin{array}{c} \ 1&3 \\ 2&4 \end{array} \right )$

$22)=[x⃗]CP_{B \to C} \cdot [\vec x]_{B} = \left( \begin{array}{c} \ 1&3 \\ 2&4 \end{array} \right ) \cdot \left( \begin{array} {c} \ 2 \\ 2 \end{array} \right ) =[\vec x ]_{C}$

5、线性变换

在线性代数领域，主要研究的是线性变换，其中变换是一个函数，对向量的变换结果还是一个向量
当一个变换 $T (x)$ 称为线性变换时，必须满足:
$T(u⃗+v⃗)=T(u⃗)+T(v⃗)T(\vec u + \vec v) = T(\vec u ) + T(\vec v)$
$\vec u ) = c \cdot T(\vec u), c \in R$
意味着对向量进行线性变换后变换的结果仍然封闭在向量空间内，这样的变换就是线性变换。

在欧几里得空间，一个矩阵所表示的变换就是线性变换，一个矩阵所做的事情就是把一个向量 $x⃗\vec x$ 转换为另一个向量 $y⃗\vec y$ ,即 $\cdot \vec x = \vec y$

联系矩阵所代表的变换与坐标转换的关系:
对于一个变换矩阵 $(\vec u \ \ \vec v) = \left( \begin{array}{c} \ 4&2 \\ 1&3 \end{array} \right )$
这个矩阵 $A$ 本身又代表空间的一组基 $v⃗}A=\{ \vec u \ \ \vec v \}$ 所代表的坐标系变换到 标准坐标系 $ε\varepsilon$ 的坐标转换矩阵 $[v⃗]ε)=AP_{A \to \varepsilon} = ( [\vec u]_{\varepsilon} \ \ [\vec v]_{\varepsilon}) = A$
所以， $\cdot \vec x = [\vec x]_{\varepsilon}$ 就是把A坐标系下的 $x⃗\vec x$ 变换为标准坐标系下的坐标

示例 : $\left( \begin{array}{c} \ 1&0 \\ 0&-1 \end{array} \right )$ 表示一个翻转标准坐标系 $y$ 轴的变换
对于 $\cdot (2,3)^T = (2,-3)^T$ 这个等式来说，表示在 $A$ 坐标系下的点 $2,3)^T$ 转换为在标准坐标系 $ε\varepsilon$ 下表示为 $(2, - 3)$