P8647-整数二分查找

原题

• [ ] 引用link：https://www.acwing.com/activity/

整数二分的思想是什么？

核心点:找分界点

如果说对于一个数组，他的前一些满足性质1 后一些满足性质2 那么二分查找可以运用一定的方法寻找到最后一个满足性质1和最先满足性质2的点

eg：a[10]=1,3,9,101,791,2,8,100,10000,466 满足后5个都是双数 前五个都是单数
题目中要寻找最后一个单数或者最先一个复数 就可以用二分查找
思想类似于嵌套 优点是快 每一次都会删除掉原来的1/2
做法过程：1.先定义左右边界 l与r(左右边界的处理来源于题目的范围 如果没有可以用无穷大 如1e9）
2.定义中间值 写一个check函数判断中间点时这个性质和需要的答案的大小
当mid比答案大的时候 意味着答案在（l，mid） 那么右半部分不再需要了 r就更新成mid

模板均来自https://www.acwing.com/problem/content/791/
1.如果中坚持

当mid比答案小的时候 意味着mid在答案左边 意味着 答案在（mid，r)那么把l更新成mid
模板2

个人总结如何记忆：左减右加 仅有一个+1
如果是模板1 答案在（l,mid) 更新r 此时右加 else的l就要+1 且只有一个+1 mid不需要补+1
如果是模板2 答案在（mid,r）更新l 此时 左减 else的r要-1 此时函数里没有+1 给mid补上+1

看P8647题目：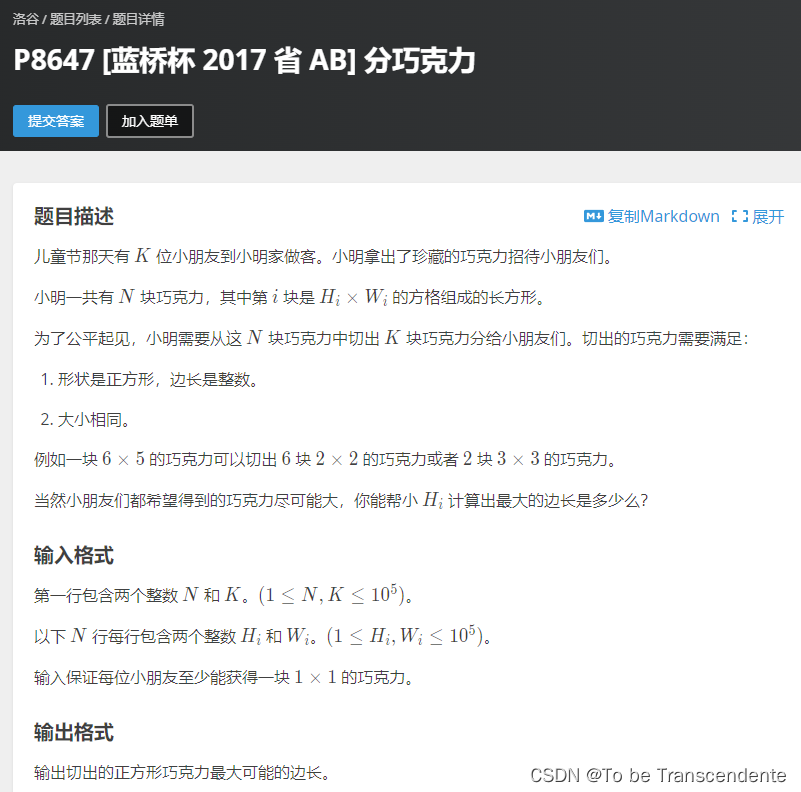
题目中问的是最大边长 可以理解成边长是一个数组（1-100000）—题目限制了方格大小（1，h)是可以被成功分的 (h+1,10^5)不能被分 这就是一个二分的题目
这里的l-r就可以当成边界 在二分完成后 l和r会重合 其中的任意一个就是答案。

#include<iostream>
using namespace std;
const int N=100010;
int h[N],w[N];
int n,k;
int check(int x)
{
	int ans=0;
	for(int i=0;i<n;i++) ans+=(h[i]/x)*(w[i]/x);//数学问题 一大块的蛋糕横分*竖分就是块数 正好c++给舍小数了
	return ans;
}
int main()
{
	cin>>n>>k;
	for(int i=0;i<n;i++)cin>>h[i]>>w[i];//输入
	int l=1,r=100010;
	while(l<r)
	{
		int mid=(l+r+1)/2;
		if(check(mid)>=k)l=mid;//check（mid)>k意思是 边长为mid时 可以分出比当前小朋友人数更多的蛋糕
		//那么如果我就想要k个小朋友的话 这每一块蛋糕的大小就小了，能分出更大的蛋糕 因为蛋糕面积*人数=总量
		//所以我需要的边长就在（mid,r)里，进入模板2
		else r=mid-1;
	}
	cout<<l<<endl;
	return 0;
 }