分析数据只能选择Excel？大错特错！

百分之九十九的人办公，要分析数据，目前他们最常用的仍然还是Excel。虽然Excel是当今最广泛使用的分析工具，简单易用，功能强大。但也存在一些问题，难以支撑企业数据分析的实际需求，以至于大家对Excel槽点满满，比如：

·满天都是飞来飞去的文件，Excel却没法提高共享效率

·人工周期性取数据好麻烦，Excel的事情还是得折腾IT小伙伴

·怎么控制数据权限，Excel想做好安全控制好难

·一旦查询大数据量，Excel就会卡到崩溃

那么如何解决Excel带来的限制呢？此时需要求助一款Excel融合分析工具——思迈特软件Smartbi 数据化运营平台。这是一款面向Excel用户，将Excel和BI有机结合，让业务人员能够轻松掌握的自助式数据分析工具。

接下来，就让小编给大家好好介绍一下思迈特软件Smartbi 数据化运营平台吧！

思迈特软件Smartbi 数据化运营平台的价值：

1.易学易用

使用思迈特软件Smartbi 数据化运营平台无需学习新的BI产品，会Excel就能完成BI分析，学习成本极低。

2.功能强大

思迈特软件Smartbi 数据化运营平台完整保留了Excel的数据加工以及数据分析能力，结合自助BI丰富的数据准备、数据共享、企业级安全管控。

3.资源复用

大量的Excel模板能够重复使用，企业资源可以得到充分利用。

4.效率提升

一线战斗单元可以随时在Excel获取最新的数据分析，告别重复导数。

思迈特软件Smartbi 数据化运营平台的主要功能：

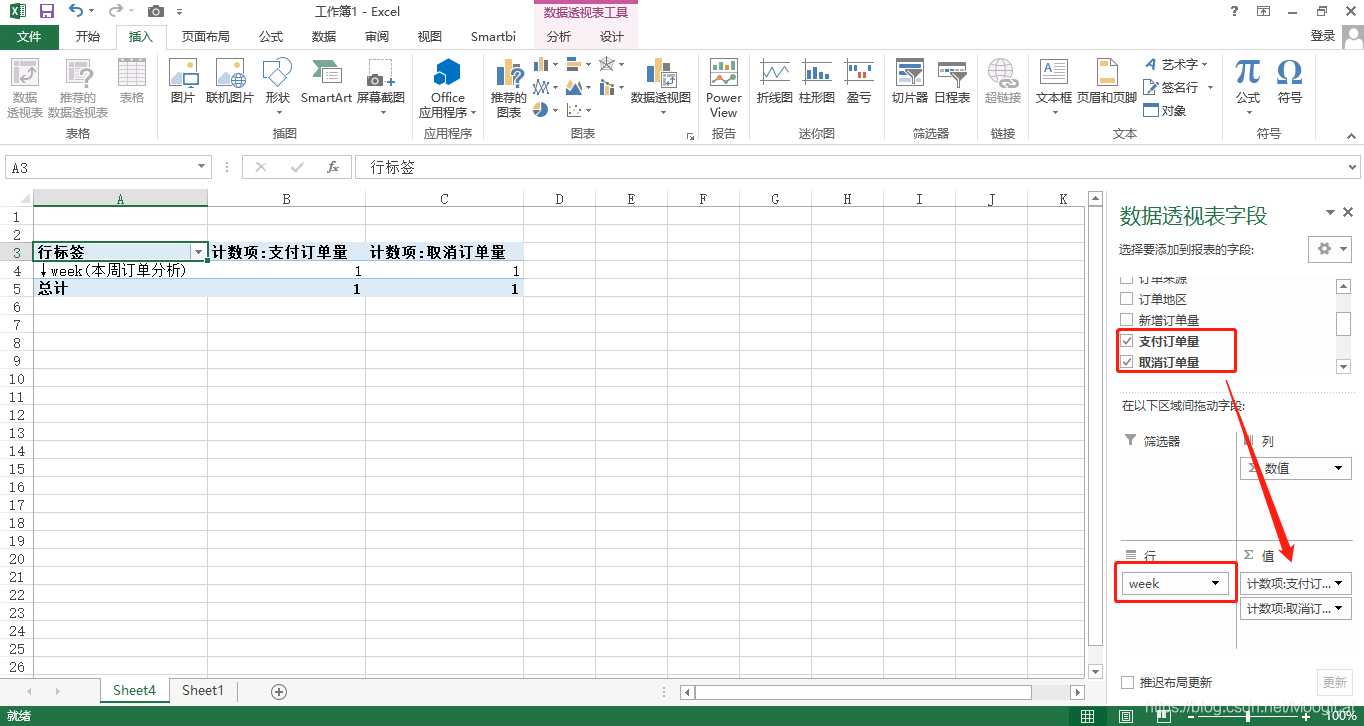
思迈特软件Smartbi 数据化运营平台可以使用Excel自行完成受控数据的提取，还可以将线下数据和线上数据无缝联合，实现数据的二次加工。思迈特软件Smartbi 数据化运营平台是通过Excel透视表来分析和展现数据的，模板和数据是分离的，因此模板可以重复使用，数据动态会自动更新，最后将数据动态安全发布共享到Web和手机端。

思迈特软件Smartbi 数据化运营平台的功能特色：

1.告别导数工作，数据准备自己搞定

2.线上线下数据混合

3.按照实际需求进行数据处理

4.复用模板进行分析

5.超大数据处理量

6.全面数据管控

7.分享成果，一联发布

思迈特软件统一登录平台