【VRPTW问题】基于碳黑四角蜂算法TGCOA求解带时间窗的骑手外卖配送路径规划问题（目标函数：最优路径成本含服务客户数量服务时间载量路径长度）附Matlab代码

原创于 2025-09-20 09:37:45 发布 · 951 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #开发语言

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎 往期回顾关注个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🔥 内容介绍

在即时外卖配送场景中，带时间窗的骑手路径规划（Vehicle Routing Problem with Time Windows, VRPTW）是提升配送效率、降低运营成本的核心环节。该问题需在 “骑手载量有限”“客户服务时间窗约束”“多目标成本优化”（服务客户数量、服务时间、载量利用率、路径长度）下，为多骑手规划最优配送路径，传统算法（如遗传算法、蚁群算法）存在 “收敛速度慢”“多目标平衡难”“复杂约束适配性差” 等问题。碳黑四角蜂算法（Tarantula Hawk-Cuckoo Optimization Algorithm, TGCOA）融合了沙漠蛛蜂的 “猎物搜索 - 精准攻击” 行为与布谷鸟的 “巢寄生” 策略，具备全局搜索能力强、多目标优化效率高、约束处理灵活的优势，为 VRPTW 问题提供了高效解决方案。本文将从 VRPTW 问题建模、TGCOA 算法原理、算法适配设计、实验验证四方面，解析该算法如何实现外卖配送路径的多目标优化。

二、碳黑四角蜂算法（TGCOA）的核心原理

TGCOA 算法源于两种昆虫的生物行为：沙漠蛛蜂（Tarantula Hawk）的 “远距离搜索 - 精准定位 - 高效攻击” 策略，与布谷鸟（Cuckoo）的 “巢寄生 - 优质巢保留” 机制，通过融合两种行为的优势，实现全局搜索与局部优化的平衡，适配 VRPTW 问题的多目标优化需求。

2.1 算法的生物行为抽象

TGCOA 将外卖配送路径规划类比为 “蜂群寻找最优食物源（客户）并规划采集路径”，核心生物行为抽象为算法操作：

沙漠蛛蜂的搜索与攻击行为：

远距离搜索：沙漠蛛蜂通过视觉与嗅觉远距离探测猎物（客户），对应算法中 “全局随机搜索”，生成多样化初始路径方案；

精准定位：发现猎物后，蛛蜂通过地形分析调整飞行轨迹（避开障碍），对应算法中 “局部路径优化”，根据客户时间窗、载量约束调整路径节点顺序；

高效攻击：蛛蜂对猎物实施精准攻击（最小化能量消耗），对应算法中 “目标函数导向优化”，优先提升服务客户数量与载量利用率。

布谷鸟的巢寄生与优质巢保留：

巢寄生：布谷鸟将卵产入其他鸟巢（利用优质巢资源），对应算法中 “路径信息共享”，将优质骑手的路径片段迁移到其他骑手路径中；

优质巢保留：布谷鸟优先选择孵化率高的优质巢，对应算法中 “非支配排序”，保留多目标优化中的优质路径方案，淘汰劣质方案。

⛳️ 运行结果

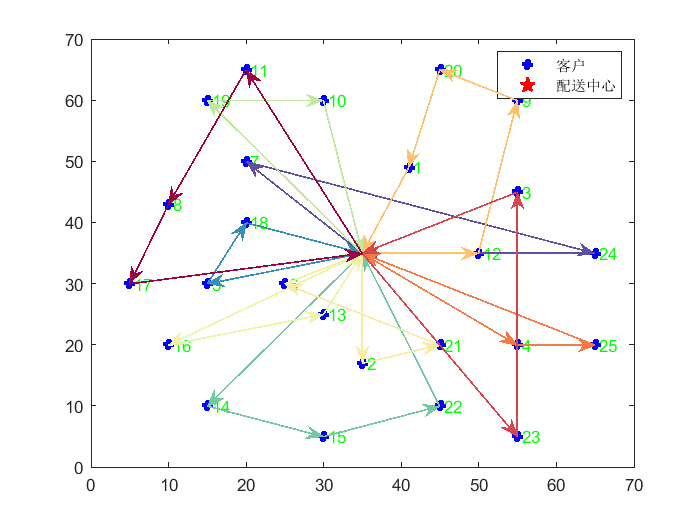
📣 部分代码

%% credits and where the function came from

% The colors are largely taken from:

% http://colorbrewer2.org and Cynthia Brewer, Mark Harrower and The Pennsylvania State University

% She studied this from a phsychometric perspective and crafted the colors

% beautifully.

% I made choices from the many there to decide the nicest once for plotting

% lines in Matlab. I also made a small change to one of the colors I

% thought was a bit too bright. In addition some interpolation is going on

% for the sequential line styles.

function lineStyles=linspecer(N,varargin)

if nargin==0 % return a colormap

lineStyles = linspecer(128);

return;

end

if ischar(N)

lineStyles = linspecer(128,N);

return;

end

if N<=0 % its empty, nothing else to do here

lineStyles=[];

return;

end

% interperet varagin

qualFlag = 0;

colorblindFlag = 0;

if ~isempty(varargin)>0 % you set a parameter?

switch lower(varargin{1})

case {'qualitative','qua'}

if N>12 % go home, you just can't get this.

warning('qualitiative is not possible for greater than 12 items, please reconsider');

else

if N>9

warning(['Default may be nicer for ' num2str(N) ' for clearer colors use: whitebg(''black''); ']);

end

qualFlag = 1;

case {'sequential','seq'}

lineStyles = colorm(N);

return;

case {'white','whitefade'}

lineStyles = whiteFade(N);return;

case 'red'

lineStyles = whiteFade(N,'red');return;

case 'blue'

lineStyles = whiteFade(N,'blue');return;

case 'green'

lineStyles = whiteFade(N,'green');return;

case {'gray','grey'}

lineStyles = whiteFade(N,'gray');return;

case {'colorblind'}

colorblindFlag = 1;

otherwise

warning(['parameter ''' varargin{1} ''' not recognized']);

end

% *.95

% predefine some colormaps

set3 = colorBrew2mat({[141, 211, 199];[ 255, 237, 111];[ 190, 186, 218];[ 251, 128, 114];[ 128, 177, 211];[ 253, 180, 98];[ 179, 222, 105];[ 188, 128, 189];[ 217, 217, 217];[ 204, 235, 197];[ 252, 205, 229];[ 255, 255, 179]}');

set1JL = brighten(colorBrew2mat({[228, 26, 28];[ 55, 126, 184]; [ 77, 175, 74];[ 255, 127, 0];[ 255, 237, 111]*.85;[ 166, 86, 40];[ 247, 129, 191];[ 153, 153, 153];[ 152, 78, 163]}'));

set1 = brighten(colorBrew2mat({[ 55, 126, 184]*.85;[228, 26, 28];[ 77, 175, 74];[ 255, 127, 0];[ 152, 78, 163]}),.8);

% colorblindSet = {[215,25,28];[253,174,97];[171,217,233];[44,123,182]};

colorblindSet = {[215,25,28];[253,174,97];[171,217,233]*.8;[44,123,182]*.8};

set3 = dim(set3,.93);

if colorblindFlag

switch N

% sorry about this line folks. kind of legacy here because I used to

% use individual 1x3 cells instead of nx3 arrays

case 4

lineStyles = colorBrew2mat(colorblindSet);

otherwise

colorblindFlag = false;

warning('sorry unsupported colorblind set for this number, using regular types');

end

if ~colorblindFlag

switch N

case 1

lineStyles = { [ 55, 126, 184]/255};

case {2, 3, 4, 5 }

lineStyles = set1(1:N);

case {6 , 7, 8, 9}

lineStyles = set1JL(1:N)';

case {10, 11, 12}

if qualFlag % force qualitative graphs

lineStyles = set3(1:N)';

else % 10 is a good number to start with the sequential ones.

lineStyles = cmap2linspecer(colorm(N));

end

otherwise % any old case where I need a quick job done.

lineStyles = cmap2linspecer(colorm(N));

end

lineStyles = cell2mat(lineStyles);

end

% extra functions

function varIn = colorBrew2mat(varIn)

for ii=1:length(varIn) % just divide by 255

varIn{ii}=varIn{ii}/255;

end

function varIn = brighten(varIn,varargin) % increase the brightness

if isempty(varargin),

frac = .9;

else

frac = varargin{1};

end

for ii=1:length(varIn)

varIn{ii}=varIn{ii}*frac+(1-frac);

end

function varIn = dim(varIn,f)

for ii=1:length(varIn)

varIn{ii} = f*varIn{ii};

end

function vOut = cmap2linspecer(vIn) % changes the format from a double array to a cell array with the right format

vOut = cell(size(vIn,1),1);

for ii=1:size(vIn,1)

vOut{ii} = vIn(ii,:);

end

% colorm returns a colormap which is really good for creating informative

% heatmap style figures.

% No particular color stands out and it doesn't do too badly for colorblind people either.

% It works by interpolating the data from the

% 'spectral' setting on http://colorbrewer2.org/ set to 11 colors

% It is modified a little to make the brightest yellow a little less bright.

function cmap = colorm(varargin)

n = 100;

if ~isempty(varargin)

n = varargin{1};

end

if n==1

cmap = [0.2005 0.5593 0.7380];

return;

end

if n==2

cmap = [0.2005 0.5593 0.7380;

0.9684 0.4799 0.2723];

return;

end

frac=.95; % Slight modification from colorbrewer here to make the yellows in the center just a bit darker

cmapp = [158, 1, 66; 213, 62, 79; 244, 109, 67; 253, 174, 97; 254, 224, 139; 255*frac, 255*frac, 191*frac; 230, 245, 152; 171, 221, 164; 102, 194, 165; 50, 136, 189; 94, 79, 162];

x = linspace(1,n,size(cmapp,1));

xi = 1:n;

cmap = zeros(n,3);

for ii=1:3

cmap(:,ii) = pchip(x,cmapp(:,ii),xi);

end

cmap = flipud(cmap/255);

end

function cmap = whiteFade(varargin)

n = 100;

if nargin>0

n = varargin{1};