%***********************************************************************
% 3-D FDTD code with PEC boundaries
%***********************************************************************
%
% Program author: Susan C. Hagness
% Department of Electrical and Computer Engineering
% University of Wisconsin-Madison
% 1415 Engineering Drive
% Madison, WI 53706-1691
% 608-265-5739
% hagness@engr.wisc.edu
%
% Date of this version: February 2000
%
% This MATLAB M-file implements the finite-difference time-domain
% solution of Maxwell's curl equations over a three-dimensional
% Cartesian space lattice comprised of uniform cubic grid cells.
%
% To illustrate the algorithm, an air-filled rectangular cavity
% resonator (充气矩形空腔谐振器) is modeled. The length, width, and height of the
% cavity are 10.0 cm (x-direction), 4.8 cm (y-direction), and
% 2.0 cm (z-direction), respectively.
%
% The computational domain is truncated using PEC boundary
% conditions:
% ex(i,j,k)=0 on the j=1, j=jb, k=1, and k=kb planes
% ey(i,j,k)=0 on the i=1, i=ib, k=1, and k=kb planes
% ez(i,j,k)=0 on the i=1, i=ib, j=1, and j=jb planes
% These PEC boundaries form the outer lossless walls of the cavity.
%
% The cavity is excited by an additive current source oriented
% along the z-direction. The source waveform is a differentiated
% Gaussian pulse given by
% J(t)=-J0*(t-t0)*exp(-(t-t0)^2/tau^2),
% where tau=50 ps. The FWHM ( 半最大值全宽度(full width at half maximum))
% spectral bandwidth of this zero-dc-
% content pulse is approximately 7 GHz. The grid resolution (分辨率)
% (dx = 2 mm) was chosen to provide at least 10 samples per
% wavelength up through 15 GHz.
%
% To execute this M-file, type "fdtd3D" at the MATLAB prompt.
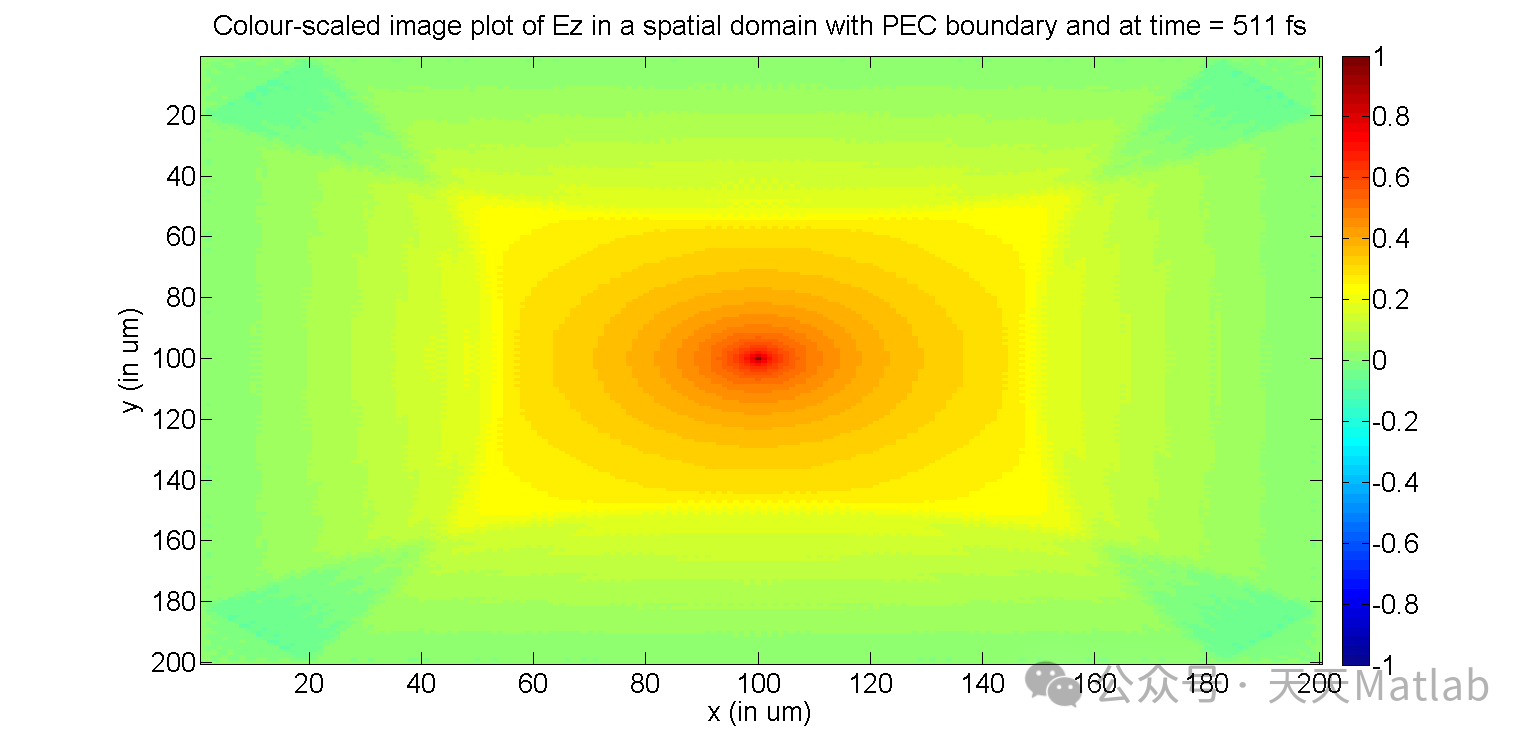
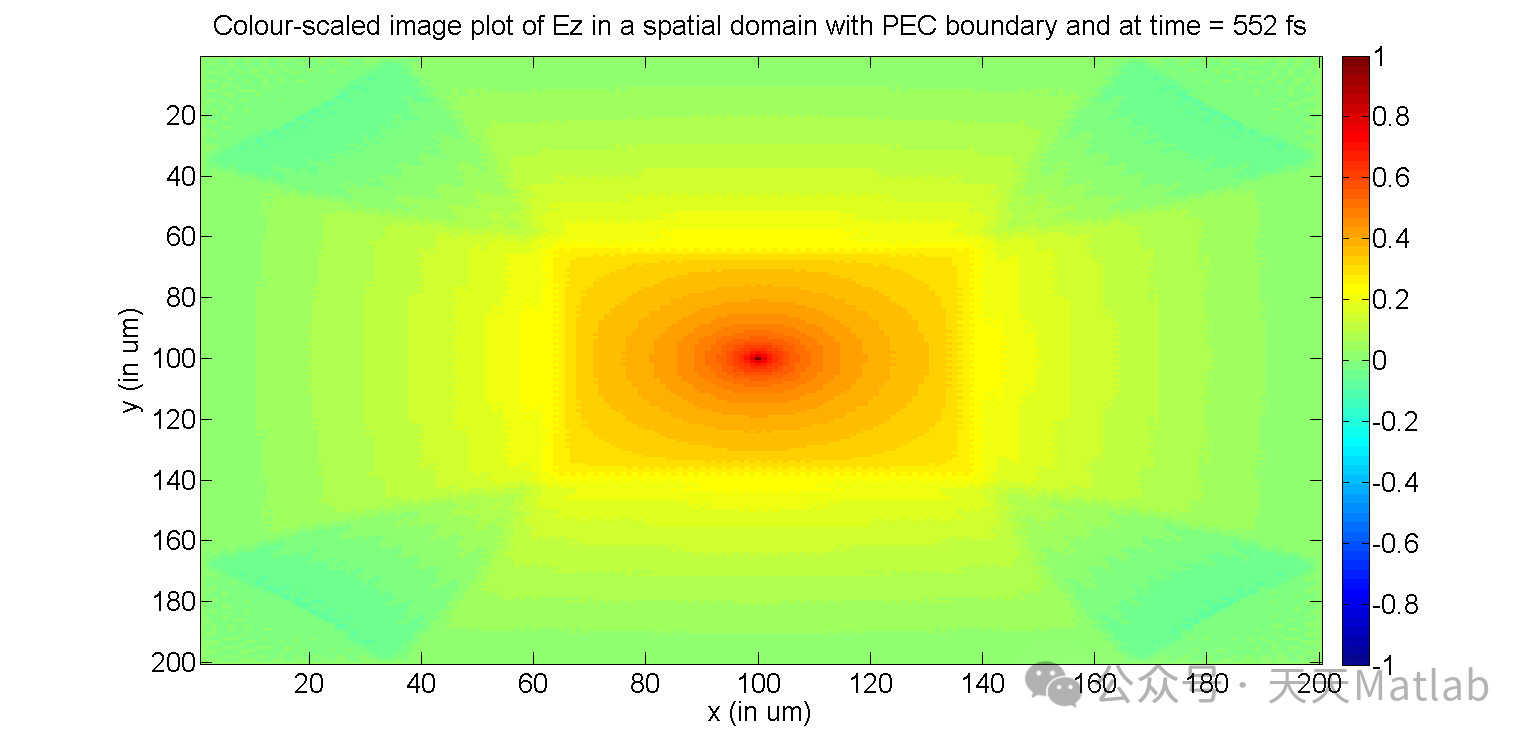
% This M-file displays the FDTD-computed Ez fields at every other
% time step (第一个时间步), and records those frames in a movie matrix, M, which
% is played at the end of the simulation using the "movie" command.
%
%***********************************************************************
clear
%***********************************************************************
% Fundamental constants
%***********************************************************************
cc=2.99792458e8; %speed of light in free space
muz=4.0*pi*1.0e-7; %permeability of free space
epsz=1.0/(cc*cc*muz); %permittivity of free space
%***********************************************************************
% Grid parameters
%***********************************************************************
ie=50; %number of grid cells in x-direction
je=24; %number of grid cells in y-direction
ke=10; %number of grid cells in z-direction
ib=ie+1;
jb=je+1;
kb=ke+1;
is=26; %location of z-directed current source
js=13; %location of z-directed current source
kobs=5;
dx=0.002; %space increment of cubic lattice
dt=dx/(2.0*cc); %time step
nmax=500; %total number of time steps
%***********************************************************************
% Differentiated Gaussian pulse excitation
%***********************************************************************
rtau=50.0e-12;
tau=rtau/dt;
ndelay=3*tau;
srcconst=-dt*3.0e+11;
%***********************************************************************
% Material parameters
%***********************************************************************
eps=1.0; %相对介电常数 epsz,真空介电常数
sig=0.0; %相对电阻率
%***********************************************************************
% Updating coefficients
%***********************************************************************
ca=(1.0-(dt*sig)/(2.0*epsz*eps))/(1.0+(dt*sig)/(2.0*epsz*eps));
cb=(dt/epsz/eps/dx)/(1.0+(dt*sig)/(2.0*epsz*eps));
da=1.0;
db=dt/muz/dx;
%***********************************************************************
% Field arrays
%***********************************************************************
ex=zeros(ie,jb,kb);
ey=zeros(ib,je,kb);
ez=zeros(ib,jb,ke);
hx=zeros(ib,je,ke);
hy=zeros(ie,jb,ke);
hz=zeros(ie,je,kb);
%***********************************************************************
% Movie initialization
%***********************************************************************
tview(:,:)=ez(:,:,kobs);
sview(:,:)=ez(:,js,:);
subplot('position',[0.15 0.45 0.7 0.45]),
pcolor(tview');
%shading flat;
%caxis([-1.0 1.0]);
%colorbar;
%axis image;
title(['Ez(i,j,k=5), time step = 0']);
xlabel('i coordinate');
ylabel('j coordinate');
subplot('position',[0.15 0.10 0.7 0.25]),
pcolor(sview');
%shading flat;
%caxis([-1.0 1.0]);
%colorbar;
%axis image;
title(['Ez(i,j=13,k), time step = 0']);
xlabel('i coordinate');
ylabel('k coordinate');
rect=get(gcf,'Position');
rect(1:2)=[0 0];
M=moviein(nmax/2,gcf,rect);
%***********************************************************************
% BEGIN TIME-STEPPING LOOP
%***********************************************************************
for n=1:nmax
%***********************************************************************
% Update electric fields
%***********************************************************************
ex(1:ie,2:je,2:ke)=ca*ex(1:ie,2:je,2:ke)+...
cb*(hz(1:ie,2:je,2:ke)-hz(1:ie,1:je-1,2:ke)+...
hy(1:ie,2:je,1:ke-1)-hy(1:ie,2:je,2:ke));
ey(2:ie,1:je,2:ke)=ca*ey(2:ie,1:je,2:ke)+...
cb*(hx(2:ie,1:je,2:ke)-hx(2:ie,1:je,1:ke-1)+...
hz(1:ie-1,1:je,2:ke)-hz(2:ie,1:je,2:ke));
ez(2:ie,2:je,1:ke)=ca*ez(2:ie,2:je,1:ke)+...
cb*(hx(2:ie,1:je-1,1:ke)-hx(2:ie,2:je,1:ke)+...
hy(2:ie,2:je,1:ke)-hy(1:ie-1,2:je,1:ke));
ez(is,js,1:ke)=ez(is,js,1:ke)+...
srcconst*(n-ndelay)*exp(-((n-ndelay)^2/tau^2));
% J(t)=-J0*(t-t0)*exp(-(t-t0)^2/tau^2)
%***********************************************************************
% Update magnetic fields
%***********************************************************************
hx(2:ie,1:je,1:ke)=hx(2:ie,1:je,1:ke)+...
db*(ey(2:ie,1:je,2:kb)-ey(2:ie,1:je,1:ke)+...
ez(2:ie,1:je,1:ke)-ez(2:ie,2:jb,1:ke));
hy(1:ie,2:je,1:ke)=hy(1:ie,2:je,1:ke)+...
db*(ex(1:ie,2:je,1:ke)-ex(1:ie,2:je,2:kb)+...
ez(2:ib,2:je,1:ke)-ez(1:ie,2:je,1:ke));
hz(1:ie,1:je,2:ke)=hz(1:ie,1:je,2:ke)+...
db*(ex(1:ie,2:jb,2:ke)-ex(1:ie,1:je,2:ke)+...
ey(1:ie,1:je,2:ke)-ey(2:ib,1:je,2:ke));
%***********************************************************************
% Visualize fields
%***********************************************************************
if mod(n,2)==0;
timestep=int2str(n);
tview(:,:)=ez(:,:,kobs);
sview(:,:)=ez(:,js,:);
subplot('position',[0.15 0.45 0.7 0.45]),
pcolor(tview');
% shading flat;
% caxis([-1.0 1.0]);
% colorbar;
% axis image;
title(['Ez(i,j,k=5), time step = ',timestep]);
xlabel('i coordinate');
ylabel('j coordinate');
subplot('position',[0.15 0.10 0.7 0.25]),
pcolor(sview');
% shading flat;
% caxis([-1.0 1.0]);
% colorbar;
% axis image;
title(['Ez(i,j=13,k), time step = ',timestep]);
xlabel('i coordinate');
ylabel('k coordinate');
nn=n/2;
M(:,nn)=getframe(gcf,rect);
end;
%***********************************************************************
% END TIME-STEPPING LOOP
%***********************************************************************
end
movie(gcf,M,0,10,rect);




















 1922
1922

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








