【卡尔曼追踪】Vold-Kalman 阶次追踪（Matlab实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

一、基本原理

Volterra-Kalman 阶次追踪融合了 Volterra 级数展开与 Kalman 滤波的优势。Volterra 级数能够以多项式形式描述非线性系统的输入输出关系，将复杂的非线性动态特性分解为不同阶次的子系统响应之和，从而揭示系统内在的非线性结构。而 Kalman 滤波作为一种强大的状态估计方法，擅长处理系统中的噪声干扰，实时追踪系统状态的变化。二者结合，通过 Volterra 级数构建系统的非线性模型框架，利用 Kalman 滤波依据系统观测值对模型参数进行迭代优化，实现对非线性系统阶次的精准追踪。

二、应用场景

1. 通信系统：在无线通信中，信号常受到信道非线性失真的影响，如功率放大器的非线性特性会导致信号畸变。Volterra-Kalman 阶次追踪可对信道的非线性特性进行建模与跟踪，辅助接收机准确还原发送信号，提升通信质量，降低误码率。 2. 机械故障诊断：旋转机械在运行过程中，部件的磨损、松动等故障往往引发非线性的振动特性变化。运用该技术，能实时追踪振动信号的非线性阶次变化，及时发现潜在故障隐患，为预防性维护提供依据，保障设备可靠运行。 3. 生物医学信号处理：例如脑电图（EEG）、心电图（ECG）等生物电信号，本身蕴含复杂的生理信息且具有非线性特征。Volterra-Kalman 阶次追踪有助于提取信号中的关键特征，辅助医生诊断神经系统疾病、心血管疾病等，推动精准医疗发展。

三、优势

1. 强大的非线性处理能力：相较于传统线性建模方法，它能深入剖析系统的非线性行为，精准捕捉系统在不同工况下的动态变化，提供更贴合实际的系统描述。 2. 实时性与适应性：Kalman 滤波的递推特性使其具备实时更新系统状态估计的能力，能够快速适应系统运行过程中的参数漂移、外界干扰等变化，确保阶次追踪的准确性与及时性。 3. 噪声抑制：有效滤除观测数据中的噪声成分，避免噪声对系统阶次判断的干扰，使提取的系统特征更加可靠，提高后续分析与决策的质量。

四、挑战与限制

1. 计算复杂度：由于 Volterra 级数展开涉及高维多项式运算，尤其在处理高阶非线性系统时，计算量呈指数级增长，对计算硬件提出较高要求，限制了其在一些实时性要求极高、资源受限场景下的应用。 2. 模型参数辨识难度：准确辨识 Volterra 级数中的大量参数是关键但棘手的问题，不当的参数初始化或不充分的数据样本可能导致模型收敛缓慢甚至不收敛，影响追踪效果。 3. 对先验知识的依赖：在构建模型时，通常需要一定的系统先验知识，如大致的非线性阶次范围、噪声统计特性等，若先验信息不准确，会给实际应用带来困难。

五、发展趋势

随着计算技术的飞速进步，如 GPU 并行计算、量子计算的逐步探索应用，有望缓解计算复杂度难题，拓展 Volterra-Kalman 阶次追踪的适用范围。同时，与深度学习等新兴技术融合，借助深度学习强大的自动特征提取能力优化模型参数辨识过程，进一步提升其在复杂系统中的性能表现，为更多领域的科学研究与工程实践注入新活力。 综上所述，Volterra-Kalman 阶次追踪以其独特的技术优势在多个领域展现出广阔应用前景，尽管面临挑战，但持续的技术创新将助力其克服困难，实现更大价值。

📚2 运行结果

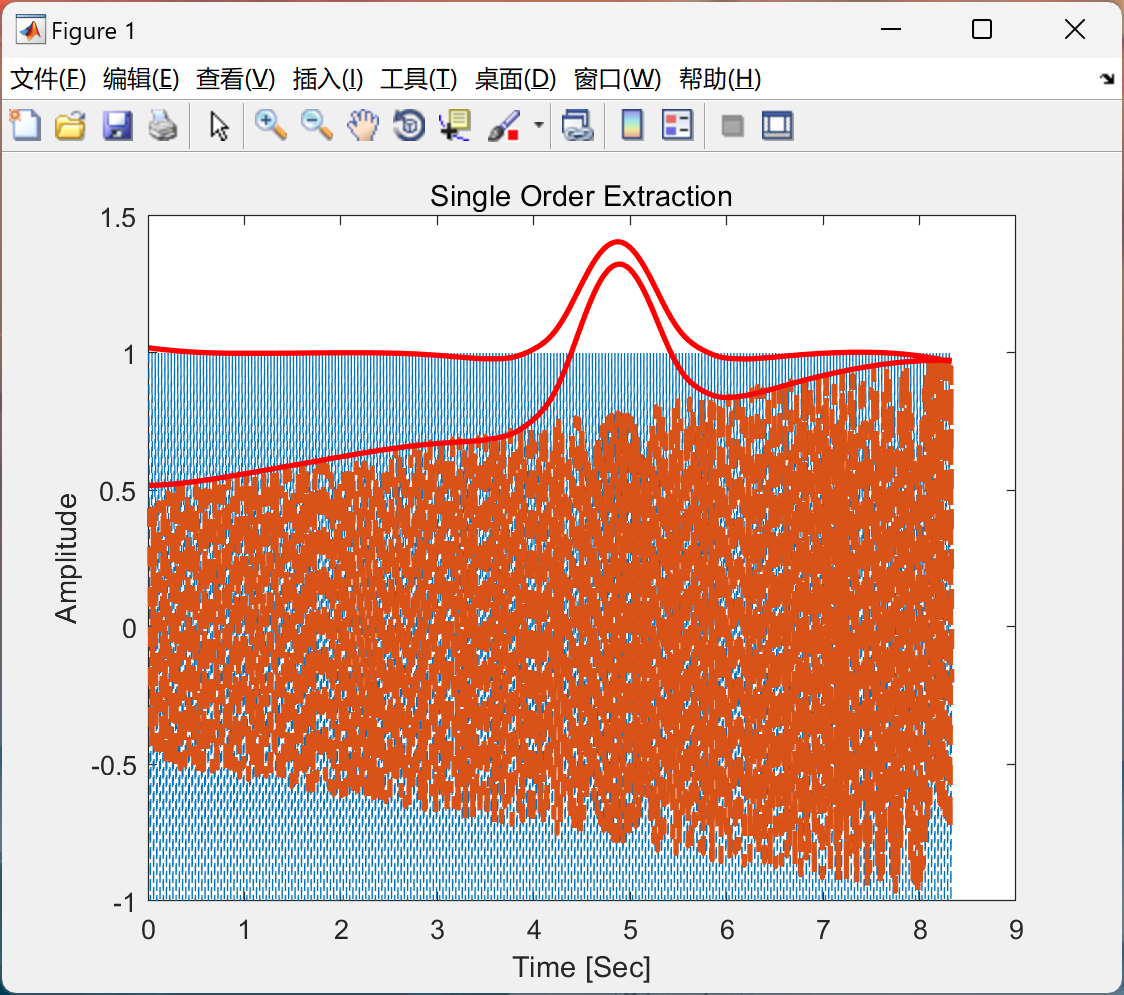
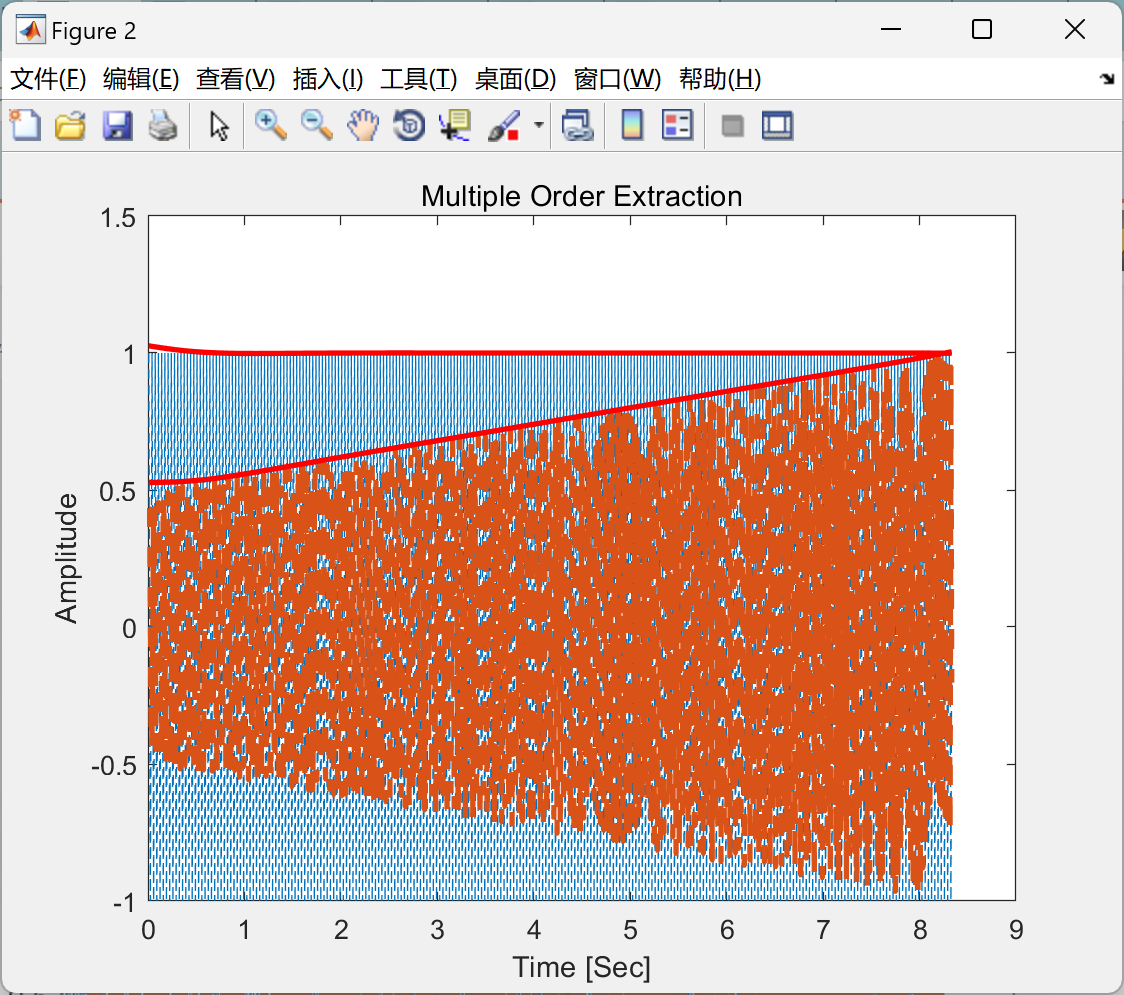
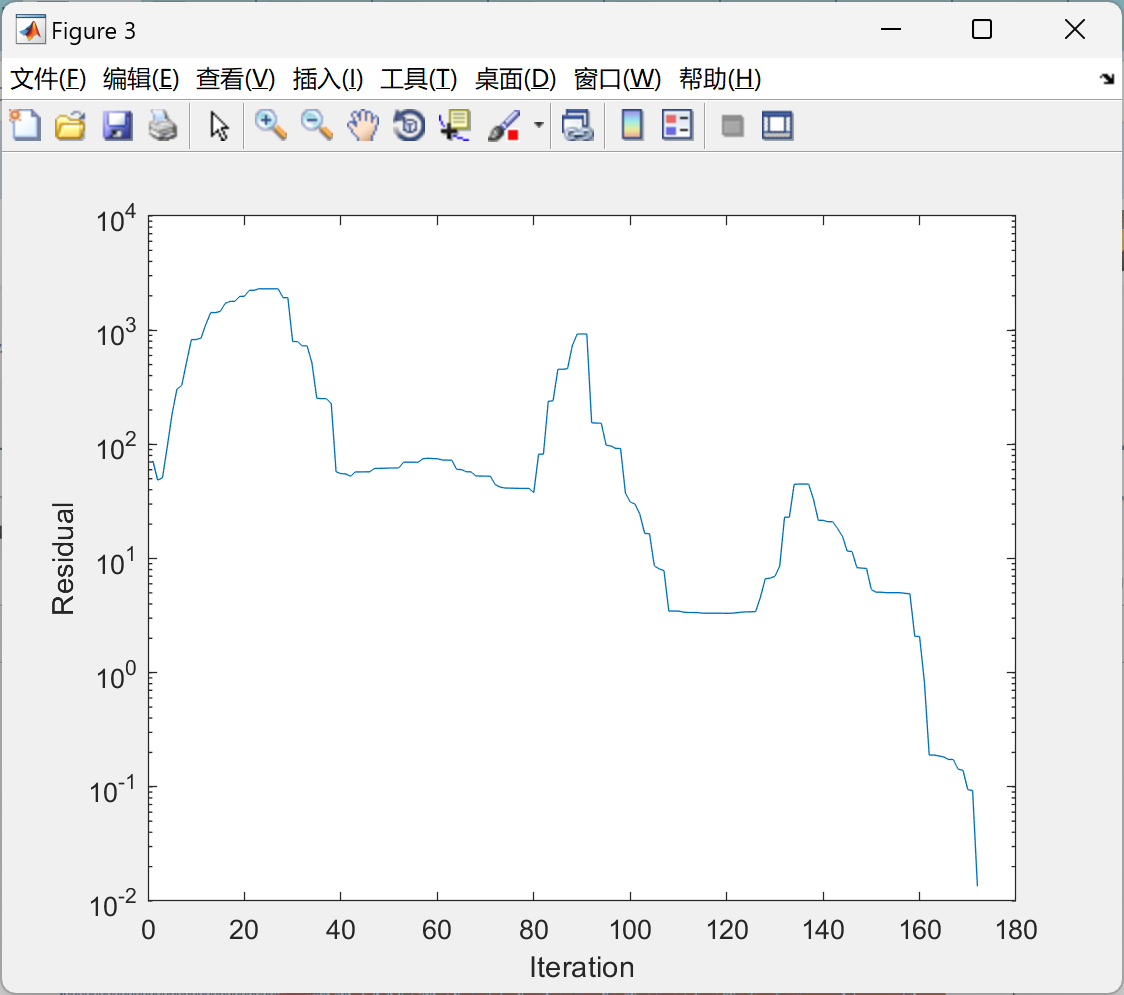
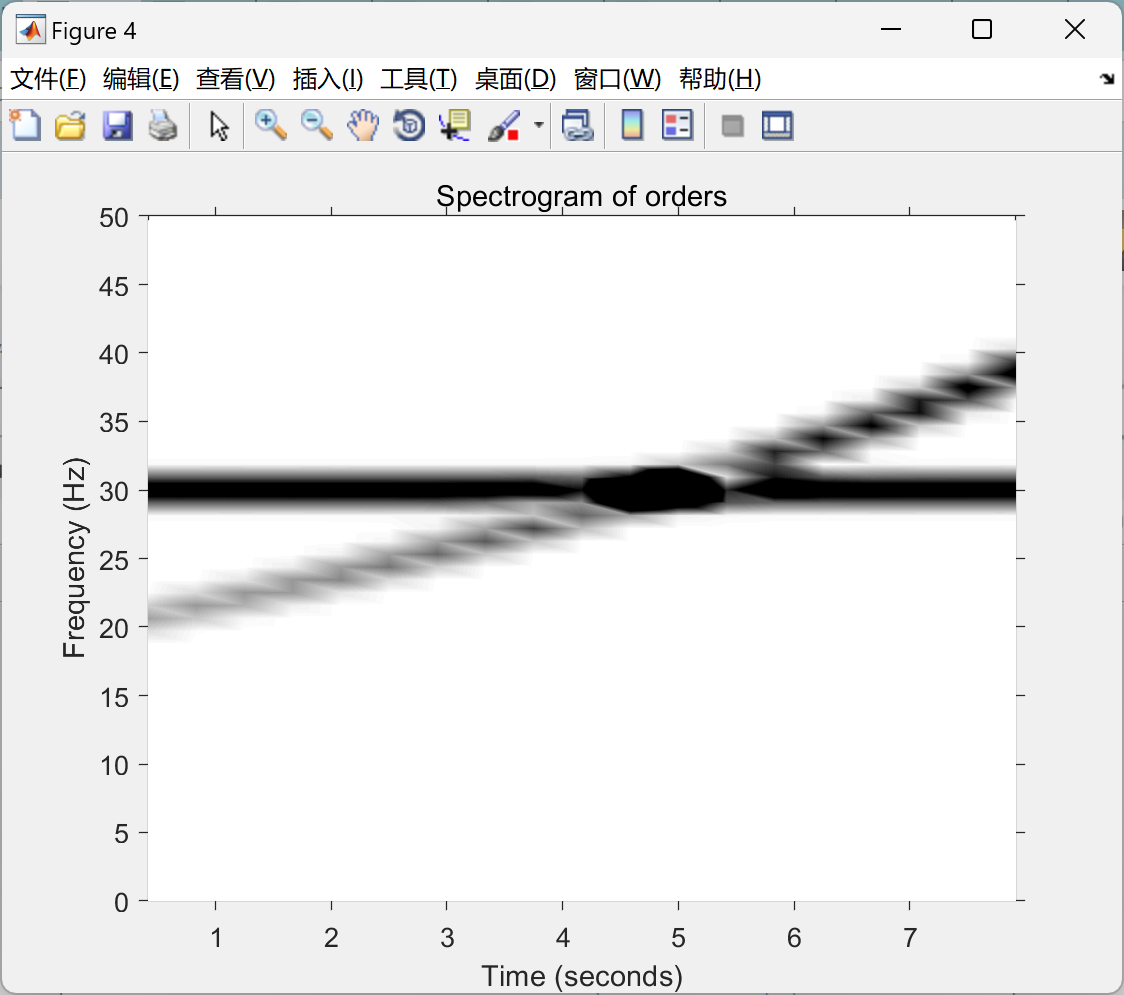
部分代码：

clear;
%
addpath '..';
%
fs=100;
nt=1000;
t=[1:nt]./fs;t=t(:);
%
f0=1.5;f1=10/2.15;
opm=log2(f1/f0)*60/t(end);
fup=f0*2.^(opm/60*t);fup=fup(:);
%
f0=10-(10-1.5)/2;f1=10;
inc=(f1-f0)/nt;
fdn=[f1:-inc:f0+inc];fdn=fdn(:);
%
f=0.75/t(end);
am1=0.25*sin(2*pi*f*t-pi/4);am1=am1+0.75;
am2=0.25*sin(2*pi*f*t-pi/1.7);am2=am2+0.75;
am3=0.25*sin(2*pi*f*t-pi/8);am3=am3+0.75;
am4=0.25*sin(2*pi*f*t-pi/2.5);am4=am4+0.75;
am5=0.25*sin(2*pi*f*t-pi/5);am5=am5+0.75;
am6=0.25*sin(2*pi*f*t-pi/10);am6=am6+0.75;
%
x1=am1.*sin(1*2*pi*cumsum(fup/fs));x1=x1./std(x1);
x2=am2.*sin(2*2*pi*cumsum(fup/fs));x2=x2./std(x2);
x3=am3.*sin(3*2*pi*cumsum(fup/fs));x3=x3./std(x3);
x4=am4.*sin(1*2*pi*cumsum(fdn/fs));x4=x4./std(x4);
x5=am5.*sin(2*2*pi*cumsum(fdn/fs));x5=x5./std(x5);
x6=am6.*sin(3*2*pi*cumsum(fdn/fs));x6=x6./std(x6);
%
fp=[fdn,2*fup,fup];
xp=[x4,x2,x1];
[nt,nch]=size(xp);
%
nsens=1;
%A=randn(nsens,nch);
A=[1,1,1];
%
xe=(A*xp.').';
xc=A(ones(nt,1),:).*xp;
%
%xe=xe+0.05*randn(nt,nsens); % add noise

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]陈剑雨,董广明,陈进,等.基于Vold-Kalman阶次提取的非平稳声源定位方法[J].噪声与振动控制,2021,41(04):27-34.

[2]罗志鹏.基于阶次跟踪的变转速齿轮箱故障诊断方法研究[D].河南理工大学,2019.DOI:10.27116/d.cnki.gjzgc.2019.000059.

🌈4 Matlab代码实现