【卡尔曼滤波器】卡尔曼滤波器与线性动态系统（Matlab实现）

最新推荐文章于 2025-06-01 11:16:27 发布

荧光Matlab

最新推荐文章于 2025-06-01 11:16:27 发布

阅读量739

点赞数 13

CC 4.0 BY-SA版权

文章标签： matlab 开发语言

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/146077045

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

卡尔曼滤波器与线性动态系统概述在现代工程、控制科学以及信号处理等众多领域，卡尔曼滤波器与线性动态系统紧密相连，为解决复杂的状态估计与系统控制问题提供了关键的理论支撑与实用工具。

一、应用领域

1. 导航系统：在卫星导航、惯性导航等场景，传感器测量值（如 GPS 坐标、加速度计读数等）存在噪声，卡尔曼滤波器将来自不同传感器的信息融合，精确估计载体（飞机、船舶、汽车等）的位置、速度、姿态等状态，实现精准导航，保障航行安全。 2. 工业自动化：对于工业机器人、自动化生产线设备，卡尔曼滤波器依据电机编码器、力传感器等反馈，实时跟踪机械部件的运动状态，补偿控制误差，确保高精度作业，提升生产效率与产品质量。 3. 目标跟踪：在军事侦察、安防监控领域，雷达、光学相机等传感器探测目标，卡尔曼滤波器利用目标的运动模型，从嘈杂的观测信号中持续追踪目标轨迹，预判目标动向，为决策提供有力支持。

二、优势特点

1. 实时性强：采用递推算法，无需存储大量历史数据，能随着新观测值实时更新状态估计，迅速适应系统变化，满足实时系统对快速响应的要求。 2. 最优估计：在给定线性动态系统模型及噪声统计特性假设下，卡尔曼滤波器提供理论上的最优线性无偏估计，使估计误差的方差在各时刻达到最小，确保估计的准确性与可靠性。 3. 可处理多传感器融合：轻松整合多种类型、不同精度的传感器数据，通过合理设置观测方程，将各传感器优势互补，充分挖掘观测信息，提升系统整体性能。

三、局限性与挑战

1. 对模型准确性的依赖：若线性动态系统的状态方程或观测方程建模不准确，如实际系统存在非线性特性却强行用线性模型近似，卡尔曼滤波器性能会大幅下降，甚至得出错误的状态估计。 2. 噪声特性假设要求严格：需要精确已知过程噪声与观测噪声的协方差矩阵，实际应用中噪声统计特性往往难以精确测定，若估计偏差较大，同样影响滤波器效果。 3. 计算复杂度：在高维系统或复杂模型下，卡尔曼滤波器涉及大量矩阵运算，计算成本较高，对计算设备性能有一定要求，限制了其在资源受限场景的应用。

四、发展趋势

面对局限性，研究人员不断探索改进方向。一方面，针对非线性系统，发展出扩展卡尔曼滤波器、 unscented 卡尔曼滤波器等变体，通过不同方式处理非线性，拓展卡尔曼滤波家族应用范围；另一方面，结合新兴技术如机器学习，利用数据驱动方法自适应学习模型参数与噪声特性，减少对先验知识的依赖，提升卡尔曼滤波器在复杂多变环境下的自适应能力，使其持续赋能现代科技发展。综上所述，卡尔曼滤波器与线性动态系统相辅相成，前者依托后者模型实现卓越的状态估计功能，广泛应用于诸多领域，虽存在挑战，但发展前景依然广阔，持续推动各行业的智能化进程。

📚2 运行结果

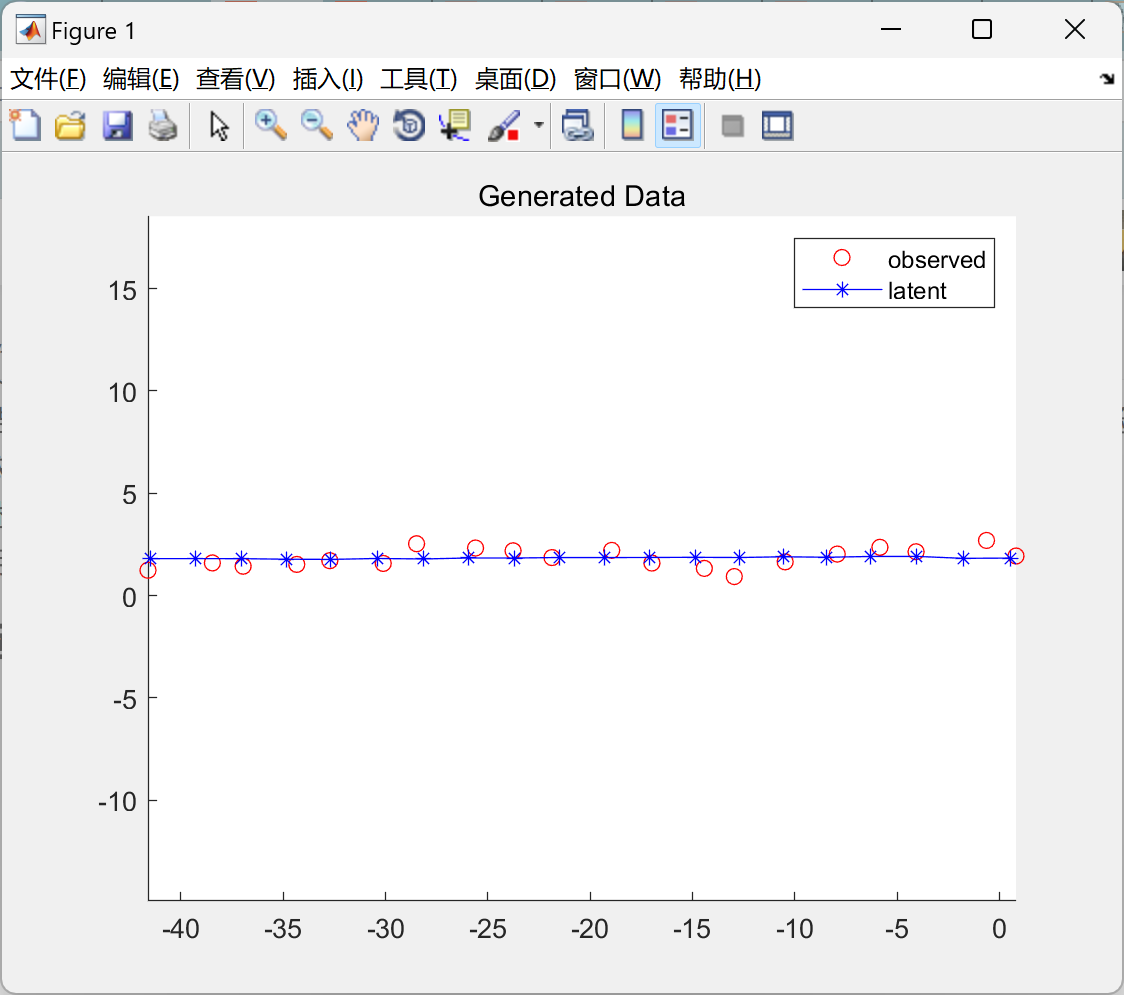
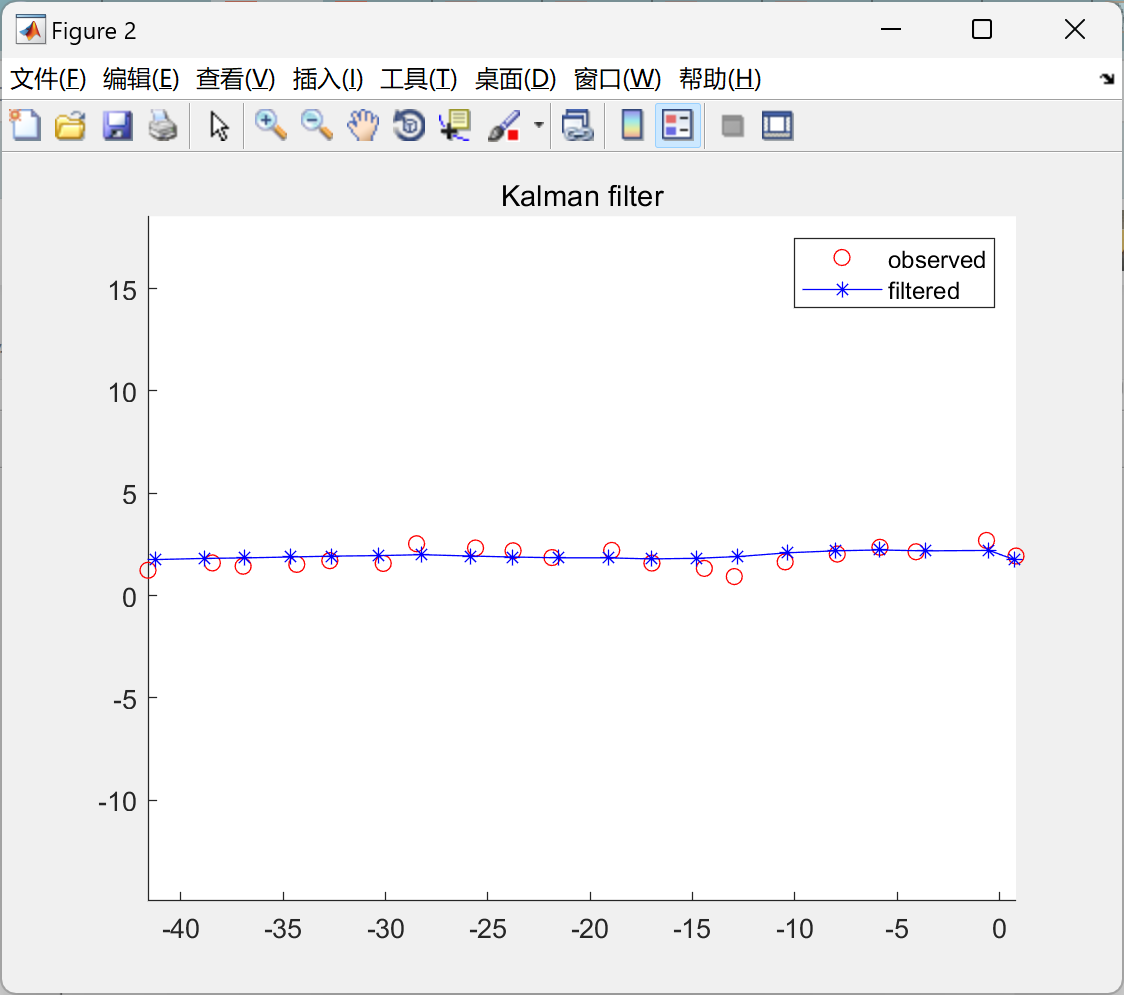
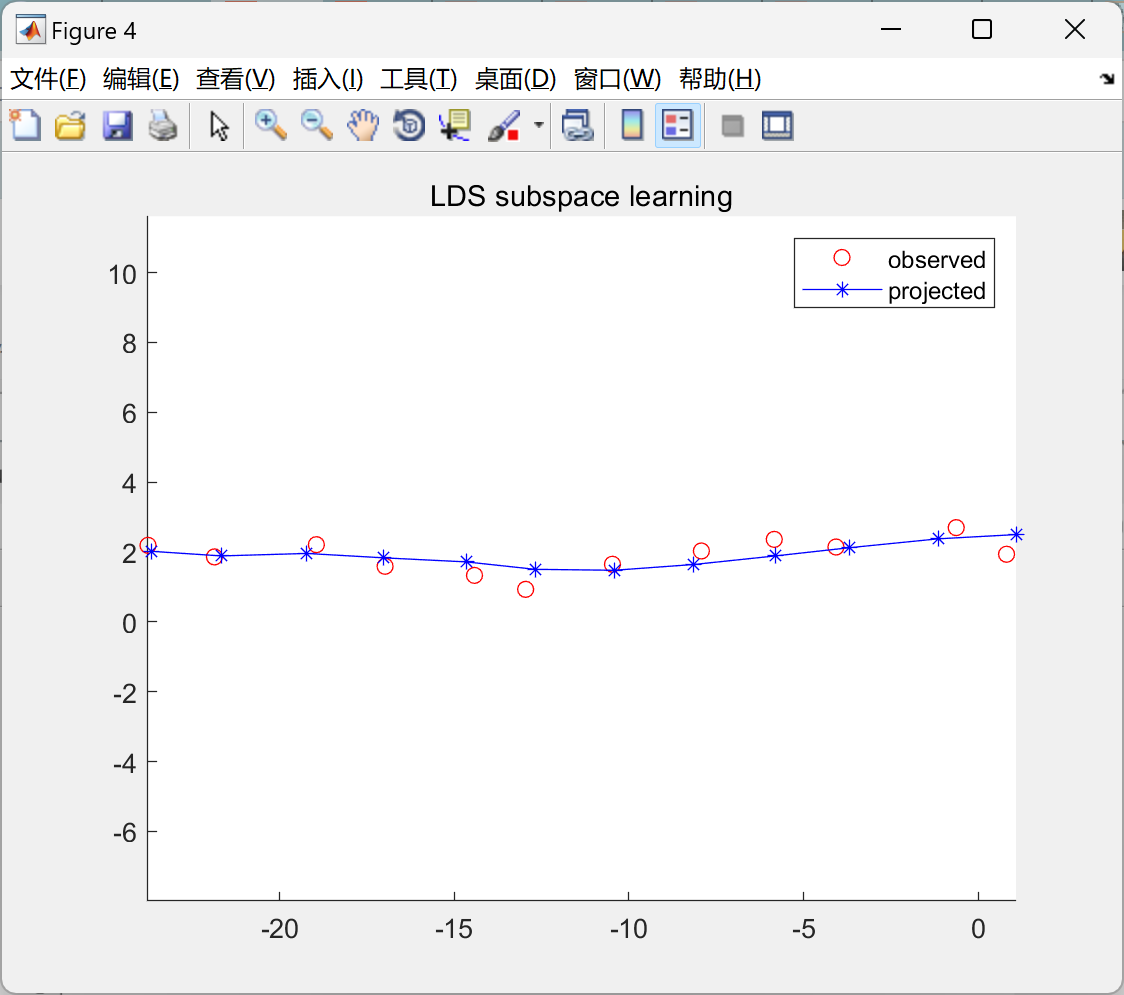
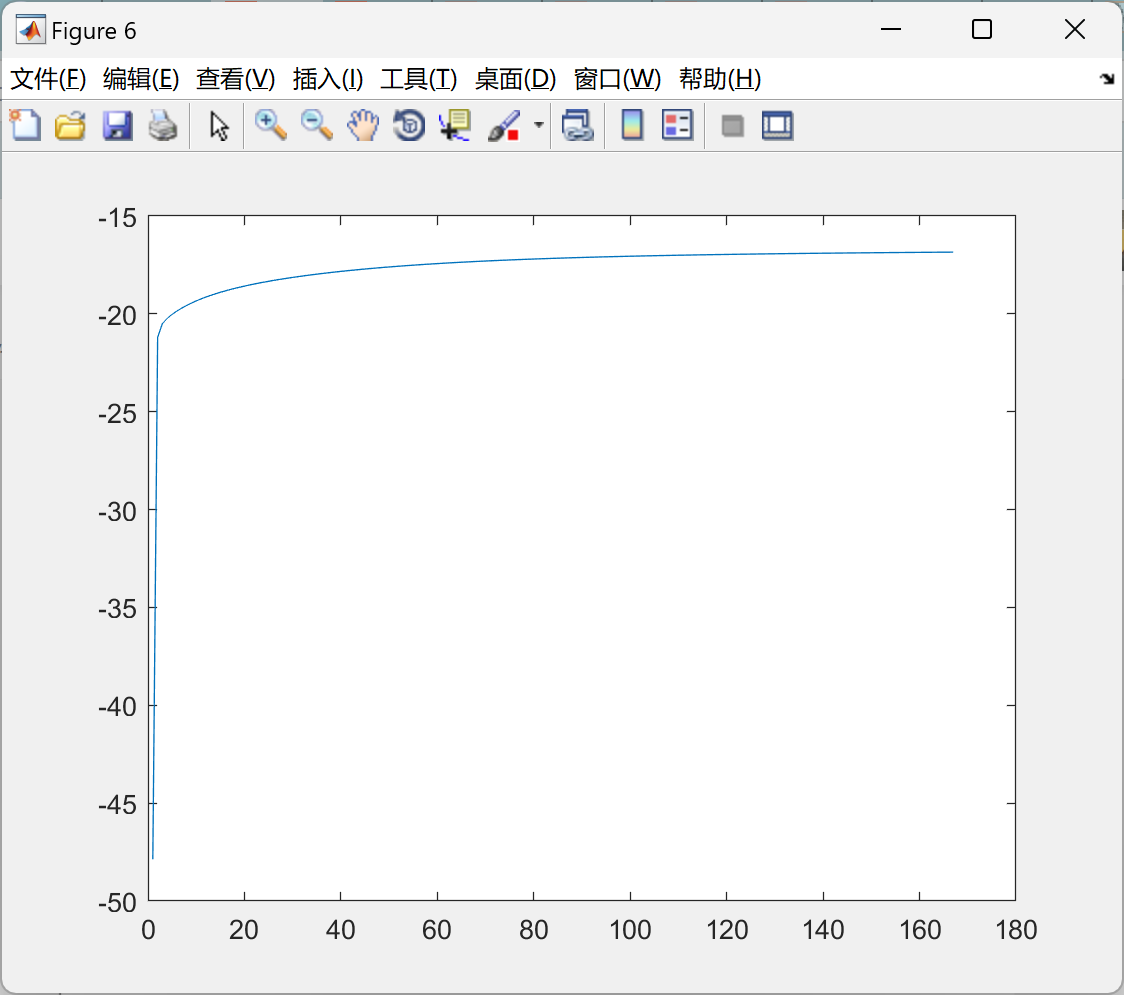
部分代码：

close all;
% Parameter
clear; 
d = 2;
k = 3;
n = 20;

A = [1,0,1; 
     0 1,0;
     0,0,1];
G = eye(k)*1e-3;
 
C = [1,0,0;
     0 1,0];
S = eye(d)*1e-1;

mu0 = [0;0;0];
P0 = eye(k);

model.A = A;
model.G = G;
model.C = C;
model.S = S;
model.mu0 = mu0;
model.P0 = P0;

%% Generate data
[z,x] = ldsRnd(model,n);
figure;
hold on
plot(x(1,:), x(2,:), 'ro');
plot(z(1,:), z(2,:), 'b*-');
legend('observed', 'latent')
title('Generated Data')
axis equal
hold off
%% Kalman filter
[mu, V, llh] = kalmanFilter(model,x);
figure
hold on
plot(x(1,:), x(2,:), 'ro');
plot(mu(1,:), mu(2,:), 'b*-');
legend('observed', 'filtered')
title('Kalman filter')
axis equal
hold off
%% Kalman smoother
[nu, U, llh] = kalmanSmoother(model,x);
figure
hold on
plot(x(1,:), x(2,:), 'ro');
plot(nu(1,:), nu(2,:), 'b*-');
legend('observed', 'smoothed')
title('Kalman smoother')
axis equal
hold off
%% LDS Subspace