【控制】 LQR 和强化学习的结合（Matlab实现）

最新推荐文章于 2025-04-27 13:16:16 发布

荧光Matlab

最新推荐文章于 2025-04-27 13:16:16 发布

阅读量679

点赞数 9

CC 4.0 BY-SA版权

文章标签： matlab 开发语言

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/145911244

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、引言

在控制领域，线性二次型调节器（LQR）与强化学习（RL）是两种极具影响力的方法。LQR 凭借其成熟的理论基础，能针对线性系统，基于给定的二次型性能指标，高效求解最优控制策略，实现系统稳定与优化。强化学习则模拟生物从环境交互中学习的模式，通过智能体不断试错，依据奖励反馈来学习最优行为策略，以适应复杂多变的环境。当二者结合，有望融合 LQR 的精准高效与强化学习的灵活应变，为解决复杂系统控制问题开辟新路径。

二、结合方式与优势

初始化与引导：利用 LQR 为强化学习提供初始策略。对于复杂系统，强化学习从零开始学习策略耗时久，LQR 的最优控制律可作为初始策略，智能体基于此在环境中微调，加速学习进程。例如在机器人路径规划中，LQR 给出基本稳定路径，强化学习再优化避开动态障碍。
约束与优化：结合 LQR 的性能指标优化强化学习目标。强化学习追求奖励最大化，有时会忽视控制成本，引入 LQR 的二次型指标，能在优化奖励时兼顾控制能量消耗等因素，实现更平衡的控制。像无人机飞行控制，既保障飞行任务完成，又节省能源。
模型融合：构建混合模型架构。部分状态空间用 LQR 精确控制，复杂、不确定部分交给强化学习应对。如工业自动化生产线，设备常规运行由 LQR 维持，故障突发、工况剧变时，强化学习介入调整，提升系统整体可靠性。

三、应用领域

自动驾驶：车辆纵向控制结合 LQR 稳定车速，强化学习应对复杂路况如超车、避障，优化驾驶策略，提升行车安全性与舒适性。
机器人控制：机器人关节运动，LQR 保障基础动作精准，强化学习助力适应不同任务、抓取不规则物体，拓展机器人作业能力。
智能电网：电网频率调节，LQR 维持日常稳定，强化学习在用电高峰、故障冲击下灵活调配资源，保障供电可靠性。

四、挑战与展望

虽二者结合前景广阔，但挑战并存。一方面，二者融合的理论体系尚不完善，参数协调、模型切换等机制需深入研究；另一方面，计算复杂度高，尤其在大规模系统，实时性要求难以满足。未来，随着算法优化、硬件算力提升，LQR 与强化学习结合有望攻克难题，在更多前沿领域，如深空探测、生物医疗等，发挥关键控制效能，推动科技进步。

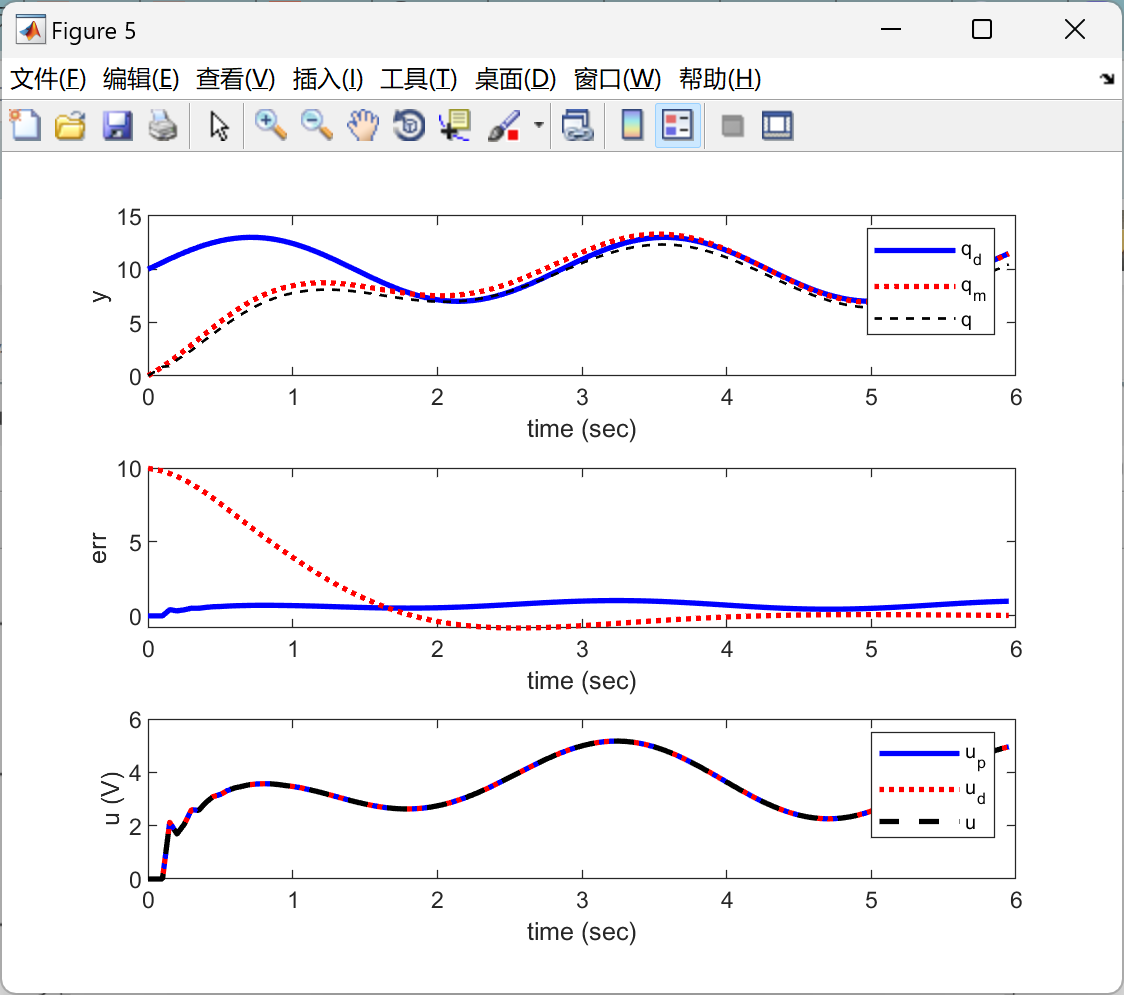
📚2 运行结果

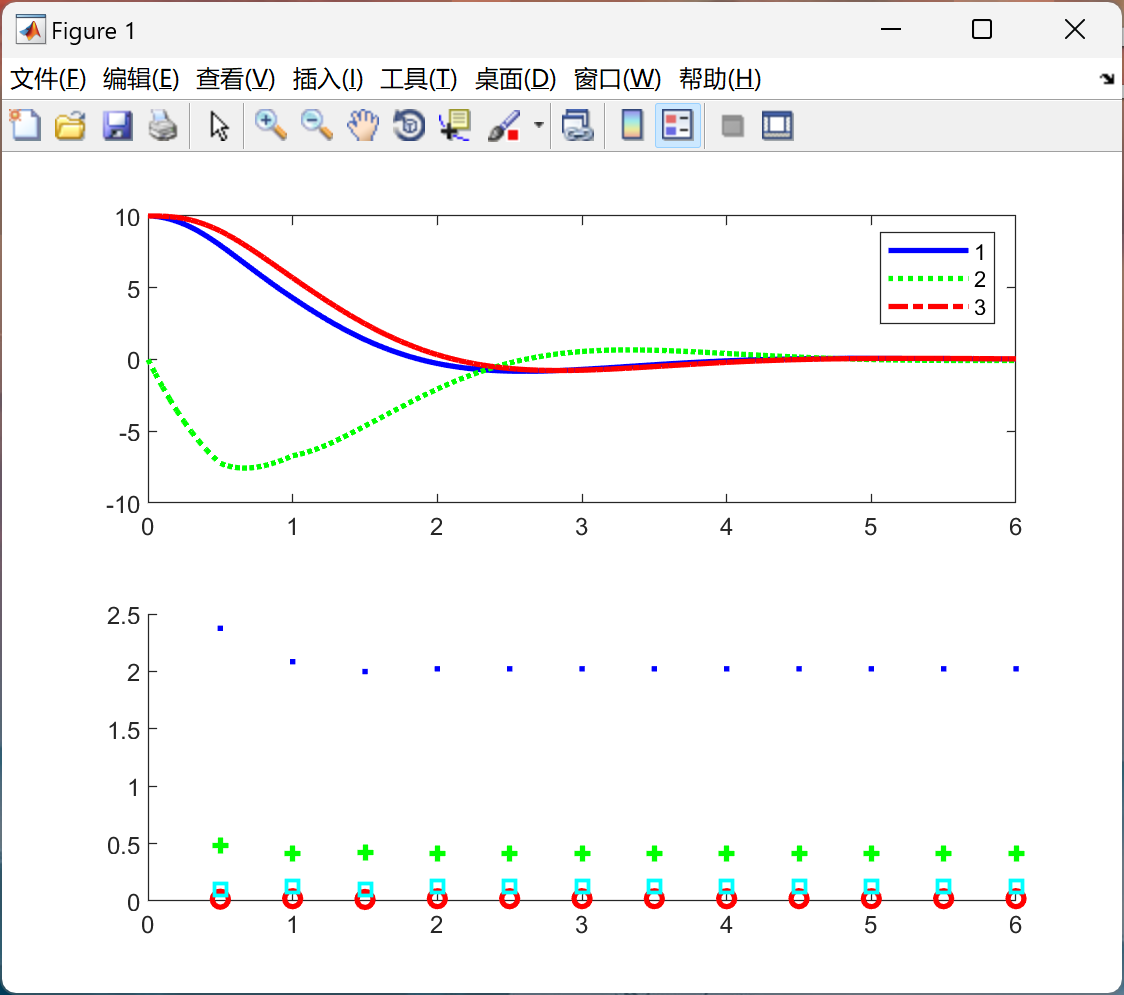
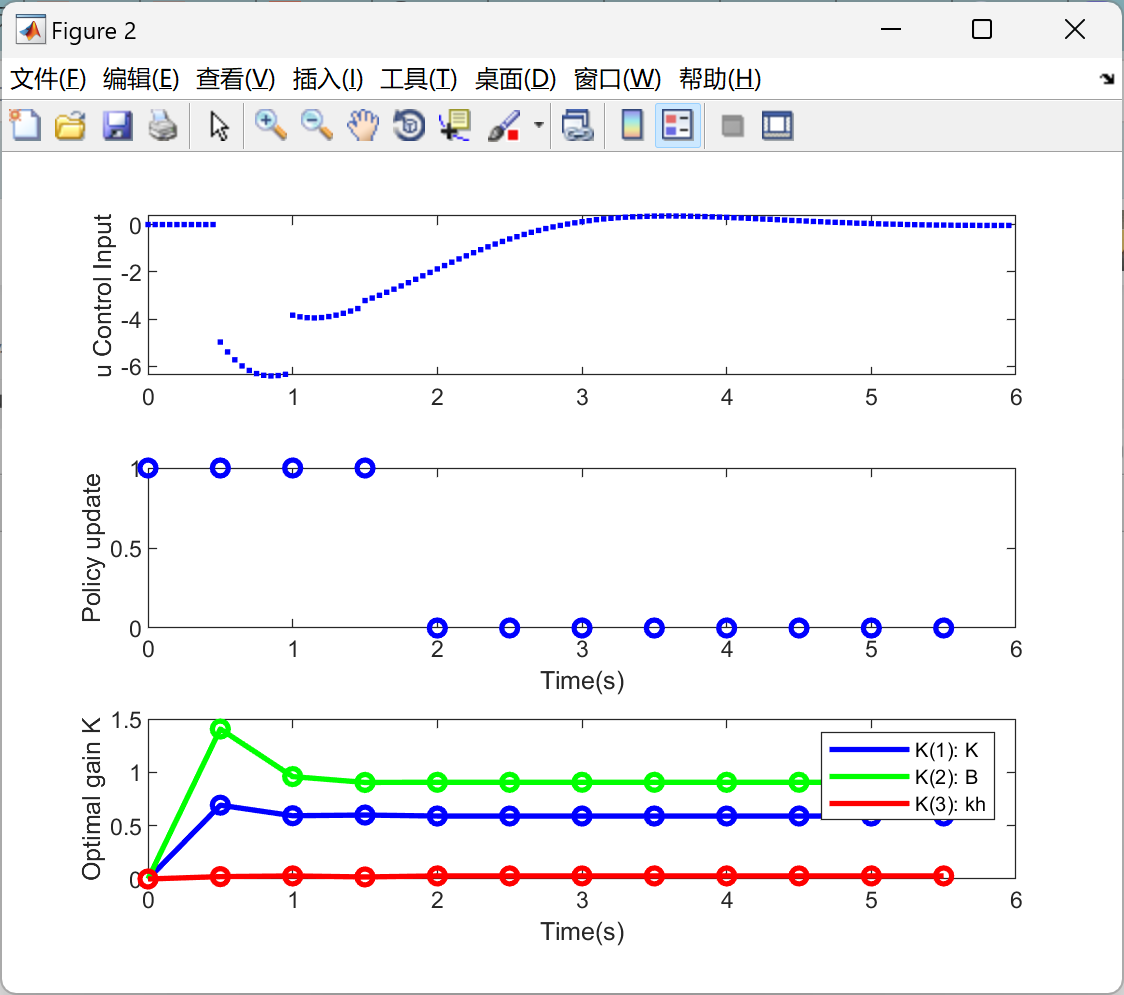
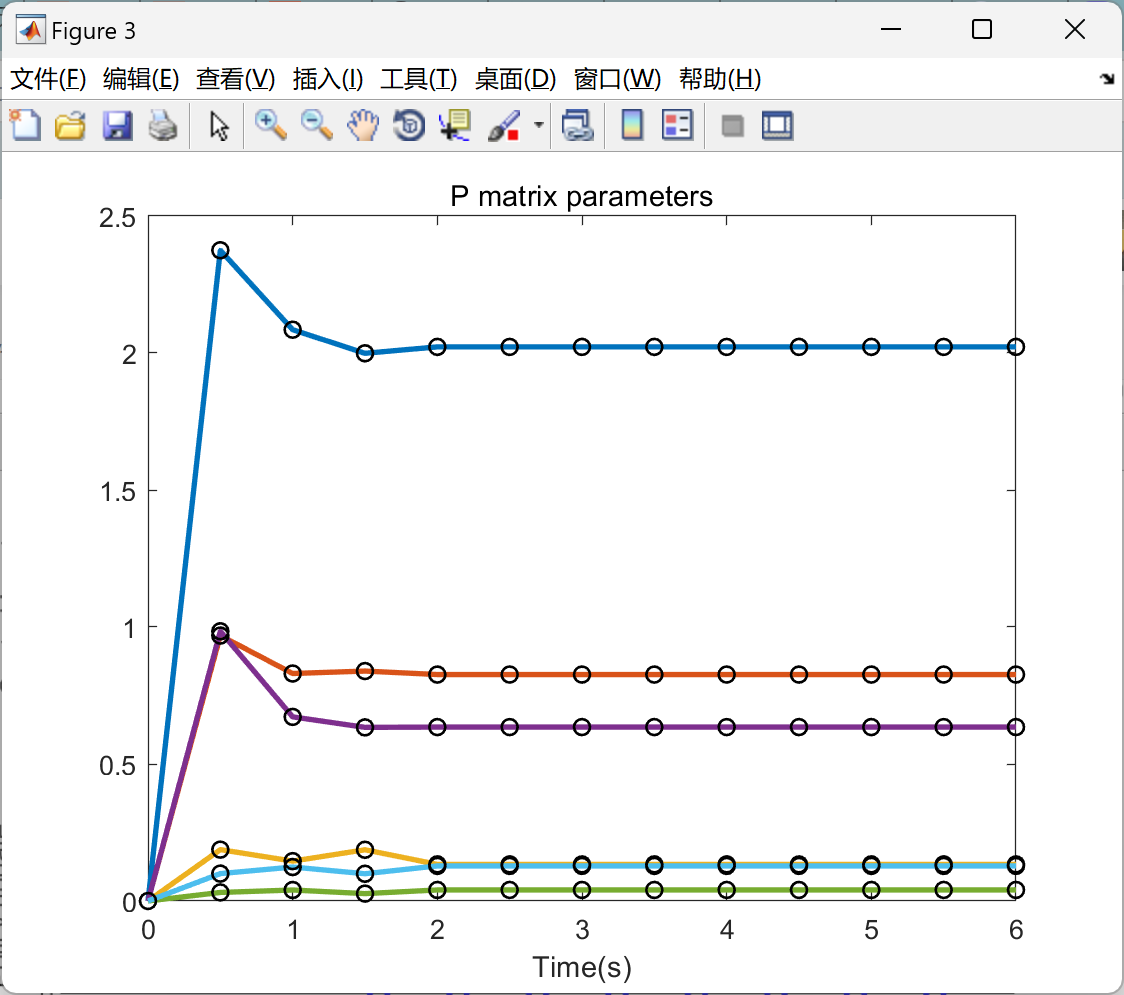
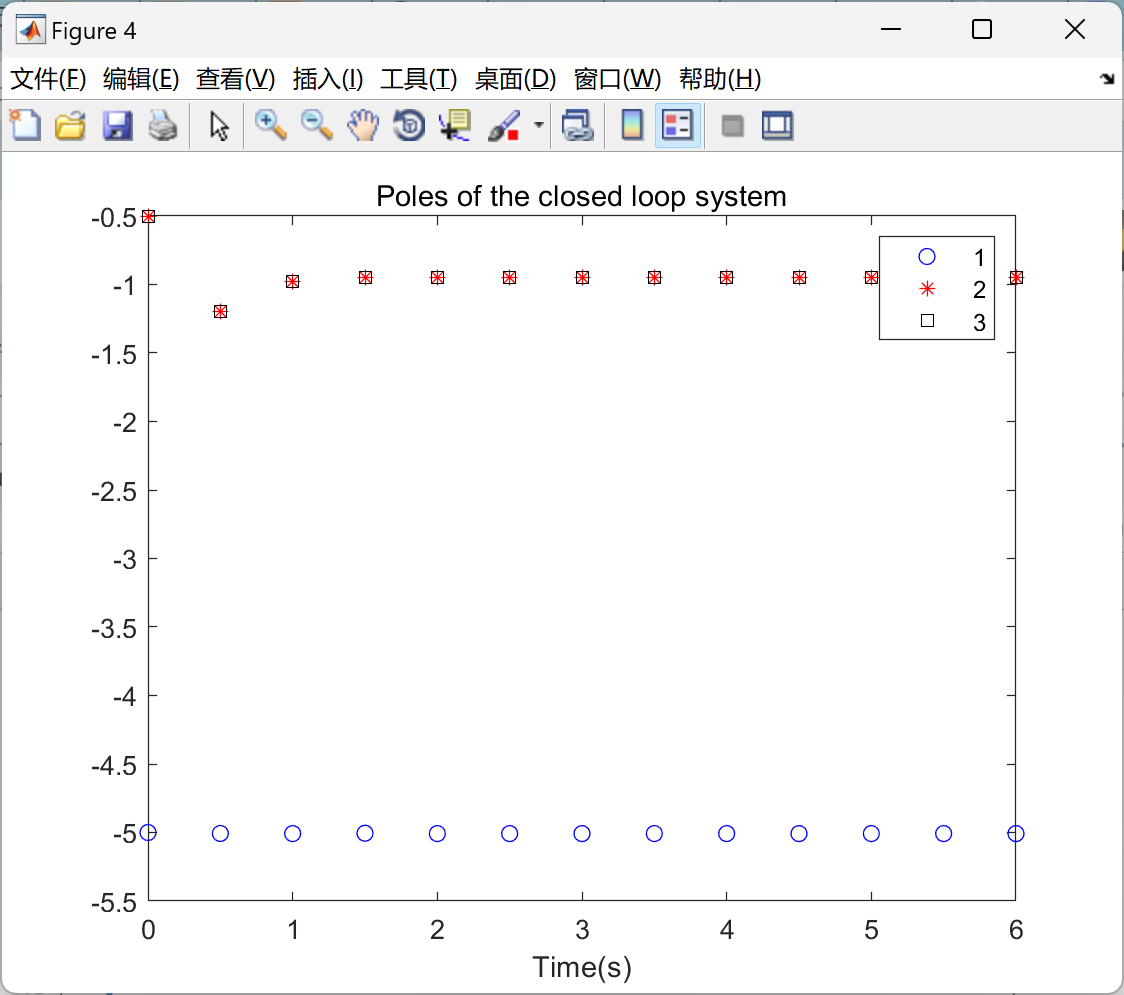
主函数部分代码：

clear all;close all;clc;

%% Initialization
global P u T Tfinal epsilon A B C R HH  C1 C2
global zero_G pole_G gain_G ke kd kp wn ode_k noise

% sample time
T=0.05; Tfinal = 6;
N=Tfinal/T; % Length of the simulation in samples
epsilon = 0.00000001; % For the converge
R = 0.7;
HH = 10; % Period of update policy

%system matrix
zero_G = []; pole_G = [-5]; gain_G = 5; % Human's model (zero, pole, gain)
G_fh = zpk(zero_G,pole_G,gain_G); [num, den] = tfdata(G_fh, 'v'); 
ke = num(2); kp = den(2); kd = den(1); % Human's parameter

wn = 1; % Natural frequency
A = [0         1          0;       % System matrix
     -2*wn     -wn^2       0;
%      0     0       0;
     ke/kd     0          -kp/kd]; 
B = -[0; 1; 0];                     % Input matrix

C = [1 0 0];

eig_A = eig(A)


%initial conditions
x0_set = [10,0,10,0]
x0=x0_set; % 3 vectors and J
P=[0 0 0;
   0 0 0; 
   0 0 0]; % Positive definite and symmetric matrix P
Pold = eye(3);  Psave = zeros(length(P),length(P),2);  % For monitoring P matrix
uu=[];       % saving the control signal for plot
xx=[];       % saving the state for plot
KK=[];       % saving the optimal gain for plot

% Vectorization: Parameters returned by the least squares
WW=[P(1,1); 2*P(1,2); 2*P(1,3); P(2,2); 2*P(2,3); P(3,3)];
WWP=[WW; 0];

% Parameters for the batch least squares
j=0; Xpi=[];
E=real(eig(A-B*inv(R)*B'*P)); % saves the poles of the closed loop system
EE = [E];
upd=[];                   % stores information relative to updates the parameters
k=1; ch=0;                 % Real time iteration, Interval iteration
qm = zeros(10,1);
qd = zeros(10,1); qd(1) = x0_set(1);