【机器人路径规划】移动机器人路径规划的实现（Matlab实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/145922473

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

移动机器人在当今社会的众多领域正发挥着日益重要的作用，如物流仓储中的货物搬运、工业生产线上的物料配送、家居环境下的智能服务等。而路径规划作为移动机器人的关键技术之一，直接关系到机器人能否高效、安全、精准地完成任务。

一、路径规划的内涵与重要性

路径规划旨在给定机器人所处环境的地图信息、起始点和目标点的位置，为机器人设计出一条从起始点到目标点满足特定优化条件的运动路径。这些优化条件通常包括路径最短、时间耗费最少、能量消耗最低以及尽量避开障碍物等。合理的路径规划可使机器人提高工作效率、减少碰撞风险、延长续航能力，是机器人智能化运行的基石。

二、常见的路径规划方法

（一）基于图搜索的方法 1. A*算法：这是一种广泛应用的启发式搜索算法，它综合运用启发式函数（如欧几里得距离、曼哈顿距离等估计值）对搜索空间进行剪枝，引导机器人朝着目标点快速搜索。在搜索过程中，将地图划分为网格形式，每个网格节点赋予相应成本值，机器人通过不断扩展具有最小综合成本（包含从起始点的实际成本与到目标点的启发成本）的节点，直至找到目标点，最终回溯得到最优路径。 2. Dijkstra算法：属于一种广度优先搜索的变体，它以起始点为中心，逐步向外扩散式地搜索。每次迭代找出离起始点距离最近且未确定最短路径的节点，更新与其相邻节点的距离信息，直到所有节点的最短路径都已确定。该算法能保证找到全局最优路径，但计算复杂度相对较高，适用于地图规模较小、对最优性要求严格的场景。

（二）基于采样的方法 1. RRT（快速探索随机树）算法：通过在机器人的配置空间（包含位置、姿态等状态信息）随机采样点，并逐步构建一棵树状结构来连接这些点。起始点作为树的根节点，新采样的点若能与树上已有节点通过一定规则连接（如满足无碰撞条件且距离在一定范围内），则将其加入树中，持续迭代直至采样点落入目标区域附近，最后从树中提取出一条连接起始点与目标点的路径。RRT算法具有快速探索空间的能力，对高维复杂空间适应性强，但得到的路径通常不是最优路径，后期多配合路径优化算法使用。 2. PRRT（渐进最优快速探索随机树）算法：它是在 RRT 算法基础上的改进，在构建树的过程中，不仅关注空间探索，还注重路径的优化。采用一种渐进式的策略，随着采样次数增加，不断对已有路径进行局部优化，使得最终路径逐渐趋近于全局最优，一定程度上弥补了 RRT 算法路径非最优的缺陷。

（三）基于人工势场的方法该方法将机器人运动空间模拟为一个势场，目标点产生引力势场，吸引机器人向其靠近；障碍物产生斥力势场，促使机器人避开。机器人在合力势场的作用下运动，根据所处位置的势场梯度来调整自身运动方向和速度。优点是计算简单、实时性强，能动态响应环境变化；缺点是容易陷入局部最小值，导致机器人在障碍物附近徘徊无法到达目标点，常需要结合其他方法来克服这一问题。

三、实现步骤

1. 环境建模：首先要获取机器人工作环境的信息，常用的建模方式有栅格地图、拓扑地图、几何特征地图等。栅格地图将环境划分为等大小的网格，简单直观，便于标记障碍物位置；拓扑地图侧重于描述环境中不同区域的连接关系；几何特征地图则依据环境中的物体几何形状构建模型，各有优劣，需根据实际场景选择。 2. 路径搜索与生成：依据选定的路径规划算法，在已构建的环境模型中进行搜索操作，生成初始路径。不同算法在搜索策略、效率、路径质量上有所差异，如 A*算法高效且路径较优，RRT 算法快速探索复杂空间但路径需优化等。 3. 路径优化：对于一些非最优路径规划算法得到的路径，或考虑更多优化需求（如降低能耗、提高平滑度）时，需进行路径优化。可采用曲线拟合、局部搜索替换等方法，将初始的折线型路径转化为更平滑、性能更佳的路径，以利于机器人平稳、高效地运动。 4. 实时调整：由于实际环境动态变化，机器人在运动过程中要实时监测环境，一旦发现路径上出现新增障碍物或目标点变动等情况，需及时重新规划路径，确保任务顺利完成。

四、挑战与展望

随着移动机器人应用场景日益复杂，路径规划面临诸多挑战。一方面，复杂环境下如狭窄通道、动态人群中的实时避障与最优路径规划难度增大；另一方面，多机器人协作系统中的路径协调问题亟待解决，既要避免机器人间碰撞，又要实现协同任务。展望未来，融合深度学习、强化学习等前沿技术，有望使机器人具备更强的自主学习与适应能力，根据不同环境自动选择最优路径规划策略，进一步提升移动机器人的智能化水平。你可以根据具体需求对上述内容进行调整，比如增加特定算法的应用案例、深入阐述某一环节等。

📚2 运行结果

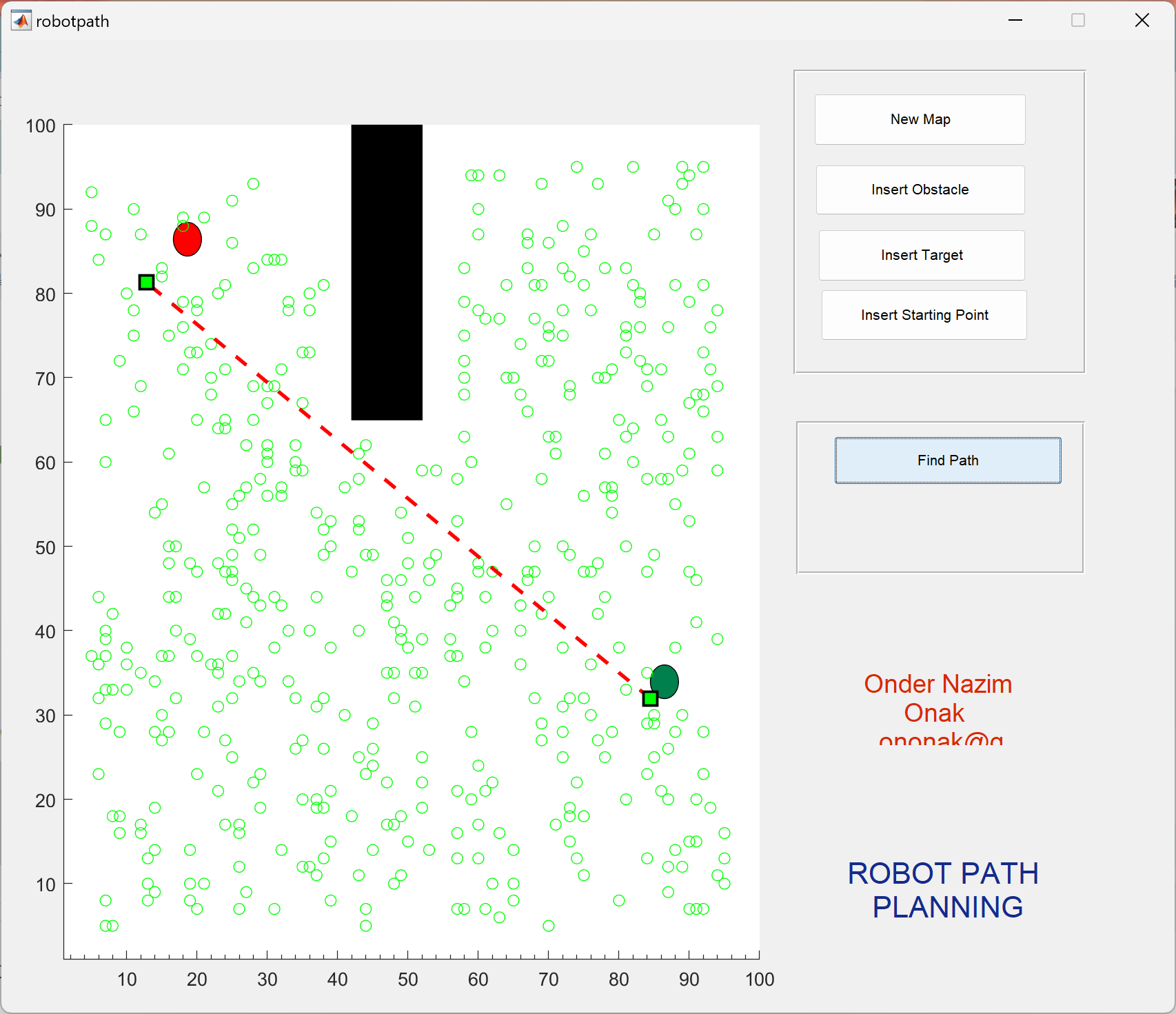
部分函数代码：

function [Cost BestSol] = artificial_bee_colony(map, Vxy)

%% Problem Definition

CostFunction=@(x) ComputeCost(x);        % Cost Function

nVar=2;             

VarSize=[1 nVar];   
VarMin= 5;         
VarMax= 95;         

%% ABC Settings

MaxIt=10;              

nPop=500;               

nOnlooker=nPop;         

L=round(0.6*nVar*nPop); 

a=1;                    

%% Initialization

% Empty Bee Structure
empty_bee.Position=[];
empty_bee.Cost=[];

% Initialize Population Array
pop=repmat(empty_bee,nPop,1);

% Initialize Best Solution Ever Found
BestSol.Cost=inf;

% Create Initial Population
for i=1:nPop
    pop(i).Position=Vxy(i,:); 
    DD = pop(i).Position;
    pop(i).Cost=CostFunction(pop(i).Position);
    if pop(i).Cost<=BestSol.Cost
        BestSol=pop(i);
    end
end

% Abandonment Counter
C=zeros(nPop,1);

% Array to Hold Best Cost Values
BestCost=zeros(MaxIt,1);

%% ABC Main Loop

for it=1:MaxIt