【滤波器】粒子滤波器、Sigma点滤波器以及扩展线性卡尔曼滤波器工具包（Matlab实现）

荧光Matlab

已于 2025-01-20 21:40:07 修改

阅读量1k

点赞数 26

CC 4.0 BY-SA版权

文章标签： matlab 开发语言

于 2025-01-20 21:30:53 首次发布

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/145269691

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

粒子滤波器工具包

粒子滤波器（Particle Filter，PF）是一种基于蒙特卡洛方法的滤波器，适用于处理非线性、非高斯系统的状态估计问题。粒子滤波器工具包通常包含以下主要功能和特点：原理基础：通过随机采样的粒子集合来近似系统状态的概率分布。每个粒子代表系统的一个可能状态，其权值反映了该状态出现的可能性。随着新的观测数据到来，粒子的权值会根据观测模型和状态转移模型进行更新，通过重采样等操作，去除权值低的粒子，保留权值高的粒子，从而实现对系统状态的动态估计。功能模块：一般包括粒子初始化模块，用于根据先验知识生成初始粒子集合；状态预测模块，依据系统状态转移方程预测粒子的下一时刻状态；观测更新模块，根据观测数据计算粒子的权值；重采样模块，对粒子进行筛选和复制，以保持粒子的有效性和多样性。应用场景：广泛应用于目标跟踪、机器人定位与导航、生物医学信号处理等领域。例如在无人驾驶中，可用于车辆对周围环境中目标物体的位置和运动状态的实时跟踪。优势与挑战：优势在于对非线性、非高斯问题的处理能力强，理论上可以逼近任何复杂的概率分布。但缺点是计算量较大，当粒子数量不足时可能出现粒子退化现象，导致估计精度下降。

Sigma点滤波器工具包

Sigma点滤波器（Sigma Point Filter，SPF）是一类用于处理非线性系统滤波问题的方法，主要包括无味卡尔曼滤波器（Unscented Kalman Filter，UKF）等。其工具包具有以下特点：原理基础：基于Sigma点采样策略，通过选择一组特定的Sigma点来近似系统状态的概率分布。这些Sigma点经过非线性系统的传播后，能够更准确地捕捉概率分布的特性，然后通过加权求和等方式计算状态的均值和协方差，实现对系统状态的估计。功能模块：通常有Sigma点生成模块，负责根据系统状态的维度和协方差等信息生成合适的Sigma点；状态传播模块，将Sigma点代入非线性系统模型进行传播；估计更新模块，结合观测数据对状态估计进行更新，计算新的均值和协方差。应用场景：在航空航天、惯性导航、卫星定位等领域有重要应用。比如在飞行器的姿态估计中，能够利用传感器数据准确地估计飞行器的姿态角等状态参数。优势与挑战：相比扩展卡尔曼滤波器，对非线性系统的逼近效果更好，在一定程度上能够提高估计精度，且不需要计算复杂的雅克比矩阵。但计算量相对较大，对系统模型的依赖性较强，模型不准确时可能影响估计效果。

扩展线性卡尔曼滤波器工具包

扩展卡尔曼滤波器（Extended Kalman Filter，EKF）是卡尔曼滤波器在非线性系统中的扩展。其工具包有以下要点：原理基础：通过对非线性系统进行线性化近似，将非线性问题转化为线性问题来处理。具体是利用泰勒级数展开，在当前状态估计值附近对非线性函数进行一阶线性化，然后基于线性卡尔曼滤波器的框架进行状态预测和更新。功能模块：包含线性化模块，用于对非线性的状态转移方程和观测方程进行线性化处理；状态预测模块和观测更新模块与标准卡尔曼滤波器类似，但在计算中考虑了线性化后的系数矩阵。应用场景：常用于机器人运动控制、电力系统状态估计、通信系统中的信号估计等领域。例如在机器人的路径规划中，可根据传感器测量数据估计机器人的位置和速度等状态，为路径规划提供依据。优势与挑战：实现相对简单，在一定程度上能够处理非线性问题，在许多实际应用中取得了较好的效果。然而，其性能依赖于线性化的精度，对于强非线性系统，线性化误差可能较大，导致估计不准确甚至滤波器发散。这三种滤波器工具包在不同的应用场景下各有优劣，在实际使用中，需要根据具体的系统特性、精度要求、计算资源等因素选择合适的滤波器工具包，并对其进行适当的参数调整和优化，以实现最优的状态估计效果。

📚2 运行结果

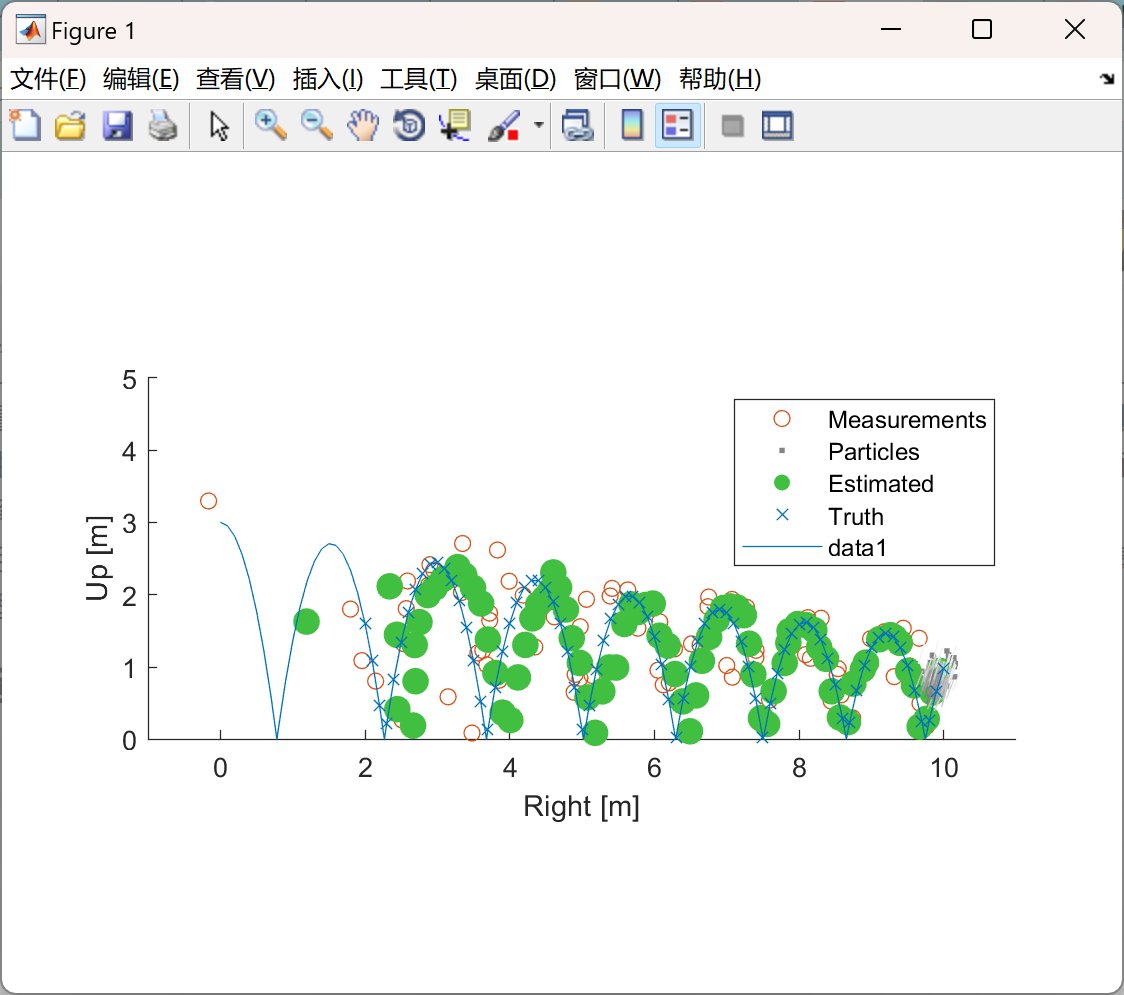
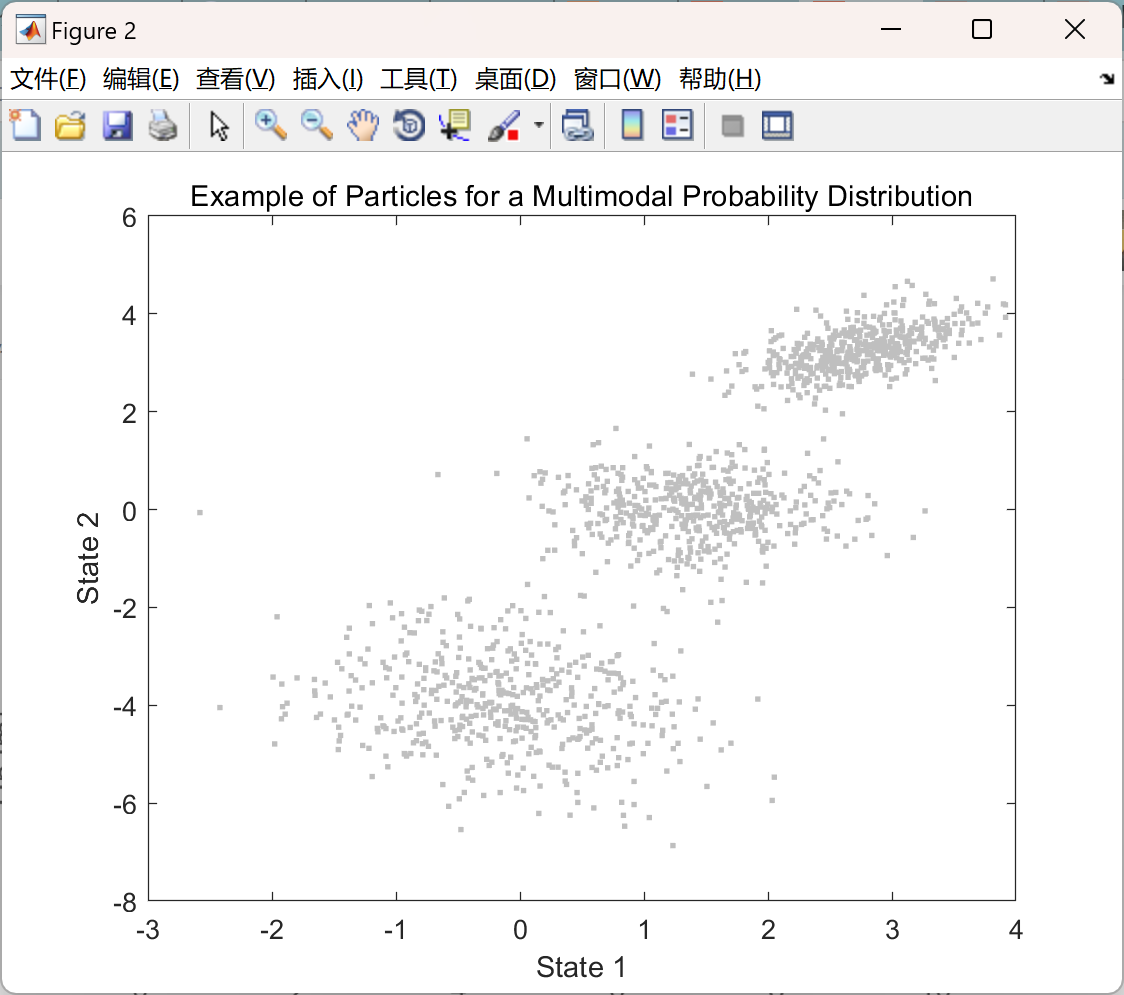
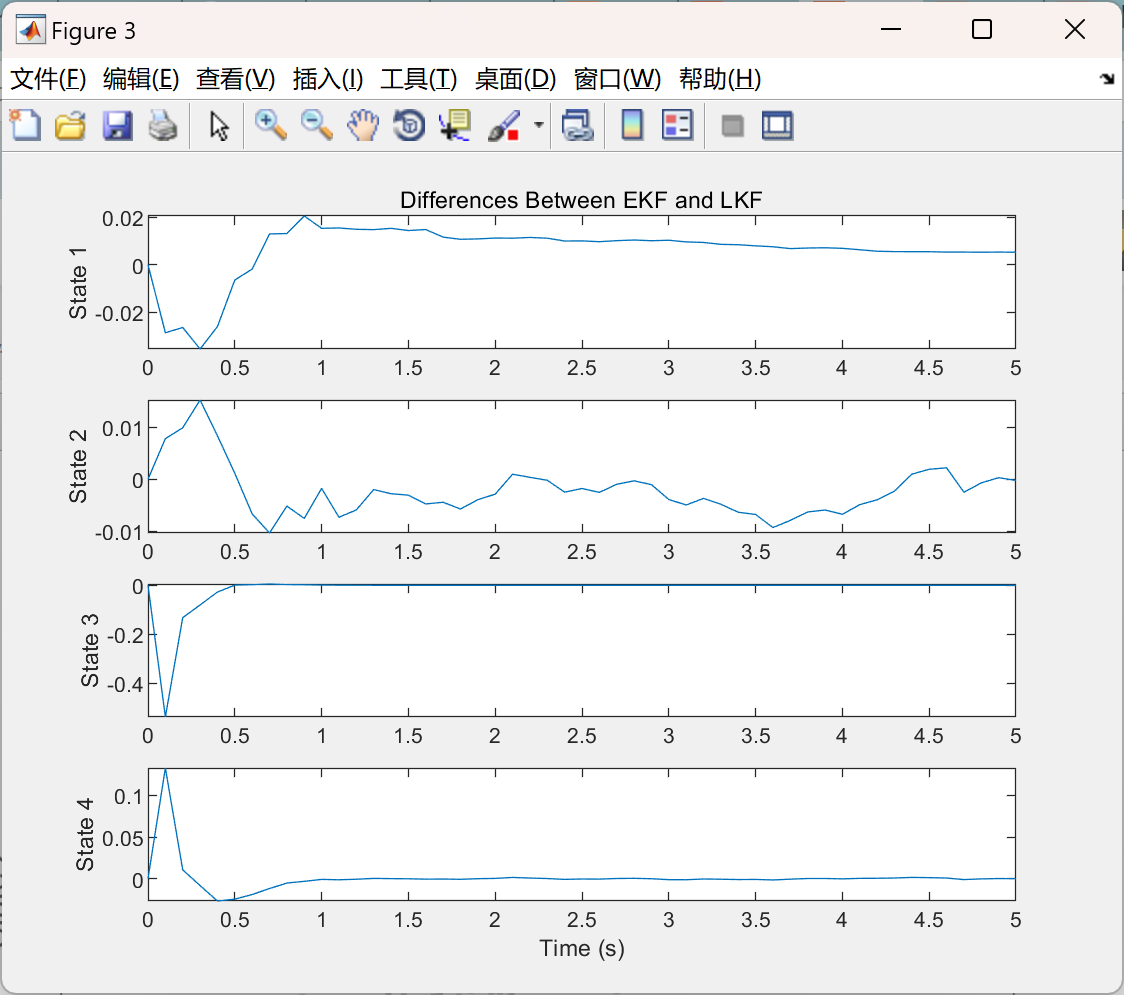
部分函数代码：

rng(1);

% Initial true state, measurement noise covariance, and measurement
x0 = [0; 3; 1; 0];
R  = 0.25^2 * eye(2);
z0 = x0(1:2) + covdraw(R);

% Initial state estimate and covariance. The initial particles will be
% centered on this initial estimate and distributed according to the
% covariance. The initial particle weights are all equal (1/N).
xh0 = [z0; 1; 0];
P0  = blkdiag(R, 2^2 * eye(2));
nX  = 100;
X   = bsxfun(@plus, covdraw(P0, nX), xh0);
w   = 1/nX * ones(1, nX);

% Calculate the whole true trajectory.
[~, x, t] = propagate_ball(0, 10, x0);

% Create a function to calculate the colors for the particles according to
% their weights. This looks pretty good.
colors = @(w) 1 - max(0.95*w/max(w).^0.85, 0.05);

% Prepare the figure.
set(clf(figure(1)), 'Color', [1 1 1]);
colormap('gray');
axis equal;
axis([-1 11 0 5]);
caxis([0 1]);
xlabel('Right [m]');
ylabel('Up [m]');
hold on;

% Add the initial particles.
hX = scatter(X(1,:), X(2,:), [], colors(w), '.');

% Measurement
hz = plot(z0(1), z0(2), 'o', 'Color', [0.85 0.325 0.098]);

% Start the legend.
legend([hz hX], 'Measurement', 'Particles');
% colorbar();

%% Propagate the truth and draw the measurement.

% Manually propagate the truth and take a noisy measurement.
tk = 1;
xk = propagate_ball(0, tk, x0);
zk = xk(1:2) + covdraw(R);
set(hz, 'XData', [get(hz, 'XData'), zk(1)], ...
        'YData', [get(hz, 'YData'), zk(2)]);

%% Propagate the particles, drawing their trajectories.

% Get trajectories for each ball.
xt = cell(1, nX);
Xn = zeros(size(X));
ht = zeros(1, nX);
line_colors = colors(w).' * [1 1 1];
for k = 1:nX
    [Xn(:,k), xt{k}] = propagate_ball(0, 1, X(:,k));
    ht(k) = plot(xt{k}(1,:), xt{k}(2,:), 'Color', line_colors(k,:));
end
set(hX, 'XData', Xn(1,:), 'YData', Xn(2,:), 'CData', colors(w));
uistack(hz, 'top');

%% Show distance to each particle.

hd = zeros(1, nX);
for k = 1:nX
    hd(k) = plot([xt{k}(1,end) zk(1)], [xt{k}(2,end), zk(2)], ...
                 'Color', [0.85 0.325 0.098]);
end

%% Use the bootstrap filter to update the weights.

% Get rid of the error lines.
delete(hd);

% Create the propagation and observation functions.
f = @propagate_ball;
h = @(t, x, u) x(1:2);

% Create a function to make a random process noise draw. Since we don't use
% process noise for the bouncing ball, this is pretty easy:
d = @(varargin) [];

% Create a function to determine how likely a measurement error is. Since
% our measurement errors are Gaussian, we'll use the probability density
% function for a multivariate Gaussian distribution. (Note, since the
% "probabilities" of each particle are only important relative to each
% other, we can drop the constant scaling factor of the PDF.)
invR = inv(R);