【滤波器】自动检测带通滤波器的截止频率（Matlab实现）-优快云博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

在电子信号处理领域，带通滤波器起着至关重要的作用，它允许特定频率范围（通带）内的信号通过，而衰减其他频率（阻带）的信号。其中，截止频率作为带通滤波器的关键参数，精准地界定了通带与阻带的边界，自动检测带通滤波器的截止频率对于滤波器性能评估、系统调试以及众多相关应用有着不可或缺的意义。

一、截止频率的定义与重要性

截止频率通常指信号幅度衰减到某一特定比例（如 -3dB）时对应的频率值。对于带通滤波器，有下限截止频率和上限截止频率，它们共同限定了通带宽度，决定了滤波器能够通过的频率区间。准确知晓截止频率，一方面能确保滤波器按设计要求筛选出所需频率的信号，满足如通信系统中对特定频段信号的提取或降噪应用中对干扰频率的阻隔；另一方面，在滤波器设计与优化阶段，精确的截止频率检测可为调整电路参数提供依据，以实现理想的滤波效果。

二、传统检测方法

扫频法：这是较为经典的方法，利用信号发生器产生一系列不同频率的正弦波信号输入到带通滤波器，同时使用示波器或频谱分析仪等测量设备观察滤波器输出信号的幅度变化。当输出信号幅度下降到设定阈值（对应 -3dB 衰减）时，此时输入信号的频率即为截止频率。扫频法原理直观易懂，但操作相对繁琐，需要人工手动调整信号发生器频率并记录测量结果，耗时较长，且对于一些实时性要求高的系统不太适用。

基于波特图的方法：通过搭建测试电路，测量带通滤波器在不同频率下的增益（或衰减），并绘制波特图（频率 - 增益图）。从波特图中，依据增益下降到指定阈值的转折点来确定截止频率。这种方法能较为全面地反映滤波器在不同频率段的性能，但绘制波特图需要较多的测量数据和一定的绘图技巧，对测试人员要求较高，并且在复杂电路环境下，测量误差可能累积影响截止频率判断的准确性。

三、自动检测技术原理与实现

基于软件算法的自动检测：利用数字信号处理（DSP）算法，将滤波器输出的离散数字信号采集后进行分析。例如，采用快速傅里叶变换（FFT）算法把时域信号转换为频域信号，然后在频域内搜索幅度衰减符合截止频率定义的频率点。该方法结合微处理器或数字信号处理器（DSP 芯片），可实现自动化检测，速度快、精度较高，适用于现代数字化电子系统。一些智能音频处理设备，通过内置 DSP 芯片运行 FFT 算法实时检测音频带通滤波器截止频率，优化声音效果。

利用专用仪器的自动检测：随着电子测量技术发展，出现了如矢量网络分析仪等专业仪器。将带通滤波器接入仪器，仪器自动发射扫频信号并测量滤波器的散射参数（如 S21 表示传输系数），依据 S21 幅度衰减特性快速、精确地自动检测出截止频率，还能同时给出滤波器的其他多项性能参数。这种方式检测效率极高，精度堪称顶级，但仪器价格昂贵，通常用于高端科研、军工等对滤波器性能要求苛刻的领域。

四、面临的挑战与发展趋势

高频与宽带滤波器检测难题：在毫米波、太赫兹等高频段以及超宽带滤波器应用场景下，信号传输特性复杂，传统检测方法受限于测量设备带宽、采样率等因素，难以精准检测截止频率；同时，高频段电磁干扰严重，会影响测量准确性。未来需研发适应高频、宽带的新型检测技术与设备，如基于光子学的测量方法有望突破传统电学测量瓶颈。

实时性与动态适应要求：在一些动态变化的系统中，如自适应通信系统、可穿戴医疗监测设备，滤波器截止频率需要根据工况实时调整，这要求检测技术具备快速动态响应能力，能够实时跟踪滤波器性能变化。采用人工智能结合实时 DSP 算法的方案有望满足此类需求，通过对大量工况数据的学习，智能预测与检测滤波器实时截止频率，保障系统稳定高效运行。

📚2 运行结果

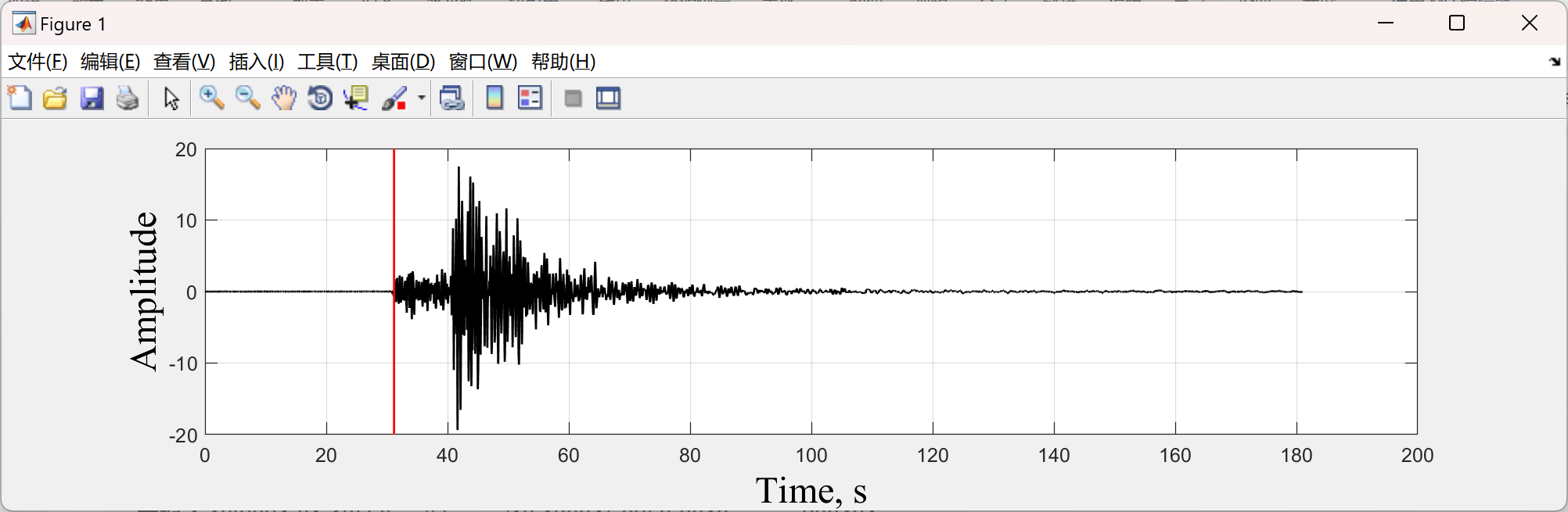
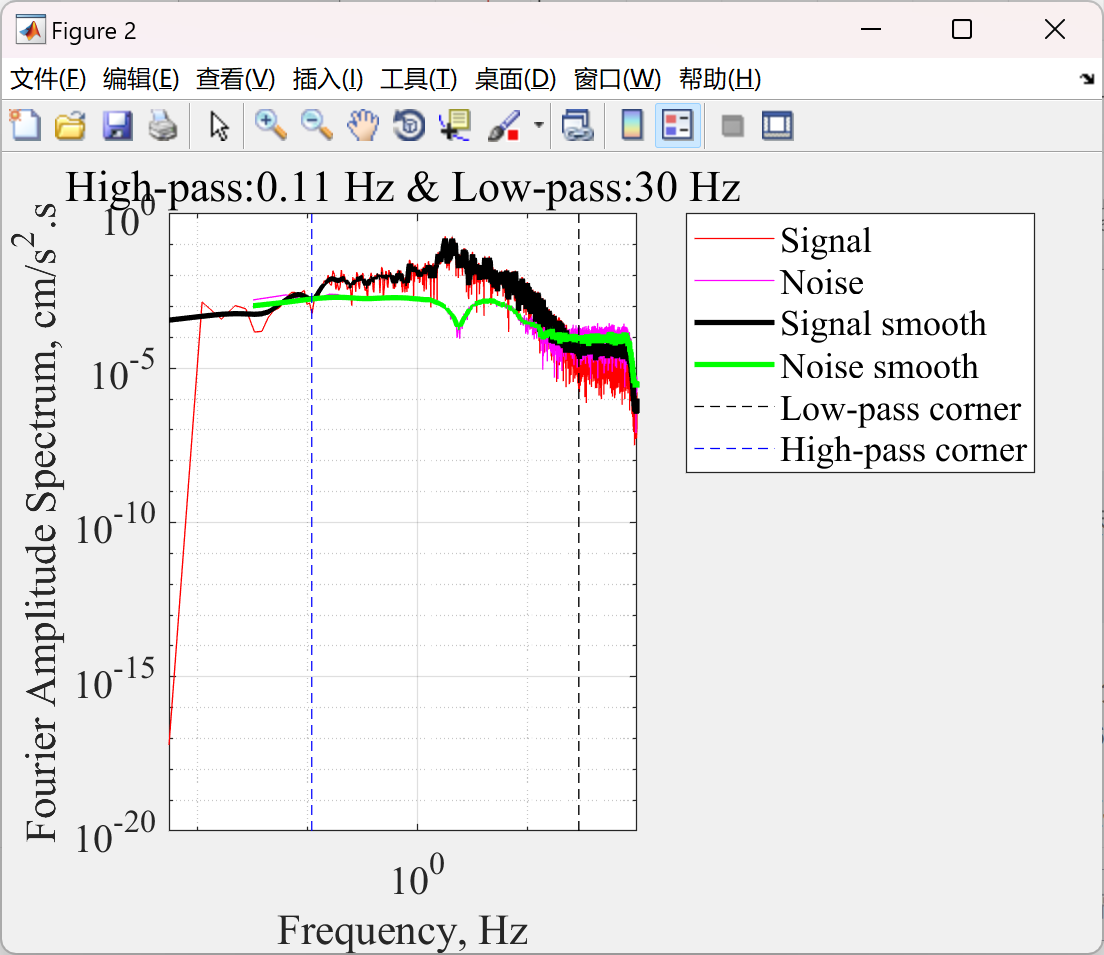
部分函数代码：

function [smoothFAS]=smoothSpectra(Y,varargin)

%% DEFAULT PROPERTIES
if (nargin >= 1)
    w = 40;
    b = 20;
    method = 'konno-ohmachi';
    debug = 'False';
else
    error('smoothSpectra: First argument must be a waveform')
end

%% USER-DEFINED PROPERTIES
if (nargin > 1)
    v = varargin;
    nv = nargin-1;
    if ~rem(nv,2) == 0
        error(['smoothSpectra: Arguments after time series must ',...
            'appear in property name/val pairs'])
    end
    for n = 1:2:nv-1
        name = lower(v{n});
        val = v{n+1};
        switch name
            case 'w'
                w = val;
            case 'debug'
                debug = val;
            case 'b'
                b = val;
            case 'method'
                method = val;
            otherwise
                error('smoothSpectra: Property name not recognized')
        end
    end
end

%% DEBUG OPTION
if strcmp(debug,'True')
        fprintf('applied window .....%s\n', method);
        fprintf('window width .......%d\n', w);
    if strcmp(method, 'konno-ohmachi')
        fprintf('b value ............%d\n', b);
    end
end

%% MAIN
% enforce window width as odd number
if mod(w,2) == 0
    w = w - 1;
end

halfw = round(w/2);

switch lower(method)
    case 'boxcar'
        W = boxcar(w);
    case 'gaussian'
        W = gausswin(w);
    case 'hamming'
        W = hamming(w);
    case 'hann'
        W = hann(w);
    case 'hanning'
        W = hanning(w);
    case 'konno-ohmachi'
        W = (sin(b * log10((1:w)/halfw))./(b*log10((1:w)/halfw))).^ 4;
        % enforce window function to be 1 at central value, which is halfw
        W(halfw) = 1;
    case 'parzen'
        W = parzenwin(w);