【雷达成像】基于成像目标的RF线圈优化（Matlab实现）

原创已于 2024-11-09 14:54:56 修改 · 842 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

于 2024-11-07 11:34:10 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、引言：

射频（RF）线圈在成像技术中起着至关重要的作用。随着科技的不断发展，对成像质量的要求日益提高，基于成像目标进行 RF 线圈优化成为关键课题。

二、RF 线圈在成像中的重要性： RF 线圈负责发射射频信号以激发成像目标，并接收来自目标的反馈信号。其性能直接影响着成像的分辨率、信噪比和对比度等关键指标。不同的成像目标，如人体组织、工业材料等，对 RF 线圈的要求各不相同。

三、基于成像目标的优化需求： 1. 对于人体成像，需要考虑人体不同部位的形状、大小和组织特性，优化 RF 线圈以实现更均匀的信号激发和接收，减少伪影，提高图像质量，同时确保安全性和舒适性。 2. 在工业成像中，针对不同的材料和检测目标，RF 线圈需进行优化以适应复杂的几何形状和材料特性，提高检测的准确性和可靠性。

四、优化方法： 1. 线圈设计优化：通过调整线圈的几何形状、尺寸、匝数等参数，以实现更好的磁场分布和信号耦合。例如，采用多通道线圈设计、异形线圈等。 2. 材料选择与优化：选择合适的导电材料和绝缘材料，以提高线圈的性能和耐用性。同时，考虑材料的电磁特性对成像的影响。 3. 数值模拟与优化算法：利用有限元分析等数值模拟方法，对不同设计方案进行模拟和评估。结合优化算法，如遗传算法、粒子群优化等，自动搜索最优的线圈设计参数。

五、应用与展望：基于成像目标的 RF 线圈优化在医学成像、工业检测、材料科学等领域具有广泛的应用前景。未来，随着技术的不断进步，RF 线圈优化将更加智能化、精准化，为成像技术的发展提供更强大的支持。

📚2 运行结果

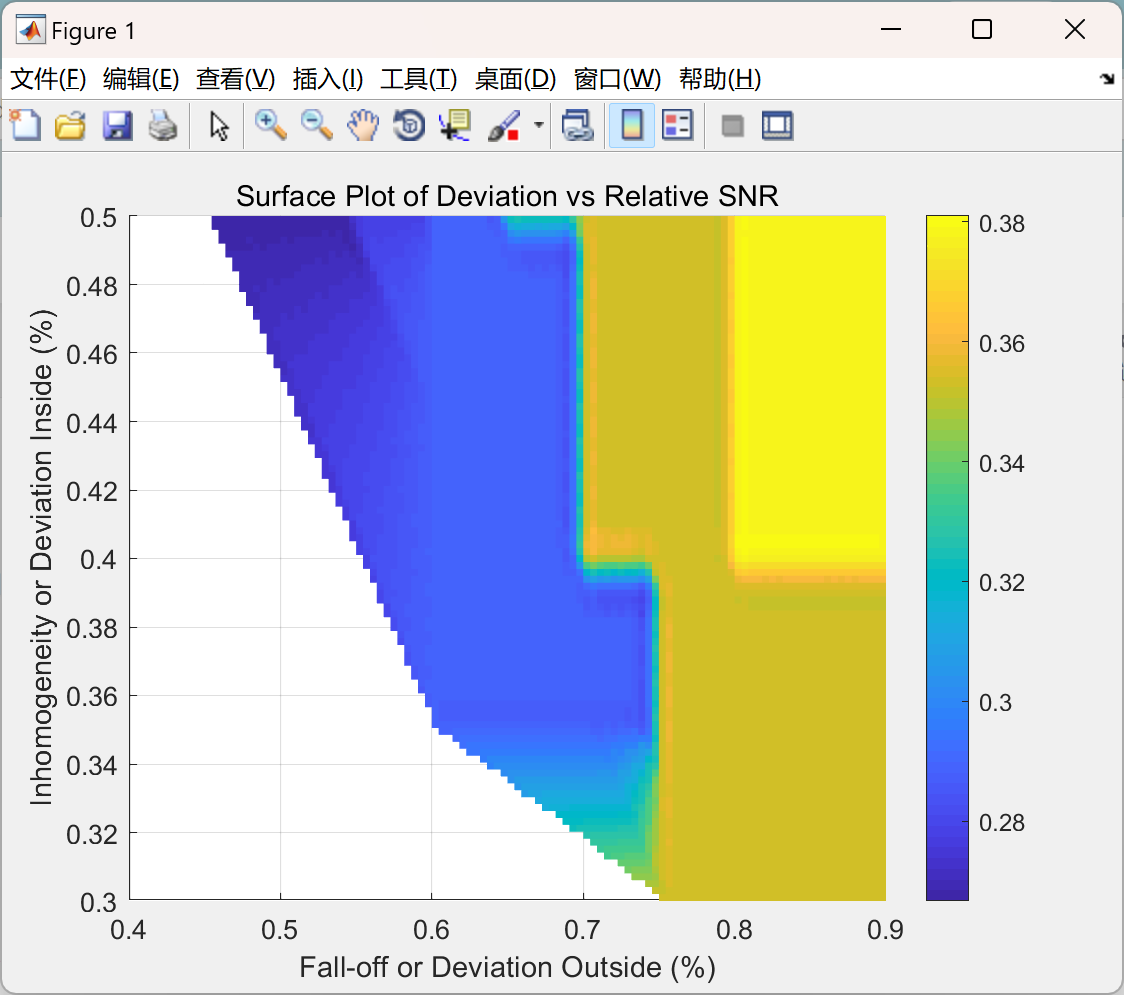
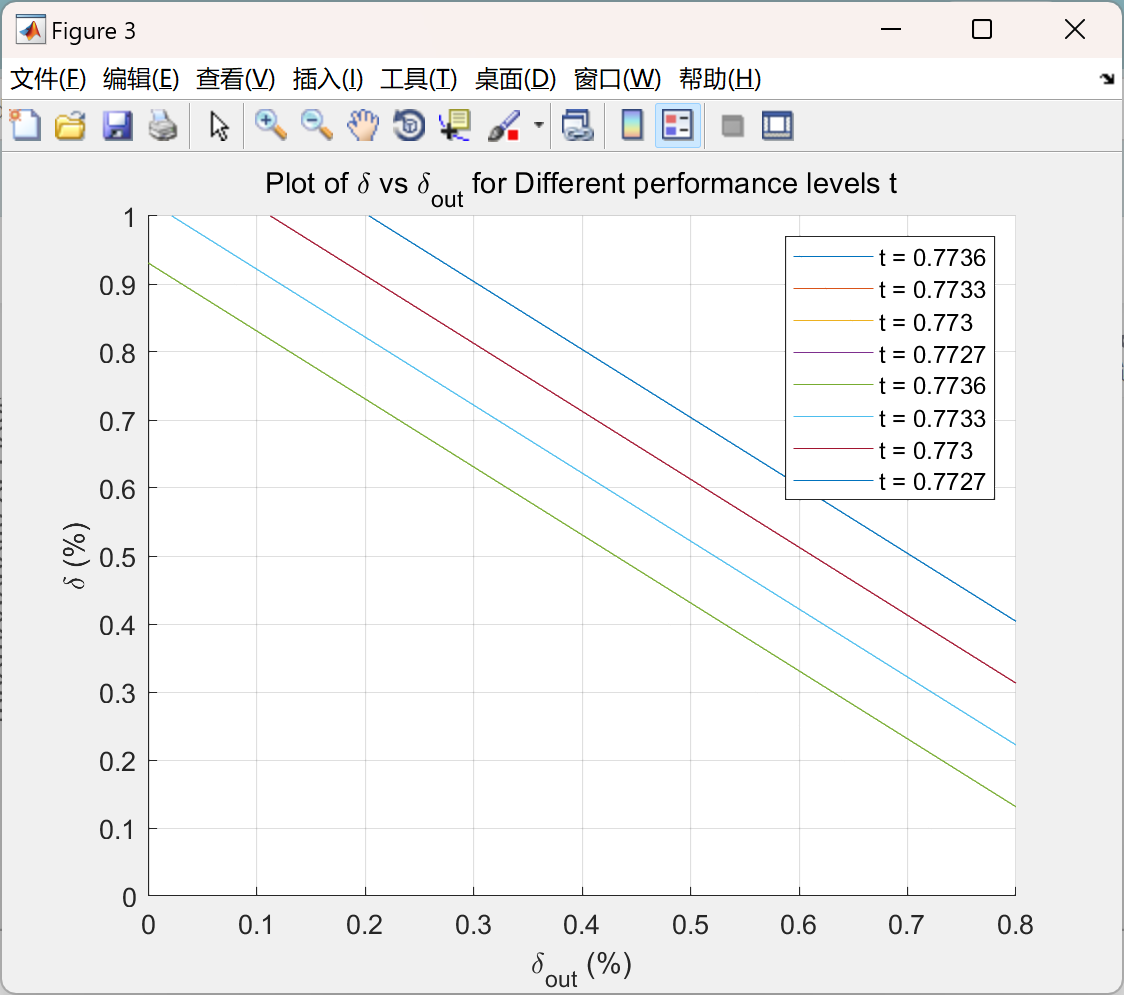
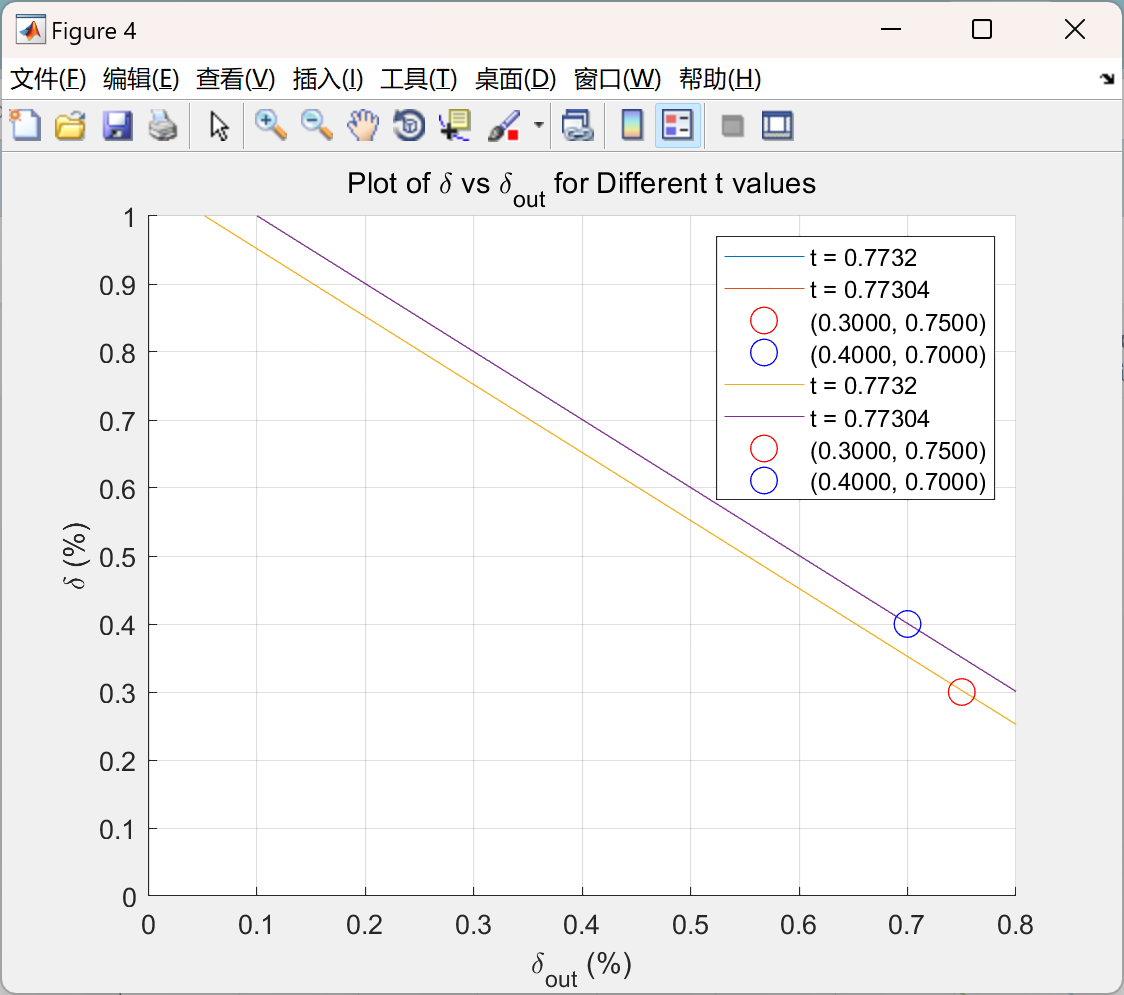
主函数部分代码：

%% Number of grooves and evaluation points

n_grooves = 5;    % Number of grooves
n_inside = 10;    % Evaluation points inside the coil
n_outside = 5;    % Evaluation points outside the coil (chest wall)

%% Desired magnetic field strength and allowed deviations

Bav = 1;                  % Desired magnetic field strength/estimate can be obtained from uniformly wound coil for instance
delta_inside = 0.3 * Bav;  % Maximum allowed deviation inside the coil (30%)
delta_outside = 0.9 * Bav; % Maximum allowed deviation outside the coil (90%)/fall off inside the chest-wall

%% Wire lengths for each groove

groove_lengths = [4, 6, 8, 10, 12]; % for instance from tip to bottom of coil

%% Define A matrix based on values obtained from Maxwell-FEM simulations

% Inside matrix (10 rows, 5 columns)
% Each column represents the produced B-fields of one groove
% Each row represents the produced B-fields at one evaluation point inside
% the coil volume (produced by the different grooves)

A_inside = [
    0.8, 0.5, 0.3, 0.2, 0.1; 
    0.75,0.55,0.45, 0.35, 0.15; 
    0.7, 0.6, 0.4, 0.3, 0.2;
    0.6, 0.6, 0.4, 0.3, 0.2; 
    0.5, 0.7, 0.5, 0.4, 0.3; 
    0.4, 0.5, 0.6, 0.5, 0.3; 
    0.35, 0.45, 0.55, 0.6, 0.4;
    0.3, 0.4, 0.5, 0.7, 0.5; 
    0.2, 0.3, 0.4, 0.6, 0.6; 
    0.1, 0.2, 0.3, 0.5, 0.7; 
];

% Outside matrix (5 rows, 5 columns)
% Each column represents the produced B-fields of one groove
% Each row represents the produced B-fields at one evaluation point outside
% the coil volume (produced by all grooves)
A_outside = [
    0.1, 0.2, 0.3, 0.5, 0.6; 
    0.1, 0.2, 0.3, 0.5, 0.5; 
    0.05, 0.15, 0.25, 0.4, 0.4; 
    0.05, 0.1, 0.2, 0.3, 0.35; 
    0.0, 0.05, 0.15, 0.2, 0.25
];

% Ensure that A_inside and A_outside have the correct number of rows
disp(['A_inside size: ', num2str(size(A_inside))]);  % Should be [10, 5]
disp(['A_outside size: ', num2str(size(A_outside))]); % Should be [5, 5]

%% Set up the constraints (inside and outside the coil)

rhs_inside_min = (Bav - delta_inside) * ones(n_inside, 1);  % Lower bound for inside the coil
rhs_inside_max = (Bav + delta_inside) * ones(n_inside, 1);  % Upper bound for inside the coil
rhs_outside_min = (Bav - delta_outside) * ones(n_outside, 1);  % Lower bound for outside the coil
rhs_outside_max = (Bav + delta_outside) * ones(n_outside, 1);  % Upper bound for outside the coil

%% Combine the constraints (inside and outside)